Для построения статической модели диода, полные ВАХ диода представляют отрезками прямых так, чтобы они с наибольшей точностью аппроксимировали реальную характеристику в заданном конкретном режиме эксплуатации (в рабочем диапазоне тока и напряжения). Аппроксимирующие отрезки прямых можно провести касательными к|до| реальной характеристике (см. рис. 1.3).
Рисунок 1.3 – кусково-линейная аппроксимация ВАХ диода
Разделим реальную ВАХ диода с помощью касательных на три области:
– область проводимости 
: 
;
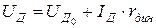– область отсечения 
: 
;
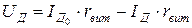– область пробоя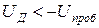 
: 
.
Каждой из выделенных областей ВАХ можно поставить в соответствие статические модели диодов в виде электрических схем замещения (см.рис.1.4). Непосредственно из рисунка| видно, что наибольшая погрешность моделей приходится на области стыковки прямых.
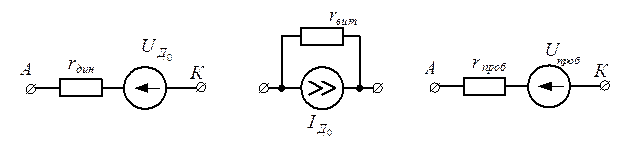
Рисунок 1.4 – кусково-линейные модели диода
Биполярный транзистор
Следующим не менее распространенным элементом схемы является биполярный транзистор. Схема нелинейной инжекционной модели идеализированного транзистора структуры р-п-р, предложенная Эберсом и Моллом, приведена на рисунке 1.5
Рисунок 1.5 - Схема нелинейной инжекционной модели идеализированного транзистора
В общем случае токи эмиттера и коллектора определяются следующим образом:
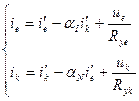, (1.3)
где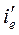 
и 
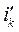- токи эмиттерного и коллекторного переходов, определяемые по модели (1.1);
, 
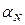- коэффициенты обратной и прямой передачи тока транзистора с общей базой;
, 
- сопротивления утечки соответственно эмиттерного и коллекторного переходов.
На основании моделей (1.1) и (1.3) можно записать:
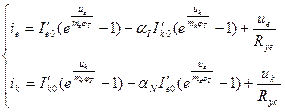, (1.4)
где 
, 
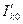- токи насыщения переходов, определяемые аналогично току 
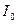из уравнения (1.1).
Эти токи могут быть выражены через паспортные данные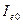 
и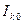 
, измеряемые соответственно при обрыве коллектора и эмиттера:
и 
. (1.5)
Коэффициенты обратной и прямой передачи тока транзистора с общим эмиттером или общим коллектором обозначаются через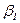 
и 
, которые связаны с коэффициентами и 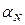следующими соотношениям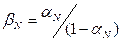и:
и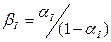 
. (1.6)
Практическая нелинейная статическая модель транзистора, как и для диода, дополняется слагаемыми, учитывающими сопротивления в толщине полупроводникового материала.
Математическая модель в этом случае принимает следующий вид:
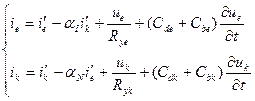. (1.7)
При анализе электронных схем, содержащих нелинейные элементы, используется кусочно-линейная аппроксимация, которая основана на замене отдельных участков характеристики 
отрезками прямых линий. Точки излома кусочно-линейной характеристики 
располагаются так, чтобы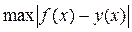 
были минимальны на каждом интервале линейного приближения. Кусочно-линейное представление характеристик элементов используется для получения кусочно-линейных эквивалентных схем замещения. Так, в случае аппроксимации вольт-амперной характеристики нелинейного элемента координате 
соответствует напряжение 
, а координате 
- ток 
и кусочно-линейная схема замещения представляется схемой, состоящей из линейного резистивного элемента и источника постоянного тока или напряжения (рисунок 1.6).
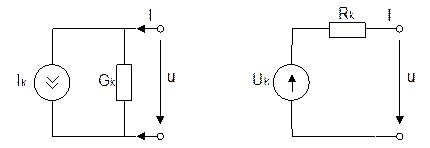
а) б)
Рисунок 1.6 - Кусочно-линейная схема замещения нелинейного элемента
Аппроксимации ВАХ нелинейных элементов, управляемых напряжением соответствует схема замещения, приведенная на рисунке 1.6 а, состоящая из источника тока с задающим током 
и линейной проводимости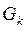 
:
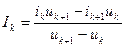; (1.8)
. (1.9)
Аппроксимации ВАХ нелинейных элементов, управляемых током соответствует схема замещения, приведенная на рисунке 1.6б, состоящая из источника напряжения Uk и линейного сопротивления Rk:
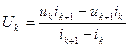; (1.10)
. (1.11)
Таким образом, структура кусочно-линейной схемы замещения элемента будет неизменной для всех интервалов аппроксимации, т.е. для всех режимов работы цепи. Переход от одного линейного участка к другому приводит лишь к изменениям величин параметров линейного резистивного элемента и источника.