Пусть некоторая схема содержит (п+1), включая базисный. В схеме присутствуют источники тока, линейные проводимости и нелинейные двухполюсные резистивные элементы, управляемые напряжением, т.е. такие, токи которых 
являются однозначными функциями напряжения 
.
, (2.1)
где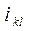 
- ток ветви, включенной между узлами k и λ;
- напряжение ветви, включенной между узлами k и λ;
- нелинейная проводимость элемента;
- узловые напряжения;
Полагая, что в общем случае нелинейный источник тока, управляемый напряжением 
включен между узлами p и q.
, (2.2)
Запишем уравнения по первому закону Кирхгофа для узлов k, λ, p и q.
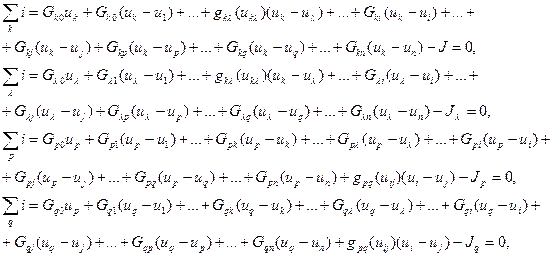(2.3)
где Gst - проводимости линейных ветвей,
Jk,Jλ,JP,Jq- токи независимых источников.
Сгруппировав соответствующие слагаемые, перепишем модель (2.3) в матричной форме:
(2.4)
где
Из полученного уравнения видно, что нелинейные проводимости, так же, как и проводимости линейных двухполюсников входят в матрицу проводимостей четыре раза, из них два раза с положительными знаками в собственные проводимости узлов k и λ, а два - с отрицательными во взаимные проводимости этих узлов. Нелинейная проводимость gpq(uij) преобразования ПНТ, вход которого подключен к узлам i и j, авыход - к узлам р и q, также входит в матрицу проводимостей четыре раза. Два раза без инверсии знака во взаимные проводимости Ypi и Yqj и два раза с инверсией - в проводимости YPJ и Yqi. Заметим, что линейные и нелинейные проводимости ветвей, соединяющих узел s сбазисным, входят в матрицу проводимости один раз с положительным знаком, в собственную проводимость узла Yss. Передаточная проводимость ПНТ, вход которого включен между узлом f и базисным, а выход - между узлом r и базисным, также входит в матрицу проводимостей один раз, без инверсии знака, в проводимость Yrf.
При формировании вектора независимых источников I ток JK λ источника, направленного от узла k к узлу λ, прибавляется к элементу λ, вектора I и вычитается из элемента k.
Для исключения сингулярности матрицы коэффициентов, имеющей место при ик λ =0, выделим из матрицы коэффициентов уравнений (2.4) матрицу постоянных коэффициентов G и матрицу коэффициентов, зависящих от переменных g(U), тогда уравнения (2.4) можно переписать в виде:
G-U + Ф(U) -I= 0, (2.5)
где Ф(U) - вектор нелинейных функций
Вектор функций Ф(U)может быть получен без использования матрицы g(U),если рассматривать нелинейные элементы, как эквиваленные источники тока 
. В этом случае вектор функций формируется аналогично вектору I независимых источников, т.е.
.
В общем случае анализа статического режима возникает ряд трудностей:
1). кроме резистивных элементов, управляемых напряжением, схема содержит элементы, управляемые током, т.е. такие, напряжения которых являются однозначными функциями токов;
2). в схеме могут присутствовать независимые или управляемые
источники напряжения.
В первом случае резистивный элемент, управляемый током описывается уравнением
(2.6)
из которого следует
(2.7)
Функция 
обычно не имеет обратного преобразования с функцией 
в модели (2.1), поэтому значение тока 
в модели (2.3) остается неизвестным и для получения совместной системы уравнений к п уравнениям (2.4) добавим уравнение (2.7). С учетом очевидного соотношения ik = - 
= , матрица коэффициентов увеличится на одну строку и один столбец, а векторы неизвестных и независимых источников на один элемент:
(2.8)
При наличии m таких нелинейных элементов и линейных сопротивлений матрица коэффициентов будет состоять из четырех блок-матриц:
1) матрицы узловых проводимостей Y размером п х п для элементов,
допускающих описание в форме линейной проводимости или управляемой
напряжением нелинейной проводимости;
2) диагональной матрицы R размером т х т сопротивлений
линейных элементов или управляемых током нелинейных сопротивлений;
3) матрицы инциденций А размером п х т, каждый i-ый столбец
которой содержит один или два ненулевых элемента в строках,
соответствующих узлам k и λ, (один из них может быть базисным) подключения i-го сопротивления. Причем ненулевой элемент равен «+1», если ток направлен от узла, и «-1» в противном случае;
4) транспонированной матрицы инциденций Ат.
Векторы неизвестных, независимых источников и нулевой вектор соответственно дополняются т неизвестными токами и т нулями.
Во-вторых, можно ввести дополнительную переменную – ток 
в ветви с источником напряжения, учесть его в уравнениях (2.4) для узлов k и λ и добавить к системе уравнений компонентное уравнение 
В результате матрица коэффициентов увеличивается на одну строку и один столбец, а векторы неизвестных и независимых источников - на один элемент.
(2.9)
В таблице 2.3 источника [5] приведены модифицированные системы узловых уравнений для управляемых источников, у которых матрица у-параметров не существует.