ЧАСТЬ 3. Распространение радиоволн
Глава 7. Дифракция и рефракция электромагнитных волн
7.1. Содержание, постановка и методы решения задач
Дифракции
Задача возбуждения электромагнитных волн сторонними источниками в свободном пространстве была рассмотрена в первой части курса [1]. Если в пространстве находятся какие-либо материальные объекты, то процесс распространения электромагнитных волн существенно отличается от рассмотренного ранее, и возникает задача о возбуждении этих объектов, т.е. задача отыскания вторичных полей как вне, так и внутри объектов – полей дифракции.
Рассмотрим основные понятия и определения, связанные с явлениями дифракции, а также некоторые методы решения дифракционных задач.
Поля дифракции
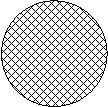
При возбуждении какого-либо материального объекта (а – диэлектрическое тело, б – проводящее тело, в – отверстие в проводящем экране, рис. 7.1.) некоторой падающей на него волной, поля которой (
, 
) полагаются известными, возникают поля дифракции.
 | |||
 | |||
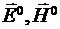
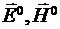
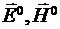
(а) (б) (в)
Рис.7.1. Дифракция на различных объектах
- 5 -
Поле внутри диэлектрического тела (
, 
) называется внутренним полем дифракции. Вне объектов появляется внешнее поле дифракции (
, 
), которое в случаях «а » и «б » можно назвать отраженными, а в случае «в » внешнее поле дифракции складывается из отраженного (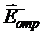
, 
) (над экраном) и прошедшего (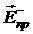
, 
) (под экраном) полей. В общем случае внешнее поле дифракции называется полем рассеяния.
Заметим, что к классу дифракционных задач можно отнести и задачу о возбуждении плоской границы раздела двух сред, подробно рассмотренную во второй части пособия [2].
Для нахождения внешнего и внутреннего полей дифракции необходимо решить соответствующую граничную задачу, т.е. найти решение однородной системы уравнений электродинамики [1], которое удовлетворяет граничным условиям:
на поверхности диэлектрического объекта
, (7.1)
,
на поверхности идеально проводящего объекта
; 
. (7.2)
Кроме того внешнее поле дифракции должно удовлетворять условию излучения на бесконечности [1].
Методы решения задач дифракции
При решении задач дифракции в большинстве случаев получить строгое решение, т.е. представить в явном виде формулами, в которые входят исходные данные задачи, не удается. Лишь в некоторых случаях (например, дифракция на шаре, бесконечном цилиндре), можно получить строгое решение задачи и поля представить рядами, в которых коэффициенты разложения определяются непосредственно из граничных условий на поверхности объекта.
Практически интересные для высокочастотной радиотехники, в том числе для радиолокации, дифракционные задачи связаны с объектами сложной геометрической формы.
- 6 -
Для решения таких задач существуют и развиваются универсальные приближенные численные методы с использованием интегральных уравнений электродинамики и проекционных методов.Библиография по этим вопросам частично приведена в [3]. На базе этих методов возможно построение алгоритмов и программ для решения сложных дифракционных задач с помощью ЭВМ (в том числе персональных компьютеров).
При отыскании приближенного решения дифракционной задачи обычно используется некоторый малый параметр, в качестве которого можно взять отношение характерного размера объекта 
(например, его длины или периметра) к длине волны 
(или обратной величины 
).
При этом различают три области решения:
1. Квазистационарная область (длинноволновое приближение). При этом малый параметр задачи 
<< 
( 
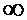) и волновое число 
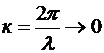. Волновое уравнение Гельмгольца преобразуется в уравнение Лапласа, описывающее статические (стационарные) поля.
2. Резонансная область (параметр 
) наиболее сложна для исследования. Для решения используются строгие методы (метод собственных функций, метод интегральных уравнений).
3. Квазиоптическая область (коротковолновое приближение). При этом малый параметр задачи 
(
).
Чем меньше 
, тем более точные результаты в этой области дает геометрическая оптика. Однако, при этом фронт волны и поверхность объекта должны быть локально плоскими.
Квазиоптические методы решения подразделяются на две группы:
1. Асимптотические методы. Они основаны на исследовании точных решений при стремлении .
2. Эвристические (интуитивные) методы с привлечением некоторых физических идей. Сюда относятся:
А) Лучевые методы – геометрическая оптика и ее уточнения.
Б) Волновые методы – физическая оптика (приближение
- 7 -
Кирхгофа) и ее уточнения.