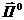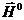Дифракция ПОВ на отверстии в экране

Рассмотрим нормальное падение ПОВ из полупространства на про­водящий экран с отверстием произвольной формы (рис.7.6.).

Падающая ПОВ имеет составляющие:

, . (7.26)

Ограничиваясь исследованием внешнего поля дифракции лишь в по­лупространстве за экраном , в приближении Кирхгофа счи­таем, что на теневой стороне экрана, обращенной в это полупространство,

поля равны нулю , а в раскрыве отверстия равны

- 15 -

неискаженному полю падающей ПОВ:

; . (7.27)

y

S z

x So P

0

Q

Рис. 7.6. Падение ПОВ на отверстие в экране

Можно считать, что эти поля (или соответствующие им эквивалент­ные поверхностные токи) в каждой точке отверстия образуют ис­точник излучения в пространство в виде элемента Гюйгенса, и, таким образом, внешнее поле дифракции в произвольной точке наблюдения определяются суммарным излуче­нием всех элементов Гюйгенса, находящихся в раскрыве отверстия .

В сферической системе координат 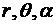электрическое поле каждого элемента Гюйгенса, занимающего элемент поверхности раскрыва отверстия , в дальней зоне () определяется выражением [1]:

. (7.28)

Так как на практике размеры отверстия много меньше расстояния до точек дальней зоны, то из всех этих точек отверстие видно практически под нулевым углом, а любой элемент Гюйгенса, находящийся в отверстии,

дает одинаковую зависимость поля от координат и . Поэтому при опреде­лении суммарного поля в точке наблюдения интегрированием выраже -

- 16 -

ния (7.28) по площади от­верстия из-под знака интеграла можно вынести функции координат и . В итоге получаем:

, (7.29)

где (7.30)

Расстояние элемента Гюйгенса, находящегося в точке , до точки наблюдения определяется выражением:

, (7.31)

где - расстояние от начала координат до точки наблюде­ния.

С учетом соотношений , разлагая в степенной ряд и оставляя в разложении первые три слагаемых, получаем::

. (7.32)

Если расстояние настолько велико, что при вычислении 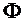(7.30) слагаемое 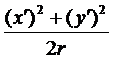в выражении (7.32) практически не влияет на фазу 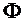и им можно пренебречь, то, как говорят, имеет место дифракция Фраунгофера.

При этом слагаемое , и в знаменателе подынтегрального выражения (7.30), влияющем на амплитуду поля элемента Гюйгенса, можно положить 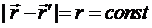и вынести из-под знака интеграла. В показателе экспоненты такое допущение не корректно, так как фаза подынтегрального выражения может существенно меняться от точки к точке в раскрыве отверстия (особенно, когда размеры отверстия соизмеримы или больше длины волны ).

- 17 -

С учетом сказанного выражение (7.30) принимает вид:

. (7.33a)

Рассмотрим прямоугольное от­верстие в экране размером (рис.7.7.).

Рис. 7.7. Прямоугольное отверстие в экране

Используя формулу Эйлера , в результате интегрирова­ния получаем:

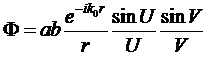, (7.33б)

где , 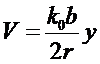. (7.34)

Переходя к сферическим координатам 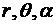(рис. 7.8.) и используя соотношения

; , (7.35)

преобразуем (7.34):

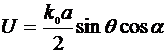, . (7.36)

- 18 -

Рис. 7.8. Прямоугольное отверстие в сферической системе координат

При этом выражение для поля (7.29) принимает вид:

. (7.37)

Полученное выражение показывает, что внешнее поле дифракции в дальней зоне представляет собой сферическую (локально плоскую) неодно­родную волну.

Магнитное поле определяется известным соотношением [1]:

,

которое, с учетом (7.37) и ,

принимает вид:

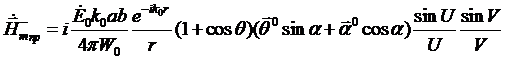. (7.38)