Анализ поля дифракции Фраунгофера

 

Напомним, что в дальней зоне зависимость модуля напряженности

- 19 -

 

поля какого-либо источника от направления в точку наблюдения, т.е. от

углов и , называется диаграммой направленности данного источника излуче­ния. При исследовании диаграммы направленности обычно делается нормировка по максимальному значению поля.

Диаграмму направленности прямоугольного отверстия в экране удобно рассматривать в двух плоскостях:

1. при ( - плоскость) – для составляющей ,

2. при ( - плоскость) – для составляющей .

В первом случае легко показать, что

,

и нормированная диаграмма направленности с учетом, что , описывается выражением:

(7.39)

Аналогично во втором случае имеем: ,

,

и нормированная диаграмма направленности описывается выраже­нием:

. (7.40)

В формулах (7.39), (7.40) первый множитель представляет собой нормированную диаграмму направленности элемента Гюйгенса, а второй учитывает распределение элементов Гюйгенса в отверстии по координатам и , соответственно, и называется интерференционным множителем.

Диаграмма направленности имеет многолепестковую структуру с главным максимумом излучения в направлении .

- 20 -

 

В частном случае, когда размеры отверстия велики по сравнению с длиной волны , в области малых углов первые мно­жители в формулах (7.39), (7.40) , и диаграмму направленности фактически определяют интерференционные множители. Поэтому можно полагать, что:

, (7.41)

. (7.42)

Графически функция представлена на рис. 7.9а., а соответствую­щая ей диаграмма направленности в полярной системе координат - на рис. 7.9 б.

Определим ширину главного лепестка диаграммы направленности в - плоскости как угол между ближайшими направлениями и , в которых излучение отсутствует.

Из рис.7.9а следует, что нулевому уровню главного лепестка диаграм­мы направленности в направлении (рис.7.9 б.) соответствует первый корень функции . При этом, с учетом (7.41), угол определяется из следующего уравнения:

. (7.43)

Отсюда получаем: , а .

Для отверстия, у которого , можно считать, что , и ­

ширина главного лепестка диаграммы направленности “по нулям” в

 

- 21 –

 

-плос­ко­сти определяется выражением:

. (7.44)

а

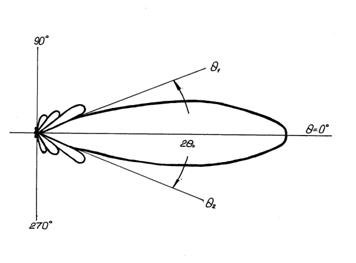
б.

Рис. 7.9. Диаграмма направленности прямоугольного отверстия

 

Аналогично, если 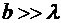, то ширина главного лепестка диаграммы на­прав­ленности “по нулям” в - плоскости определяется выражением:

(7.45)

Отметим, что при увеличении размеров отверстия и (или) уменьшении длины волны из (7.44),(7.45) следует, что ширина главного лепестка

диаграммы направленности сужается. При этом, если , то резуль-

тат соответствует приближению геометрической оптики.

- 22 -

Основные понятия геометрической оптики

На весьма высоких частотах, когда производные по времени от функ­циональных представлений электромагнитного поля волны существенно больше производных по координатам, делается предположение о локально плоском характере поля волны, что приводит к геометрооптической лучевой трактовке процесса распространения волны.

Эта концепция широко используется при рассмотрении многих задач дифракции, а также задач рефракции - распространения электромагнитных волн в неоднородном пространстве, в том числе таких, как распространение земных, тропосферных и ионосферных волн, о которых пойдет речь в следующей главе.

 

Уравнение эйконала

Предположим, что на большом расстоянии от источников в неоднород­ной среде с параметрами , 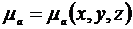распростра­няется волна, электромагнитное поле которой определяется вы­ражениями: , , (7.46)

где - постоянная распространения в вакууме;

- некоторая скалярная функция, физический смысл которой рассмотрим ниже;

, - вектора, составляющие которых в зависимости от координат изменяются значительно медленнее, чем от времени.

Подставляя эти выражения полей в первое уравнение Максвелла

и используя соотношение векторного анализа:

 

,

получаем:

 

- 23 -

 

В этом выражении очень велико, поэтому, пренебрегая первым слагаемым, получаем:

(7.47)

где , - волновое сопротивление вакуума.

Подставляя (7.46) во второе уравнение Максвелла, аналогично пре­дыдущему получаем:

, (7.48)

где .

Из выражений (7.47), (7.48) следует, что вектора образуют правовинтовую ортогональную тройку.

 

Подставляя из (7.47) в (7.48), получаем:

 

, (7.49) где - коэффициент преломления среды.

Применяя к (7.49) соотношение векторного анализа:

 

,

 

с учетом, что , получаем так называе­мое уравнение эйконала (от греческого эйкон - изображение):

, (7.50)
или

, (7.51)
где - единичный вектор (лучевой орт).

Уравнение эйконала (7.50) в развернутой форме:

 

- 24 -

 

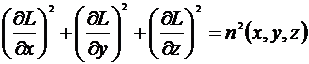(7.52)

представляет собой нелинейное дифференциальное уравнение в частных производных первого порядка. Оно является основным соотношением гео­метрической оптики неоднородных сред.

Вектор Пойнтинга, определяющий направление движения энергии, ~ показывает, что энергия волны движется вдоль .

Из выражений (7.47), (7.51) вытекает соотношение:

,

где - волновое сопротивле­ние пространства.

Таким образом, в геометрооптическом приближении поле в каждой точке пространства носит характер плоской однородной волны, распро­страняющейся в направлении .

 

Уравнение луча

Значения определяет эквифазную поверхность – фронт волны.

Семейство линий, ортогональных к эквифазным поверхностям, назы­вается лучами.

По определению перпендикулярен эквифазной поверхности , поэтому направление луча в каждой точке пространства совпа­дает с направлением или .

В общем случае неоднородной среды эквифазные поверхности пред­ставляют собой изогнутые поверхности, а лучи – пространственные кривые, т.е. имеет место процесс непрерывного преломления (рефракция) электро­магнитной волны.

Выведем уравнение луча, исходя из геометрии, представленной на рис. 7.10., где показана лишь одна координатная ось .

- 25 -

 

x

 

Рис. 7.10. К выводу уравнения луча

 

Здесь - единичный вектор, касательный к в каж­дой точке пространства; , , , где a, b, g - на­правляю­щие углы .

По определению луча .

- радиус-вектор текущей точки на луче.

Рассмотрим производную:

(7.53)

Отсюда уравнение эйконала можно записать в виде:

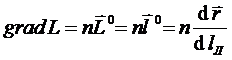. (7.54)

Дифференцируя (7.54) слева и справа по , получаем:

- 26 -

 

. (7.55)

Из приведенных выкладок, в частности, следует, что или
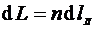, т.е. элемент длины пути равен элементу геометрического пути вдоль луча d 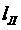, умноженному на коэффициент преломления среды . В оптике принято называть оптической длиной пути.

Таким образом, дифференциальное уравнение луча второго порядка в векторной форме имеет вид:

(7.56)

 

В частном случае однородной среды () имеем:

, т.е.

; ; ,

и луч представляет собой прямую линию.

При этом , и функция, определяющая изменение фазы поля волны, принимает вид:

 

7.4.3. Радиус кривизны луча

В общем случае уравнение луча (7.56) описывает пространственную кривую, в каждой точке которой можно определить ее радиус кривизны , являющийся важным параметром при практических расчетах тропосферных линий связи, о которых будет идти речь в следующей главе.

Рассмотрим на луче точки a и b, расстояние между которыми

(рис.7.11.).

Единичный вектор в точке b получает приращение . Можно

 

- 27 -

считать, что длина дуги ab , откуда получаем:

 

. (7.57)

a Луч

b

 

a

a

Рис. 7.11. К определению радиуса кривизны луча

 

Введем векторную характеристику кривизны луча:

, (7.58)

где единичный вектор направлен вдоль противоположно выпуклости луча, и будем считать , если выпуклость направлена от центра кривизны в точке 0.

В соответствии с (7.53) перепишем уравнение луча (7.56) в виде , и, вычисляя производную слева с учетом, что по определению , получаем:

. (7.59)

 

- 28 -

 

Рассмотрим распространение электромагнитной волны в среде, коэффициент преломления которой зависит лишь от координаты z, т.е. на поверхности уровня , а .

Определим радиус кривизны луча (траектории движения волны) в точке q, где его направление образует с и с произвольный угол (рис. 7.12а.).

z z z

Луч2 Луч2

Луч

Луч1 q

q

Луч1

q

0 0 0

а б в

Рис. 7.12. Траектории движения волны.

 

При этом выражение (7.59) преобразуется к виду:

, откуда

 

. (7.60)

Подставляя (7.60) в (7.58), получаем:

. (7.61)

Отсюда, возведя левую и правую части в квадрат, находим:

 

. (7.62)

- 29 -

 

Знак “минус” в (7.62) учитывает, что при (плотность среды уменьшается с ростом z) радиус кривизны (луч 1), а при (плотность среды увеличивается с ростом z) радиус кривизны (луч 2).

Если луч идет вдоль положительного направления оси z () перпендикулярно поверхности уровня , то из (7.62) находим, что в любом случае (, либо , либо ) , т.е. луч представляет собой прямую линию, параллельную оси z (рис.7.12б). Если луч идет вдоль отрицательного направления оси z (), то аналогично получаем .

Если луч идет вдоль поверхности уровня (), то радиус кривизны определяется выражением . В этом случае, если , то (луч 1), а если , то (луч 2)

(рис.7.12в.).

Для протяженных тропосферных линий связи (см. раздел 8.3.2.), полагая, что , , радиус кривизны луча можно рассчитывать по формуле:

. (7.63)

 

Принцип Ферма

Уравнение эйконала (7.51) проинтегрируем слева и справа по произ­вольной кривой между точками и (рис. 7.13.):

(7.64)

 

 

- 30 -

 

Луч

l

B

A

 

 

Рис. 7.13. К выводу принципа Ферма

 

С учетом того, что

,

а ,

вычисление интеграла слева дает:

. (7.65)

Таким образом, интеграл слева не зависит от формы пути .

Интеграл справа

, (7.66)

где - угол между направлением луча и единичным вектором касательной 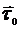к пути интегрирования .

Приравнивая (7.65) и (7.66), получаем:

(7.67)

Если путь интегрирования совпадает с направлением луча 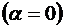, то

(7.68)

Этот интеграл называется оптической длиной пути вдоль луча.

Из (7.68) следует, что оптическая длина пути вдоль луча между двумя эквифаз­ными поверхностями всегда одна и та же, хотя геометрические длины пути могут быть различными (рис. 7.14.).

- 31 -

Рис. 7.14. Оптические и геометрические длины пути между

эквифазными поверхностями

 

Из формул (7.67), (7.68) вытекает равенство

,

которое с учетом, что , преобразуется в соотношение:

. (7.69)

Это неравенство выражает широко используемый в оптике принцип Ферма, который гласит, что оптическая длина пути между двумя точками пространства минимальна, если путь идет по лучу.

 

* * *

В заключение кратко обозначим границы применимости метода геометриче­ской оптики при решении задач дифракции и рефракции.

1.Метод можно применять, если параметры среды , и амплитуда

поля мало изменяются на расстояниях, равных длине волны в среде.

2.Метод можно применять, если кривизна поверхности объекта и фронта падающей волны мало меняются на расстоянии, равном длине волны, т.е. рассматриваемый случай близок к задаче о падении плоской волны на бесконечную плоскость.

3. Метод не применим в зоне тени, где геометрическая оптика дает чис­тый ноль поля, и в области полутени, где она дает разрыв поля на границе “свет – тень”.