В общем случае при падении ПОВ (
, 
) на цилиндрический объект возникают внешнее (
, 
) и внутреннее (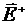
, 
) поля дифракции, причем на всей поверхности объекта, включая торцы (если цилиндр конечный), должны выполнятся граничные условия (7.1), (7.2). Наиболее просто эти граничные условия записать для объекта в виде бесконечного однородного кругового цилиндра с параметрами 
, 
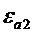, находящегося в среде с параметрами 
, 
, поверхность которого совпадает в цилиндрической системе координат 
, 
, 
с координатной поверхностью 
(рис.7.2.)
z
y
III
I II 
0 a r x
2 а
Рис. 7.2 Дифракция ПОВ на цилиндре
Комплексные амплитуды поля ПОВ, поляризованной вдоль оси цилиндра и движущейся вдоль координаты 
,представляются в виде:
; 
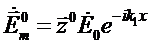, (7.3)
- 8 -
где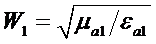 
- волновое сопротивление пространства I.
Для удовлетворения граничным условиям на поверхности цилиндра внешние и внутренние поля дифракции должны быть однородными по оси . Однородные волновые уравнения Гельмгольца для составляющих 
этих полей в цилиндрической системе координат имеет вид:
, (7.4)
где индекс 
.
Поля дифракции периодичны по координате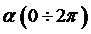 
, поэтому их можно представить в виде рядов Фурье по системе функций 
:
(7.5)
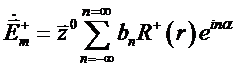(7.6)
где 
- неизвестные функции распределения полей по координате 
,
- неизвестные амплитудные коэффициенты,
Подставляя (7.5), (7.6) в (7.4), получаем уравнение Бесселя относительно функции :
(7.7)
Его решением являются цилиндрические функции 
-ого порядка:
-функция Бесселя; 
- функция Неймана.
Линейные комбинации этих функций также представляют решения уравнения Бесселя:
- 9 -
функция Ханкеля 1-го рода - 
, (7.8)
функция Ханкеля 2-го рода - 
. (7.9)
Внутреннее поле дифракции должно быть конечным, поэтому в его представлении (7.6) в качестве 
нужно использовать конечные в начале координат функции Бесселя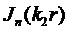 
.
Внешнее поле дифракции (7.5) необходимо представлять через функцию Ханкеля 2-го рода 
, которая при 
описывает расходящуюся волну, удовлетворяющую условию излучения на бесконечности [3].
Экспоненту 
, входящую в выражения (7.3) для поля падающей ПОВ, также можно представить в виде ряда Фурье по системе функций 
:
, (7.10)
где 
- коэффициенты разложения Фурье.
При этом поле падающей ПОВ записывается в форме, аналогичной (7.5), (7.6):
, (7.11)
и его можно трактовать как бесконечную сумму так называемых цилиндрических гармоник, каждая из которых удовлетворяет однородному волновому уравнению Гельмгольца.
Неизвестные амплитудные коэффициенты гармоник внешнего и внутреннего полей дифракции 
и 
определяются из граничных условий (7.1), которые для электрического поля можно записать в виде:
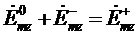при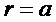 
, (7.12)
- 10 -
откуда получаем:
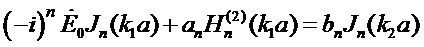. (7.13)
Из второго уравнения Максвелла 
в цилиндрической системе координат находим:
, (7.14)
где 
- волновое сопротивление среды..
Граничное условие для магнитного поля можно записать в виде:
при , (7.15)
откуда с учетом (7.14) получаем:
, (7.16)
где штрих означает производную по полному аргументу.
Решая совместно (7.13) и (7.16), находим:
, (7.17)
. (7.18)
Подставляя (7.17), (7.18) в (7.5), (7.6), находим выражения для электрических полей дифракции, а с помощью второго уравнения Максвелла находим магнитные поля дифракции. Таким образом, строгое решение поставленной задачи получено.
В частном случае дифракции ПОВ на идеально проводящем цилиндре 
, для которого 
, из (7.18) следует, что 
,
- 11 -
т.е. внутреннее поле дифракции отсутствует (электромагнитное поле в идеальный проводник не проникает).
Из (7.17) в этом случае получаем:
, (7.19)
при этом суммарное поле вне цилиндра на конечном расстоянии опре-деляется выражением:
.
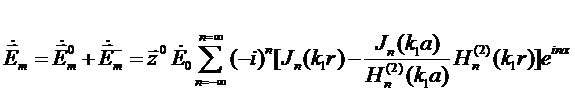(7.20)
Суммарное магнитное поле определяется с помощью второго ура –внения Максвелла. Отметим, что при практических расчетах поля по формуле (7.20) для получения точности ~ 1 % необходимо учитывать 
членов ряда.