Уравнение неразрывности потока

В. В. Богачев

 

 

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

РАБОТЫНАГНЕТАТЕЛЕЙ

 

Учебное пособие

(курс лекций)

 

Ставрополь

Издательство СевКавГТУ

УДК

ББК

Б

Рецензенты:

 

Богачев, В. В.

Б Теоретические основы работы нагнетателей: учебное пособие (курс лекций) / В. В. Богачев. – Ставрополь: СевКавГТУ, 2010. – 82 с.

 

 

УДК

ББК

 

 

© Богачев В. В., 2010 © ГОУВПО «Северо-Кавказский государственный технический университет», 2010

СОДЕРЖАНИЕ

 

 

ВВЕДЕНИЕ................................................................................................... 5

 

ЛЕКЦИЯ 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕХНИЧЕСКОЙ МЕХАНИКИ ЖИДКОСТЕЙ. ПАРАМЕТРЫРАБОТЫНАГНЕТАТЕЛЕЙ..................... 6

1.1. Уравнение неразрывности потока......................................................... 6

1.2. Уравнение движения............................................................................... 7

1.3. Гидравлические сопротивления............................................................. 10

Контрольные вопросы.................................................................................. 12

 

ЛЕКЦИЯ 2. УРАВНЕНИЕ ЭЙЛЕРА ДЛЯ РАБОТЫЛОПАСТНОГО КОЛЕСА 13

2.1. Уравнение Эйлера для работы лопастного колеса............................... 15

2.2. Характеристики лопастных нагнетателей............................................. 16

Контрольные вопросы.................................................................................. 18

 

ЛЕКЦИЯ 3. ПОТЕРИ ДАВЛЕНИЯ В НАГНЕТАТЕЛЯХ.

ПОДОБИЕ ЛОПАСТНЫХ НАГНЕТАТЕЛЕЙ............................................ 19

3.1. Потери перед рабочим колесом............................................................. 19

3.2. Потери в рабочем колесе....................................................................... 20

3.3. Потери за рабочим колесом................................................................... 21

3.4. Подобие лопастных нагнетателей.......................................................... 27

3.5. Универсальные характеристики............................................................ 29

3.6. Общие характеристики........................................................................... 31

3.7. Безразмерные (отвлеченные) характеристики...................................... 32

Контрольные вопросы.................................................................................. 33

 

ЛЕКЦИЯ 4. РАБОТА НАГНЕТАТЕЛЯ В СЕТИ........................................ 34

4.1. Потери давления в сети.......................................................................... 34

4.2. Работа насоса в сети............................................................................... 37

4.3. Метод наложения характеристик........................................................... 38

4.4. Присоединение нагнетателя к сети......................................................... 39

4.5. Выходные элементы вентиляционных установок................................. 41

Контрольные вопросы.................................................................................. 42

 

ЛЕКЦИЯ 5. СОВМЕСТНАЯ РАБОТА НАГНЕТАТЕЛЕЙ........................ 43

5.1. Параллельное включение нагнетателей................................................. 43

5.2. Методика построения характеристик.................................................... 45

5.3. Последовательное включение нагнетателей.......................................... 48

5.4. Нагнетатели с одинаковой характери­стикой......................................... 50

5.5. Нагнетатели с разными характеристи­ками........................................... 50

Контрольные вопросы.................................................................................. 52

 

ЛЕКЦИЯ 6. ЭКСПЛУАТАЦИОННЫЕ ОСОБЕННОСТИ РАБОТЫНАГНЕТАТЕЛЕЙ В СЕТЯХ........................................................................................................... 53

6.1. Неточность расчета потерь давления в сети.......................................... 53

6.2. Отключение и дросселирование сети..................................................... 54

6.3. Негерметичность сети............................................................................. 55

6.4. Изменение температуры......................................................................... 55

6.5. Перемещение механических примесей.................................................. 57

Контрольные вопросы.................................................................................. 59

 

ЛЕКЦИЯ 7. УСТОЙЧИВОСТЬ РАБОТЫНАГНЕТАТЕЛЕЙ.................... 60

7.1. Возникновение неустойчивых режимов работы................................... 60

7.2. Помпаж................................................................................................... 62

7.3. Кавитация................................................................................................ 63

Контрольные вопросы.................................................................................. 67

 

ЛЕКЦИЯ 8. РЕГУЛИРОВАНИЕ НАГНЕТАТЕЛЕЙ.................................. 68

8.1. Способы регулирования........................................................................ 68

8.2. Дросселирование.................................................................................... 69

8.3. Регулирование перепуском.................................................................... 71

8.4. Изменение частоты вращения рабочего колеса.................................... 72

8.5. Регулирование частоты вращения нагнетателя

с по­мощью гидромуфты................................................................................ 73

8.6. Изменение относительной скорости...................................................... 76

8.7. Закручивание потока перед рабочим колесом...................................... 77

8.8. Осевой направляющий аппарат............................................................. 78

Контрольные вопросы.................................................................................. 80

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ......................................... 81

 

ВВЕДЕНИЕ

ЛЕКЦИЯ 1

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕХНИЧЕСКОЙ МЕХАНИКИ ЖИДКОСТЕЙ. ПАРАМЕТРЫРАБОТЫНАГНЕТАТЕЛЕЙ

Техническая гидроаэромеханика изучает законы движе­ния, относительного покоя и взаимодействия жидкости с твердыми телами, которые либо находятся в ней, либо ее ограничивают. Под жидкостью понимают такую мате­риальную среду, медленная деформация которой при по­стоянном объеме возможна под действием ничтожно ма­лых сил. Жидкости делятся на два класса: малосжимаемые – капельные и сжимаемые – газы. При движении газов со скоростями, значительно меньшими скорости звука, сжимаемостью газа можно пренебречь. В этом случае при исследовании движения газов применяют уравнения движения капельных жидкостей. Техническая механика жидкости базируется на ос­новных законах сохранения массы, энергии и импульса, которые широко применяются в технике.

Уравнение неразрывности потока

Рассмотрим уста­новившееся движение жидкости в канале произвольного сечения (рис. 1.1).

Пусть поток движется со скоростью с от сечения 1 – 1 к сечению 2 – 2.В соответствии с зако­ном сохранения массы вещества та масса жидкости, ко­торая находится между сечениями 1 – 2 и 2 – 2, для рас­сматриваемого случая движения должна быть постоян­ной. Это означает, что масса жидкости, прошедшая че­рез живое сечение канала площадью ω₁ будет равна массе жидкости, прошедшей через живое сечение кана­ла площадью ω₂, т. е.

(1.1)

где ρ₁ и ρ₂ – плотность жидкости, проходящей через сечение 1 – 1и 2 – 2 соответственно.

Выражение (1.1), являясь следствием закона сохра­нения массы, называется уравнением неразрывности по­тока жидкости. Из уравнения неразрывности потока, часто записываемого в виде

(1.2)

следует, что, если предположить существование внутри установившегося потока жидких струек, для каждой из которых должно выполняться условие (1.2), то они нигде не могут закончиться. Эти струйки либо должны простираться от одной границы рассматриваемого про­странства до другой, либо замыкаться. В тех случаях, когда несжимаемые (капельные) жидкости или газы движутся под действием относительно малых перепадов давления и весь поток рассматривается как одна жидкая струйка, произведение ω c = Q называют объемным рас­ходом потока, а произведение ρω c = М – массовым рас­ходом.

Уравнение движения

Известно, что основными си­лами, действующими в движущейся жидкости, являют­ся массовые и поверхностные. Если канал, в котором движется жидкость, является неподвижным, то единст­венной массовой силой, действующей в жидкости, будет вес. К поверхностным силам относится силы гидродина­мического давления и силы трения.

Количественной мерой различных форм движения материи служит понятие, называемое в физике энер­гией. Если тело движется, то оно обладает энергией; если тело обладает энергией, оно может совершить ра­боту, которая в дальнейшем (в соответствии с принци­пами сохранения энергии) может перейти в другую фор­му энергии (например, в тепловую).

Рассмотрим установившееся движение вязкой жидко­сти с учетом ее сжимаемости. Как известно, при движе­нии сжимаемых жидкостей работа сил трения оказыва­ет двоякое действие: с одной стороны, являясь реактив­ной силой, она тормозит поток, действуя в противопо­ложном движению направлении; с другой стороны, рабо­та сил трения, целиком превращаясь в теплоту, возвра­щается в поток в виде тепловой энергии, которая может расходоваться на расширение жидкости и, следователь­но, на ускорение ее движения.

Выделим некоторый объем в трубке тока движущей­ся жидкости и ограничим его сечениями 1 – 1 и 2 – 2(рис. 1.2).

Рассматривая установившееся движение, за­пишем для этого объема уравнение сохранения энергии в следующей формулировке: работа внешних сил плюс подведенная теплота расходуются на изменение механи­ческой и внутренней энергии рабочего тела. Как извест­но, внешними силами, действующими при перемещении жидкости от сечения 1 – 1 к сечению 2 – 2,являются силы давления и силы трения. Пусть за некоторый про­межуток времени под действием сил давления произо­шло перемещение объема жидкости, заключенного меж­ду сечениями 1 – 1 и 2 – 2, в сечения 1’ – 1’ и 2' – 2'.Это означает, что вблизи сечения 1 – 1(см. рис. 1.2) исчез­нет элемент массы

а около сечения 2 – 2 появится равный ему элемент массы

Спроектируем все силы на направление движения массы жидкости. Силы гидродинамического давления, действующие на боковую поверхность выделенного объе­ма, составляющих в направлении движения не дадут, и их работа по перемещению массы жидкости равна нулю. Таким образом, суммарная работа сил давления, под действием которых произошло перемещение жидкоcти из сечения 1 – 1 в сечение 2 – 2, определится выражением:

(1.3)

Обозначим удельную работу сил трения, возникаю­щую в потоке движущейся жидкости при перемещении ее из сечения 1 – 1 в сечение 2 – 2,Δ R. Таким образом, суммарная удельная работа внешних сил, совершаемая при перемещении потока жидкости из сечения 1 – 1 в се­чение 2 – 2,с учетом направления действия этих сил за­пишется в виде p ₁ V ₁ – p ₂ V ₂ – Δ R.

Вследствие работы вязких сил возможный приток теплоты в трубку тока между сечениями 1 – 1 и 2 – 2 будет равен M Δ q, где Δ q – количество теплоты, полу­ченное каждой единицей массы жидкости, прошедшей путь между этими сечениями. Таким образом, Δ q – удельное количество теплоты, поступающей в массу жидкости между сечениями 1 – 1 и 2 – 2.

В соответствии с законом сохранения энергии удель­ные работа внешних сил и подведенная теплота долж­ны привести к изменению удельных механической и внутренней энергий потока жидкости. Удельную внут­реннюю энергию массы жидкости обозначим через U.

Масса жидкости, находящейся между сечениями 1 – 1 и 2 – 2, остается постоянной, поэтому изменение удель­ной энергии при перемещении жидкости из сечения 1 – 1 в сечение 2 – 2определится как разность удельных энер­гий элементов массы dm ₂ и dm ₁. Таким образом, закон сохранения удельной энергии для выделенного элемен­та трубки тока может быть записан в виде

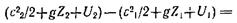
(1.4)

Полученное выражение (1.4) часто используется в дифференциальной форме:

d(c ² / 2 )+gdZ+dU = –d(pv) – d(pv)dR+dq. (1.5)

Уравнение сохранения энергии (1.5) может быть до­полнено уравнением, вытекающим из первого начала термодинамики, согласно которому подведенная к си­стеме теплота увеличивает ее внутреннюю энергию и со­вершает работу расширения, т. е.

dq = dU+pdv. (1.6)

Подставляя выражение (1.6) в уравнение (1.5) и интегрируя имеем выражение

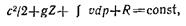
(1.7)

представляющее собой уравнение Д. Бернулли, учиты­вающее как сжимаемость жидкости, так и работу сил трения. Каждый член уравнения (1.7) определяет удель­ную энергию или удельную работу.