Подобие лопастных нагнетателей

Сложность гидро- и аэродинамических процессов, про­исходящих врабочем органе лопастного нагнетателя, делает невозможным расчет его характеристики. Поэто­му она строится только экспериментально. Однако при проектировании нового нагнетателя необходимо иметь такую характеристику для установления его эксплуата­ционных возможностей. Теория подобия позволяет, выб­рав существующий (модельный) нагнетатель, получить размеры рабочего органа проектируемого (натурного) нагнетателя, соответствующие требуемой характеристи­ке. Значительно дешевле бывает (особенно при проек­тировании мощных нагнетателей) изготовить модель существенно меньших размеров и провести ее испы­тания. Теория подобия позволяет, испытав модель про­ектируемого нагнетателя, предсказать рабочие парамет­ры натурного.

Как же сказывается изменение частоты вращения привода и геометрических размеров нагнетателя на его характеристике? Ответ на этот вопрос можно получить с помощью теории гидродинамического подобия, кото­рая утверждает, что две машины будут гидродинами­чески подобны, если для них выполняются три условия.

1. Геометрическое подобие, согласно которому необ­ходимо существование пропорциональности соответст­вующих размеров нагнетателя.

2. Кинематическое подобие, которое предусматривает пропорциональность скоростей в сходственных точках потока.

3. Равенство углов установки лопаток на входе и выходе из рабочего колеса, а также равенство КПД натуры и модели.

Формулы пересчета подачи, давления (напо­ра) и мощности, полученные на основе теории подобия, позволяют пересчитывать параметры, определяющие работу нагнетателей при изменении час­тоты вращения привода л, диаметра рабочего колеса и плотности перемещаемой среды, а также характерис­тики натурных нагнетателей, полученные на модельных установках.

В настоящее время широко применяется метод про­ектирования новых нагнетателей путем пересчета по формулам подобия. Для пользования этим методом не­обходимо разработать параметр, который служил бы критерием подобия и был бы одинаков для всех нагне­тателей. Таким параметром является коэффициент бы­строходности.

Коэффициентом быстроходности n_s называют такую частоту вращения геометрически подобного насоса, ко­торый при напоре Н = 1 мимеет подачу Q = 0,075 м³/с.

Коэффициент быстроходности определяется по уравнению:

(3.3)

где п – частота вращения, мин^-1; Q – подача, м³/с; Н – напор, м.

Коэффициент быстроходности п_s является критерием подобия. Это означает, что если два насоса имеют раз­личные значения п, Q и Н,но одно и то же значение п_s,то они называются подобными.

Конструкции рабочих колес в значительной степени зависят от коэффициента быстроходности n_s. В зависи­мости от его значения рабочие колеса лопастных машин условно разделяют на пять основных типов (рис. 3.6).

При увеличении коэффициента быстроходности на­блюдаются уменьшение относительного наружного диа­метра и увеличение диаметра рабочего колеса. При достаточно большом диаметре рабочее колесо постепен­но преобразуется из радиального (центробежного) в осевое.

На рис. 3.6 также видно, что насосы с высоким ко­эффициентом быстроходности характеризуются относи­тельно низкими подачами и высоким напором, а насо­сы с низким коэффициентом быстроходности, наоборот, характеризуются высокими подачами и низким на­пором.

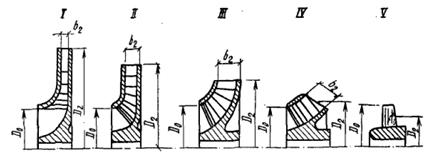
Рисунок 3.6 – Классификация рабочих колес по коэффициенту быстроходности

В практике эксплуатации вентиляторов коэффициент быстроходности n_s принято вычислять по формуле:

(3.4)

где L – подача, м³/с; р – давление, Па; п – частота вращения, мин^-1.

В каталогах приводятся значения п_s, соответствую­щие оптимальному режиму работы нагнетателя. Для ра­диальных вентиляторов n_s = 6 – 110.