Корпус аппарата (рисунок 1.1) является основным узлом, который определяет форму и размеры аппарата, его объем, производительность и очень часто – стои- 
мость. 
Корпус изолирует обрабатываемый в аппарате продукт, подвергаясь его воздействию, воспринимая основные механические и тепловые нагрузки. Надеж- 
ность работы аппарата во многом зависит от правиль- 
ности работы его корпуса. Корпусы аппаратов, чаще всего, изготавливают методом сварки, и состоят они из набора пластин раз- 
личной конфигурации и оболочек вращения – цилинд- 
рических (рисунок 1.1 поз. 1), конических (рисунок 1.1 поз. 2), сферических, эллиптических (рисунок 1.1
поз. 4), торовых (рисунок 1.1 поз. 3) и др.
Упругой оболочкой или пластиной, называется упругое тело, одно из измерений которого (толщина) мало по сравнению с двумя другими. Если тело ис-кривлено, то говорят об оболочке, а если оно плоское – то о пластине.
В нашем случае, т. к. мы рассматриваем сосуды, работающие под действием внутреннего давления, то
1 – цилиндрическая оболочка;
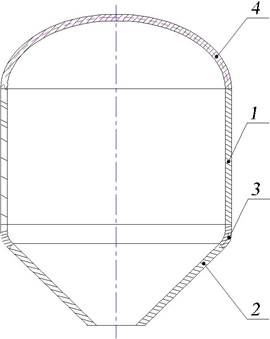
2 – коническое днище; 3 – торовый переход; 4 – эллиптическая крышка
Рисунок 1.1 – Схема корпуса аппарата изготовленного методом сварки
| б |
| Рисунок 1.2 – Оболочка вращения с обозначенными главными радиусами кривизны |
| а |
Расчёт и конструирование машин и аппаратов пищевых производств. Элементы теории и сборник задач Расчёт сосудов работающих под действием внутреннего избыточного давления
корпус сосуда представляет собой осесимметричную оболочку вращения.
Осесимметричная оболочка –это оболочка вращения,которая находится под действи-ем нагрузок, распределенных симметрично по отношению к ее оси.
Оболочка вращения –это такая оболочка,срединная поверхность которой образованавращением плоской кривой вокруг центральной оси, лежащей в плоскости этой кривой.
Основные характеристики осесимметричной оболочки вращения Условная срединная поверхность пластинки или оболочки–это поверхность,которая
находится на равных расстояниях от внутренней и наружной поверхности.
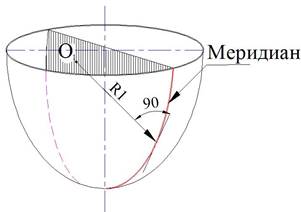
Меридиан – кривая линия,вращением которой образована срединная поверхность. Ра-диус кривизны меридиана в какой-либо точке срединной поверхности называется первым
главным радиусом кривизны R1 оболочки вэтой точке. Центр кривизны О1 лежит в этом случае в осевой плоскости, соответствующей данному меридиану (рисунок. 1.2, а).
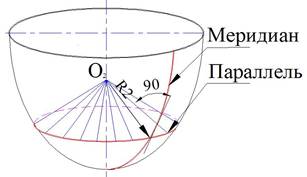
Параллель –кривая,образованная на сре-динной поверхности пересечением ее плоско-стью, перпендикулярной оси оболочки. Второй главный радиус кривизны R2 является обра-зующей конуса (рисунок. 1.2, б), вершина ко-торого О2 лежит на оси вращения, а боковая поверхность перпендикулярна к срединной по-верхности и пересекается с ней по параллели.
Соответственно, можно сделать вывод, что для цилиндра и конуса, у которых меридиана-ми являются прямые линии R 1, а для сфе-
ры R 1 R 2 R. Оболочки с одним веществен-ным главным радиусом (цилиндр, конус) назы-ваются оболочками одинарной кривизны или изогнутыми пластинками. Оболочки с двумя вещественными главными радиусами кривиз-ны в каждой точке (сфера, эллипсоид и тор) называются оболочками двоякой кривизны. Первые могут быть изготовлены с применени-ем недорогих технологических операций из листового материала с помощью гибки и свар-ки. Для изготовления вторых применяются бо-
лее дорогие операции: штамповка, обкатка и литье.