| 3б | Нормальная линейная однородная система 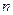 -го порядка с постоянными коэффициентами -го порядка с постоянными коэффициентами
|  Коэффициенты линейных комбинаций искомых функций постоянны.
Коэффициенты линейных комбинаций искомых функций постоянны.
 – матрица из коэффициентов при искомых функциях. – матрица из коэффициентов при искомых функциях.
| Уравнения записаны явно относительно первых производных; правые части уравнений представляют собой линейные комбинации искомых функций. | Матричный метод. Из характеристического уравнения  находят различные корни находят различные корни  и для каждого корня и для каждого корня 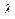 (с учетом его кратности) определяют соответствующее ему частное решение (с учетом его кратности) определяют соответствующее ему частное решение  . Общее решение имеет вид . Общее решение имеет вид  . Если б) . Если б) 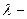 комплексный корень кратности 1 (один), тогда корнем характеристического уравнения является также сопряженное с комплексный корень кратности 1 (один), тогда корнем характеристического уравнения является также сопряженное с 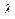 число число  . Вместо комплексных частных решений . Вместо комплексных частных решений  и и 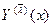 следует взять действительные частные решения следует взять действительные частные решения  и и 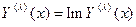 . .
|
| 3в | Нормальная линейная однородная система 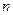 -го порядка с постоянными коэффициентами -го порядка с постоянными коэффициентами
| 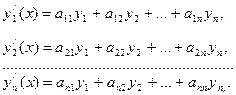 Коэффициенты линейных комбинаций искомых функций постоянны.
Коэффициенты линейных комбинаций искомых функций постоянны.
 – матрица из коэффициентов при искомых функциях. – матрица из коэффициентов при искомых функциях.
| Уравнения записаны явно относительно первых производных; правые части уравнений представляют собой линейные комбинации искомых функций. | Матричный метод. Если в)  корень кратности корень кратности 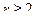 , то соответствующее этому корню решение системы ищут в виде вектора , то соответствующее этому корню решение системы ищут в виде вектора 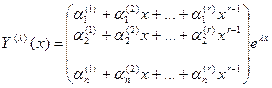 (**), коэффициенты которого (**), коэффициенты которого  определяются из системы линейных уравнений, получающихся приравниванием коэффициентов при одинаковых степенях определяются из системы линейных уравнений, получающихся приравниванием коэффициентов при одинаковых степенях  в результате подстановки вектора (**) в исходную систему. в результате подстановки вектора (**) в исходную систему.
|

абсолютно
 |  | ||||
| |||||
|

Рекомендации по применению достаточных признаков сходимости рядов
- Признак Даламбера применяют, если общий член ряда содержит показательные функции
 или факториалы
или факториалы  . Если же общий член ряда содержит только степенные функции
. Если же общий член ряда содержит только степенные функции  , где k − любое конечное вещественное число, признак Даламбера, как правило, ответа не даёт.
, где k − любое конечное вещественное число, признак Даламбера, как правило, ответа не даёт. 
- Интегральный признак Коши применяют, если легко найти первообразную общего члена ряда.
- Радикальный признак Коши применяют, если легко извлекается корень n -й степени из общего члена ряда. При этом,
 где k − любое конечное вещественное число. Также полезной бывает формула Стирлинга:
где k − любое конечное вещественное число. Также полезной бывает формула Стирлинга: 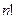 ~
~  при
при  .
. - Признаки сравнения применяют, когда легко подобрать для сравнения эталонные ряды, используя при этом сравнение бесконечно малых функций.
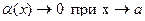
| |||
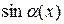 ~ ~ 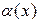
|  ~ ~ 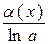
| ||
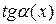 ~ ~ 
| 6а | 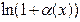 ~ ~ 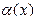
| |
 ~ ~ 
|  ~ ~ 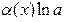
| ||
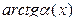 ~ ~ 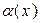
| 7а | 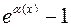 ~ ~ 
| |
 ~ ~ 
| 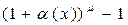 ~ ~ 
|
Следует иметь в виду, что при вычислении пределов отношений конечного числа б. б. складываемых функций слагаемые более низкого порядка роста можно отбрасывать, а сумму заменять слагаемым самого высокого порядка роста.
При  самый высокий порядок роста имеет показательная функция
самый высокий порядок роста имеет показательная функция  ; степенная функция
; степенная функция  имеет порядок роста, более низкий по сравнению с показательной функцией, но более высокий по сравнению с логарифмической; логарифмическая функция
имеет порядок роста, более низкий по сравнению с показательной функцией, но более высокий по сравнению с логарифмической; логарифмическая функция  имеет самый низкий порядок роста по сравнению и с показательной функцией, и со степенной. Это обозначают так:
имеет самый низкий порядок роста по сравнению и с показательной функцией, и со степенной. Это обозначают так:
 , при
, при  .
.
Очень эффективным при вычислении пределов оказывается применение следующих правил:
