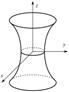
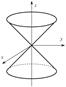
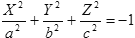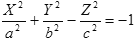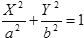Поверхности второго порядка
|  
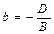 a³0 a³0
|
|
|  Уравнение прямой L
в отрезках
Уравнение прямой L
в отрезках
|  y= 0 Þ x=a
x= 0 Þ y=b y= 0 Þ x=a
x= 0 Þ y=b

|
|
| 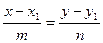 Уравнение прямой L
каноническое
Уравнение прямой L
каноническое
| 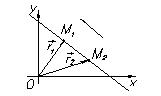 l =(m, n)
l =(m, n) çç L
M 1(x 1, y 1)Î L
" M (x, y)Î L
l =(m, n)
l =(m, n) çç L
M 1(x 1, y 1)Î L
" M (x, y)Î L
|
|
|  Уравнение прямой L,
проходящей через две данные точки M 1 и M 2
Уравнение прямой L,
проходящей через две данные точки M 1 и M 2
| 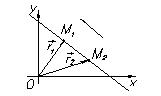 l =(m, n) çç L
M 1(x 1, , y 1)Î L
M 2(x 2, y 2)Î L
" M (x, y)Î L
m=x 2– x 1, n = y 2-– y 1
. l =(m, n) çç L
M 1(x 1, , y 1)Î L
M 2(x 2, y 2)Î L
" M (x, y)Î L
m=x 2– x 1, n = y 2-– y 1
.
|
|
| 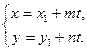 Уравнения прямой L
параметрические
Уравнения прямой L
параметрические
|
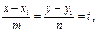 " t Î R 1 – параметр " t Î R 1 – параметр
|
| №
| Уравнения плоскости Р
| Рисунки, пояснения
|
|
| A ( x–x 1)+ B ( y–y 1)+ C ( z–z 1)=0
Уравнение плоскости P,
проходящей через данную точку М 1,,
перпендикулярно данному вектору N =(A, B, C)
| N = (A, B C)
 r = (x, y, z)
r 1 = (x 1, , y 1, z 1)
M 1(x 1, , y 1, z 1)Î P
" M (x, y, z) Î P
r = (x, y, z)
r 1 = (x 1, , y 1, z 1)
M 1(x 1, , y 1, z 1)Î P
" M (x, y, z) Î P
|
|
| Ax + By + Cz + D = 0
Общееуравнение плоскости P
| D = – Ax 1 – By 1 – Cz 1
|
|
| 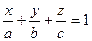 Уравнение плоскости P в отрезках
Уравнение плоскости P в отрезках
| y= 0, z= 0 Þ x=a
x= 0, z= 0 Þ y=b
x= 0, y= 0 Þ z=c
|
|
|  Уравнение плоскости P,
проходящей через три данные точки
Уравнение плоскости P,
проходящей через три данные точки
| M 1(x 1, y 1, z, 1)Î P, М 1 М Î Р
M 2(x 2, y 2, z 2)Î P, М 2 М 1Î Р
M 3(x 3, y 3, z 3)Î P, М 3 М 1Î Р
" M (x, y, z)Î P 
|
| Уравнения прямой L
в трехмерном пространстве (R 3)
| Рисунки, пояснения
|
|
|   ì A 1 x + B 1 y + C 1 z + D 1=0 î A 2 x + B 2 y + C 2 z + D 2=0.
Общееуравнение прямой L ì A 1 x + B 1 y + C 1 z + D 1=0 î A 2 x + B 2 y + C 2 z + D 2=0.
Общееуравнение прямой L
| 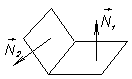  N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
l çç L, l =(m,n, p)=[ N 1, N 2] N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
l çç L, l =(m,n, p)=[ N 1, N 2]
|
|
|  Уравнения прямой L
канонические
Уравнения прямой L
канонические
| 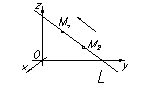 l çç L, l =(m, n, p)
M 1(x 1, y 1, z 1)Î L
"M(x, y, z)Î L l çç L, l =(m, n, p)
M 1(x 1, y 1, z 1)Î L
"M(x, y, z)Î L
|
|
|   Уравнение прямой L,
проходящей через две данные точки M 1 и M 2
Уравнение прямой L,
проходящей через две данные точки M 1 и M 2
| 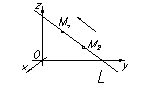 l çç L, l=(m, n, p), lt = M 1 M 2
m=x 2– x 1, n=y 2– y 1, p=z 2– z 1
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L l çç L, l=(m, n, p), lt = M 1 M 2
m=x 2– x 1, n=y 2– y 1, p=z 2– z 1
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L
|
|
|   Параметрические уравненияпрямой L
Параметрические уравненияпрямой L
|
 " t Î R 1
" t Î R 1
|
| Уравнения плоскости Р в R 3 в координатной форме
| Векторная форма уравнений
P, L в R 3 и R 2
| Уравнения прямой L в R 2 в координатной форме
|
| I R 3 Уравнения P и L, проходящих через данную точку М 1 R 2I
перпендикулярно данному вектору N
|
  N =(A, B, C)
r = (x, y, z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1, z 1)Î P
" M (x, y, z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0 N =(A, B, C)
r = (x, y, z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1, z 1)Î P
" M (x, y, z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0
| r-r 1 = M 1 M
M 1 M ^ N (P)
M 1 M ^ N (L)
(r-r 1, N) = 0
(M 1 M, N) = 0
Условие
ортогональности
векторов
| N = (A,B)
r = (x, y)
r 1 = (x 1, y 1)
M1 (x 1, y 1) Î L
" M (x, y) Î L
A (x-x 1)+ B (y-y 1) = 0
|
| II R 3 Общие уравнения R 2 II
|
|
Ax + By + Cz + D = 0
D = -Ax 1 - By 1 - Cz 1
|
(r,N) + D = 0
D = – (r1, N)
|
Ax + By +D = 0
D = -Ax 1 -By 1
|
| III R3 Через n фиксированных точек M R2 III
|
|
| n = 3
|
| n = 2
|
|
M 1(x 1 ,y 1, z, 1)Î P, М 1 М Î Р
M 2(x 2, y 2, z 2)Î P, М 2 М 1Î Р
M 3(x 3, y 3, z 3)Î P, М 3 М 1Î Р
" M (x,y,z)Î P  

|
M 1 Î P, L
M 2 Î P, L
" M Î P, L
M 3 Î P
| M 1(x 1 ,y 1) Î L,
M 2(x 2, y 2) Î L
" M (x, y) Î L
М 1 М çç М 2 М 1


|
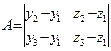
| (M 1 M, M 1 M 2, M 1 M 3)=0
Условие компланарности векторов
|
| [ M 1 M, M 1 M 2] = 0
Условие коллинеарности векторов
|
|
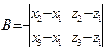

|
| A =y 2 -y 1; B = – (x 2 -x 1),
Û
A (x-x 1) + B (y-y 1) = 0
(1. I.)
|
| IV R 3 Уравнения в отрезках R 2 IV
|
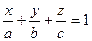 y= 0, z= 0 Þ x=a
x= 0, z= 0 Þ y=b
x= 0, y= 0 Þ z=c
y= 0, z= 0 Þ x=a
x= 0, z= 0 Þ y=b
x= 0, y= 0 Þ z=c
| r = xi+yj+zk
t = i/a +j/b +k/c
(r,t) = 1
t = (1 /a, 1 /b, 1 /c)
ç r ç cos (r,t) = 1/ ç t ç
|

 y= 0 Þ x=a
x= 0 Þ y=b y= 0 Þ x=a
x= 0 Þ y=b
|
| | | | | | | | | | | |
| Уравнения прямой L в R 3 в координатной форме
| Векторная форма уравнений прямой L в R 2 и R 3
| Уравнения прямой L в R 2 в координатной форме
|
| I Канонические уравнения прямой L I
|
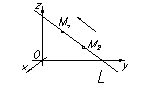 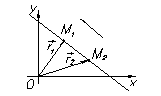 l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L
 
|
r-r 1= M 1 M çç l
r 2- r 1= M 1 M 2 çç l
[ r-r 1, l ]=0
[ M 1 M, l ]=0
| l =(m, n)
l =(m,n) çç L
M 1(x 1, y 1)Î L
M 2(x 2, y 2)Î L
" M (x, y)Î L

|
| II Параметрические уравнения прямой L II
|
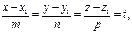 " t Î R 1 " t Î R 1
 

|
r-r 1 çç l, " t Î R 1
M 1 M çç l
r-r 1= M 1 M = tl
r=r 1+ tl
[ M 1 M, tl ]=0
|
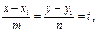 " t Î R 1 " t Î R 1
  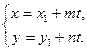
|
| III Уравнения прямой L, проходящей через две данные точки M 1 и M 2 III
|
l çç L, l=(m,n,p), lt = M 1 M 2
m=x 2– x 1, n=y 2– y 1, p=z 2– z 1
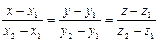
|
M 1 M çç M 1 M 2 çç l
M 1Î L, M 2Î L, " M Î L
[ M 1 M, M 1 M 2]=0
|
l çç L, l =(m,n), tl = M 1 M 2
m=x 2– x 1, n = y 2-– y 1
.


|
| IV Общие уравнения прямой L в R 3 (P 1Ç P 2)
| Уравнение прямой L с угловым коэффициентом k в R 2 V
|
 N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0. N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0.
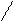 N 1 çç N 2 Û P 1Ç P 2 Û Rang N 1 çç N 2 Û P 1Ç P 2 Û Rang 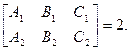
|
A x+ B y+ D =0, B ¹0
ß

 y = kx + b y = kx + b 
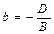 a³0 a³0
|
| | | | | | |
| Связь между уравнениями прямой L в R 3
| Связь между уравнениями прямой L в R 2
|
 Общие(2.IV) Общие(2.IV)

 Þ z0=0 Þ z0=0
 Þ M 0(x 0, y 0,0)Î L
или Þ M 0(x 0, y 0,0)Î L
или 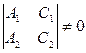 Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или  Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p) Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p)
 – канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß – канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß
 – через две
точки M 0Î L, M 1Î L (2.III) – через две
точки M 0Î L, M 1Î L (2.III)
 – общие(2.IV) – общие(2.IV)
| С угловым коэффициентом: (2.V)
y = kx+b  ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.
ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.

 через точки M 1Î L и M 2Î L
(1. III) (2.III) через точки M 1Î L и M 2Î L
(1. III) (2.III)
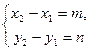 Þ Þ  – канонические(2.I)
ß
ì n (x-x 1)= m (y-y1)
í n (x-x 1)- m (y-y 1)=0,
î n = A; –m = B;
A (x-x 1)+ B (y-y 1)=0 M 1(x 1, y 1)Î L
N =(A, B)^ L (1.I)
ß
- Ax 1– B y1= D
Ax + By + D =0 – общее(1.II)
– канонические(2.I)
ß
ì n (x-x 1)= m (y-y1)
í n (x-x 1)- m (y-y 1)=0,
î n = A; –m = B;
A (x-x 1)+ B (y-y 1)=0 M 1(x 1, y 1)Î L
N =(A, B)^ L (1.I)
ß
- Ax 1– B y1= D
Ax + By + D =0 – общее(1.II)
|
| I Обозначения, принятые в таблице 2, {P1,P2} в R3
| I
| Обозначения, принятые в I таблице 2, {L1,L2} в R2
|
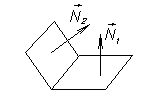 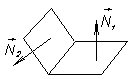  N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)
N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)
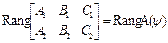

| R3 cos j =  N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2
N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2
N 1 =(A 1, B 1)
N 2 =(A 2, B 2)
| a)  N1=(A1,B1);N2=(A2,B2)
N1=(A1,B1);N2=(A2,B2)

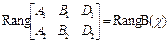 б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j =
б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j = 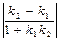 ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) =
ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) = 
|
| II Признаки взаимного расположения плоскостей {P1, P2} и прямых {L1, L2} II
|
| плоскости { Р 1, Р 2} в R n; n =3
| Как расположены P и L
| Прямые { L 1, L 2} в R n; n =2
|
P 1 Ç P 2 (пересекаются)
cos j= 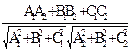 ¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y) ¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y)
|   N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
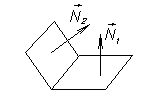 cos j ≠ ± 1 cos j ≠ ± 1
| L 1Ç L 2 (пересекаются)
a) 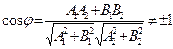 L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j=
L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j=  ¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c) ¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c)
|
P 1ïï P 2 (параллельны)
 cos j = ±1
cos j = ±1
|  N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
| L 1ïï L 2 (параллельны)
а) 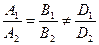 cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
|
P 1º P 2 (совпадают)
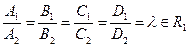 cosj = ±1
cosj = ±1
| 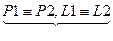 N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
| L 1º L 2 (совпадают)
а)  cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
|
| I P 1 || P 2, L 1 || L 2 в R 3
координатная форма
| P 1 || P 2, L 1 || L 2,  векторная форма
векторная форма
| L 1 || L 2 в R 2II
координатная форма
|
 Ü
Ü

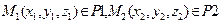
| 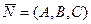 
  
| 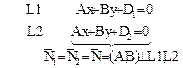 Þ
Þ
 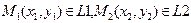
|
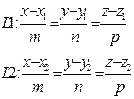 
|
| 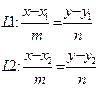 
|
 Ü Ü
|  h – высота треугольника h – высота треугольника
| Þ 
|
| III Прямые L 1 и L 2 скрещиваются в R 3
P 1 || P 2 (L 1Ì P 1, L 2Ì P 2)
| Прямая L и плоскость P пересекаются в R 3 IV
{ P Ç L }= M 1
|


 (d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота (d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота
| 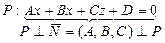
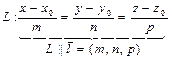 M 0(x 0, y 0, z 0) Î L
M 0(x 0, y 0, z 0) Î L
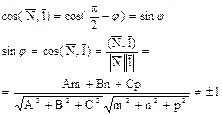 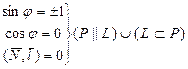 sin j = 0 Û L ^ P, l ïï N
sin j = 0 Û L ^ P, l ïï N
|
| | | | |
|
| к = n – r, Rang A = r
|
| |
|
| AX = B

| 
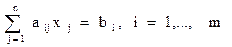
|
| |
| Система m линейных уравнений с n неизвестными
| |
| r = 1
гиперплоскость
к = n –1
| к = 1
прямая в R r+1
n – r = 1
| к-мерная плоскость Р к0 в R n, проходящая через начало координат В =0 (СОЛУ) – система
однородных линейных уравнений
| Общее решение произвольной системы линейных уравнений В ¹0 (ОРСЛУ)
| |
| матричная форма
| координатная форма
|
| матричная форма
| координатная форма
|
|
| |

|

|

| 
|
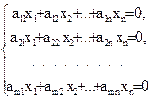
|

| |
| | Плоскость в R3
n =3
|
|
|
|
|

|  Уравнение плоскости в отрезках;
Уравнение плоскости в отрезках;
|  Rang A = r = n –1
n = r + 1
AX=B
Rang A = r = n –1
n = r + 1
AX=B
| AX =0
rang A=r,
x1,x2,..,xr – базисные неизвестные. Число базисных неизвестных равно r.
| xr+1, xr+2,..,xn – свободные неизвестные
Число свободных неизвестных равно k=n – r
| Отбросить строки, не вошедшие в базисный минор, перенести свободные неизвестные в правые части уравнений, а дальше следует применить метод Гаусса, Крамера или матричный.
| |
| | | | | | | | | | | | | | | |


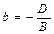 a³0
a³0
 Уравнение прямой L
в отрезках
Уравнение прямой L
в отрезках
 y= 0 Þ x=a
x= 0 Þ y=b
y= 0 Þ x=a
x= 0 Þ y=b

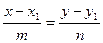 Уравнение прямой L
каноническое
Уравнение прямой L
каноническое
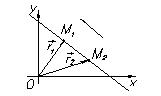 l =(m, n)
l =(m, n) çç L
M 1(x 1, y 1)Î L
" M (x, y)Î L
l =(m, n)
l =(m, n) çç L
M 1(x 1, y 1)Î L
" M (x, y)Î L
 Уравнение прямой L,
проходящей через две данные точки M 1 и M 2
Уравнение прямой L,
проходящей через две данные точки M 1 и M 2
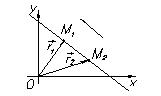 l =(m, n) çç L
M 1(x 1, , y 1)Î L
M 2(x 2, y 2)Î L
" M (x, y)Î L
m=x 2– x 1, n = y 2-– y 1
.
l =(m, n) çç L
M 1(x 1, , y 1)Î L
M 2(x 2, y 2)Î L
" M (x, y)Î L
m=x 2– x 1, n = y 2-– y 1
.
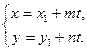 Уравнения прямой L
параметрические
Уравнения прямой L
параметрические
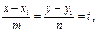 " t Î R 1 – параметр
" t Î R 1 – параметр
 r = (x, y, z)
r 1 = (x 1, , y 1, z 1)
M 1(x 1, , y 1, z 1)Î P
" M (x, y, z) Î P
r = (x, y, z)
r 1 = (x 1, , y 1, z 1)
M 1(x 1, , y 1, z 1)Î P
" M (x, y, z) Î P
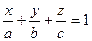 Уравнение плоскости P в отрезках
Уравнение плоскости P в отрезках
 Уравнение плоскости P,
проходящей через три данные точки
Уравнение плоскости P,
проходящей через три данные точки


 ì A 1 x + B 1 y + C 1 z + D 1=0 î A 2 x + B 2 y + C 2 z + D 2=0.
Общееуравнение прямой L
ì A 1 x + B 1 y + C 1 z + D 1=0 î A 2 x + B 2 y + C 2 z + D 2=0.
Общееуравнение прямой L

 N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
l çç L, l =(m,n, p)=[ N 1, N 2]
N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
l çç L, l =(m,n, p)=[ N 1, N 2]
 Уравнения прямой L
канонические
Уравнения прямой L
канонические
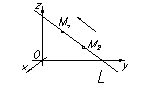 l çç L, l =(m, n, p)
M 1(x 1, y 1, z 1)Î L
"M(x, y, z)Î L
l çç L, l =(m, n, p)
M 1(x 1, y 1, z 1)Î L
"M(x, y, z)Î L

 Уравнение прямой L,
проходящей через две данные точки M 1 и M 2
Уравнение прямой L,
проходящей через две данные точки M 1 и M 2

 Параметрические уравненияпрямой L
Параметрические уравненияпрямой L
 " t Î R 1
" t Î R 1

 N =(A, B, C)
r = (x, y, z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1, z 1)Î P
" M (x, y, z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0
N =(A, B, C)
r = (x, y, z)
r 1 = (x 1, y 1, z 1)
M 1(x 1, y 1, z 1)Î P
" M (x, y, z) Î P
A(x-x 1)+ B (y-y 1)+ C (z-z 1)=0



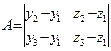
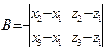


 y= 0 Þ x=a
x= 0 Þ y=b
y= 0 Þ x=a
x= 0 Þ y=b
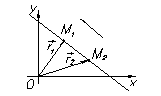 l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L
l =(m,n,p)
l=(m,n,p)ïï L
M 1(x 1, y 1, z 1)Î L
M 2(x 2, y 2, z 2)Î L
"M(x, y, z)Î L


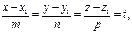 " t Î R 1
" t Î R 1


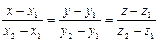



 N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0.
N 1=(A 1, B 1, C 1)
N 2=(A 2, B 2, C 2) N 1çç N 2
L ={ P 1Ç P 2}
.
ì A 1 x + B 1 y + C 1 z + D 1=0,
î A 2 x + B 2 y + C 2 z + D 2=0.

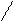 N 1 çç N 2 Û P 1Ç P 2 Û Rang
N 1 çç N 2 Û P 1Ç P 2 Û Rang 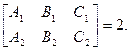

 y = kx + b
y = kx + b 
 Общие(2.IV)
Общие(2.IV)

 Þ z0=0
Þ z0=0
 Þ M 0(x 0, y 0,0)Î L
или
Þ M 0(x 0, y 0,0)Î L
или 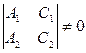 Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или
Þ y1=0 Þ M 1(x 1,0, z 1)Î L
или  Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p)
Þ x 2=0 Þ M 2(0, y 2,z2)Î L
N 1=(A 1, B 1, C 1),ü
N 2=(A 2, B 2 ,C 2) þ Û l =[ N 1, N 2]=(m,n,p)
 – канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß
– канонические (2.I)
-
ì x-x 0+ mt,
í y-y 0+ nt, – параметрические(2.II)
î z =0+ pt
ß
 – через две
точки M 0Î L, M 1Î L (2.III)
– через две
точки M 0Î L, M 1Î L (2.III)
 – общие(2.IV)
– общие(2.IV)
 ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.
ß
ì x = x 1, y=kx 1+ b = y 1 Þ M 1(x 1, y 1)Î L,
î x = x 2, y=kx 2+ b = y 2 Þ M 2(x 2, y 2)Î L.

 через точки M 1Î L и M 2Î L
(1. III) (2.III)
через точки M 1Î L и M 2Î L
(1. III) (2.III)
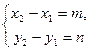 Þ
Þ 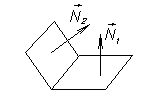

 N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)
N 1=(A 1, B 1, C 1);
N 2=(A 2, B 2,C2)
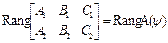

 N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2
N 1=(A 1, B 1, C 1); N 2=(A 2, B 2, C 2)
R2

 N1=(A1,B1);N2=(A2,B2)
N1=(A1,B1);N2=(A2,B2)

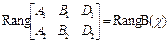 б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j =
б) L 1: y=k 1x+ b 1
L 2: y=k 2x+ b 2
tg j = 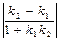 ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) =
ß
k 1= tg a1; k 2= tg a2
tg j =tg (a2 – a1) = 
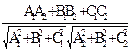 ¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y)
¹±1
P 1^ P 2 Û N1^N2 Û cos j=0
{ P 1Ç P 2}= L, L Î P 1, L Î P 2
Rang A (y)=
= Rang B (y)= 2 < 3= n
совместная неопределенная система (y)

 N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
N1ïï N2
j ¹ p k,
k =0, ±1, ±2,...
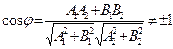 L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j=
L 1^ L 2Û N 1^ N 2 Û cos j = 0
б) tg j=  ¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c)
¹0
1+ k 1 k 2 ¹ 0
L 1^ L 2 Û1+ k 1 k 2 =0 Û
Û k 2= -1/ k 1
{ L 1Ç L 2}= M, M Î L 1, M Î L 2
Rang A (c)=
= Rang B (c)= 2= n
совместная определенная система (c)
 cos j = ±1
cos j = ±1
 N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
N 1 =lN 2; D 1¹ lD 2
l Î R 1
1= Rang A (y,c) <
< Rang B (y,c) = 2
системы (y),(c) несовместны
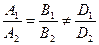 cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
cos j = ±1
б) k 1 = k 2; b 1 ¹ b 2
tg j = 0
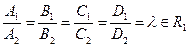 cosj = ±1
cosj = ±1
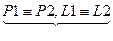 N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
N 1= lN 2; D 1 = lD 2; l Î R 1
Rang A (y,c)=
= Rang B (y,c)= 1
совместные неопределенные системы (y), (c)
 cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
cosj = ±1
б) k 1 = k 2, b 1 = b 2
tgj = 0
 векторная форма
векторная форма
 Ü
Ü

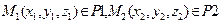
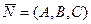




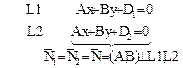 Þ
Þ

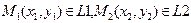
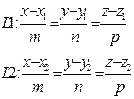

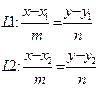

 Ü
Ü
 h – высота треугольника
h – высота треугольника



 (d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота
(d(L 1, L 2)=0Û L 1Ç L 2);П(М 1 М 2, l 1 ,l 2) –параллелепипед, построенный на векторах М 1 М 2, l 1 ,l 2,, h – его высота
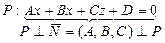
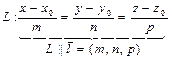 M 0(x 0, y 0, z 0) Î L
M 0(x 0, y 0, z 0) Î L
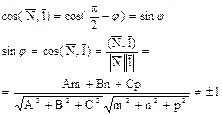
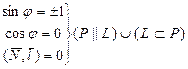 sin j = 0 Û L ^ P, l ïï N
sin j = 0 Û L ^ P, l ïï N
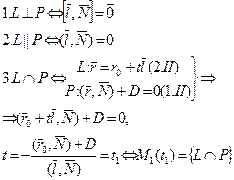
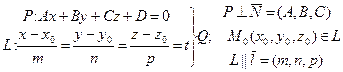
 (2.II) Þ
(2.II) Þ 



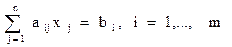




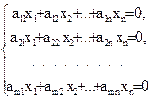


 Уравнение плоскости в отрезках;
Уравнение плоскости в отрезках;
 Rang A = r = n –1
n = r + 1
AX=B
Rang A = r = n –1
n = r + 1
AX=B

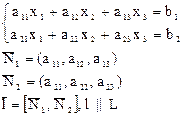
 АХ 1 = 0 АХ 2 = 0 АХ к = 0, k=n–r.
АХ 1 = 0 АХ 2 = 0 АХ к = 0, k=n–r.
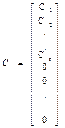 АС=В
АС=В
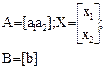 АХ=В
АХ=В
 Уравнение прямых в отрезках
Уравнение прямых в отрезках


 AX=A (X0+C)=
= AX 0+ AC= O+ B=B
AX=A (X0+C)=
= AX 0+ AC= O+ B=B
 Прямая в Rn=Rr + 1 n = r+ 1, k = 1
Прямая в Rn=Rr + 1 n = r+ 1, k = 1
 параметрические уравнения,
a 1 – параметр, свободная неизвестная
параметрические уравнения,
a 1 – параметр, свободная неизвестная
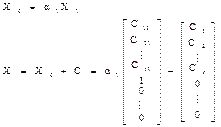
 – канонические уравнения
– канонические уравнения