| № п/п | Цель исследования | Действия | Вывод |
| Найти область определения функции | Найти точки, в которых функция не определена или не задана (точки разрыва графика функции) | Исключить найденные точки из области определения функции | |
| Найти вертикальные асимптоты | Вычислить односторонние пределы функции в точках разрыва и в точках, «подозрительных» на разрыв для кусочно-аналитической функции | Если хотя бы один из односторонних пределов в исследуемой точке равен бесконечности, то график функции имеет вертикальную асимптоту:
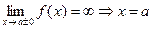 – вертикальная асимптота – вертикальная асимптота
| |
| Исследовать функцию на четность и нечетность | Если  ,
то функция четная.
Если ,
то функция четная.
Если  ,
то функция нечетная ,
то функция нечетная
| Ограничиться исследованием функции на интервале  . График четной функции симметричен относительно оси OY, график нечетной функции симметричен относительно начала координат . График четной функции симметричен относительно оси OY, график нечетной функции симметричен относительно начала координат
| |
| Исследовать функцию на периодичность | T – период функции – (наименьшее из всех возможных значений, удовлетворяющих уравнению:
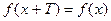
| Ограничиться исследованием на интервале, по длине равном периоду T, за пределы интервала продолжить график функции периодическим образом | |
| Найти точки пересечения с осями координат | Решив уравнение  , найти , найти 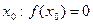 .
Найти .
Найти 
| Точка пересечения графика с осью OX:  .
Точка пересечения графика с осью OY: .
Точка пересечения графика с осью OY: 
| |
| Найти наклонные, в частности, горизонтальные асимптоты | Вычислить пределы  и и 
| Если k и b – конечные числа, то уравнение наклонных асимптот  , причем, при , причем, при  асимптота горизонтальная асимптота горизонтальная 
|
Исследования функции с применением производных
| № п/п | Цель исследования | Действия и вывод | ||||
| Найти интервалы монотонности и точки локальных экстремумов функции | 1.1.1. Найти критические точки первого порядка 
 или или  , или , или  не существует
(необходимоеусловие существования экстремума функции в точке);
1.2.1. Применить первое достаточное условие существования экстремума функции в критической точке: не существует
(необходимоеусловие существования экстремума функции в точке);
1.2.1. Применить первое достаточное условие существования экстремума функции в критической точке:
| |||||

| 
| 
| 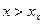
| |||

| ¾ | Критическая точка первого порядка | + | |||
| y | Функция убывает |  точка минимума точка минимума
| Функция возрастает | |||

| 
| 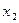
| 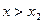
| |||

| + | Критическая точка первого порядка | ¾ | |||

| Функция возрастает |  точка максимума точка максимума
| Функция убывает | |||
1.2.2. Если 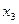 и и 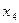 – стационарные точки (все производные до (2к –1) порядка равны нулю), можно применить второе достаточное условие существования экстремума функции в точке: – стационарные точки (все производные до (2к –1) порядка равны нулю), можно применить второе достаточное условие существования экстремума функции в точке:
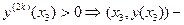 точка локального минимума; точка локального минимума;
 точка локального максимума; точка локального максимума;
 – в точке – в точке  экстремума нет. экстремума нет.
| ||||||
| Найти интервалы выпуклости и вогнутости графика функции и точки перегиба | 2.1. Найти критические точки второго порядка 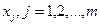 : :
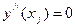 или или  , или , или  не существует
(необходимое условие существования точки перегиба графика);
2.2. Применить достаточныеусловия выпуклости и вогнутости графика и существования точек перегиба: не существует
(необходимое условие существования точки перегиба графика);
2.2. Применить достаточныеусловия выпуклости и вогнутости графика и существования точек перегиба:
| |||||

| 
| 
| 
| |||

| + | Критическая точка второго порядка, точка непрерывности | ¾ | |||
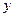
| График функции вогнутый |  точка перегиба точка перегиба
| График функции выпуклый | |||
Неопределенный интеграл
Метод непосредственного интегрирования
 |











