Министерство общего и профессионального образования РФ
-------------------------------------------------------------------------------------------------------
Новгородский Государственный Университет
Им. Ярослава Мудрого
Кафедра ФТТиМ
Контроль параметров АЦП
Реферат по дисциплине:
Испытания изделий электронной техники.
Выполнил:
Студент группы 4031
_______Галинко В.Ю.
«___»_____________1999
Проверил:
Преподаватель каф. ФТТиМ
_______Крутяков.Л.Н.
«___»_____________1999
Новгород
Содержание
| Введение | |
| 1. Основные структуры ИМС АЦП | |
| 2. Характеристики ИМС АЦП | |
| 3. Контроль статических параметров ИМС АЦП | |
| 4. Контроль динамических параметров ИМС АЦП | |
| Список использованных источников | |
Введение
Цифро-аналоговые и аналого-цифровые преобразователи АЦП находят.широкое применение в различных областях современной науки и техники. Они являются неотъемлемой составной частью цифровых измерительных приборов, систем преобразования и отображения информации, программируемых источников питания, индикаторов на электронно-лучевых трубках, радиолокационных систем, установок для контроля элементов и микросхем, а также важными компонентами различных автоматических систем контроля и управления, устройств ввода—вывода информации ЭВМ. На их основе строят преобразователи и генераторы практически любых функций, цифроуправляемые аналоговые регистрирующие устройства, корреляторы, анализаторы спектра и т. д. Велики перспективы использования быстродействующих преобразователей в телеметрии и телевидении. Несомненно, серийный выпуск малогабаритных и относительно дешевых АЦП еще более усилит тенденцию проникновения метода дискретно-непрерывного преобразования в сферу науки и техники. Одним из стимулов развития цифро-аналоговых и аналого-цифровых преобразователей в интегральном исполнении в последнее время является широкое распространение микропроцессоров и методов цифровой обработки данных. В свою очередь потребность в АЦП стимулирует их разработку и производство с новыми, более совершенными характеристиками. В настоящее время применяют три вида технологии производства АЦП: модульную, гибридную и полупроводниковую. При этом доля производства полупроводниковых интегральных схем (ИМС ЦАП и ИМС АЦП) в общем объеме их выпуска непрерывно возрастает и в недалеком будущем, по-видимому, в модульном и гибридном исполнениях будут выпускаться лишь сверхточные и сверхбыстродействующие преобразователи с достаточно большой рассеиваемой мощностью.
В данной главе рассматриваются основные структуры, характеристики и методы контроля интегральных микросхем АЦП.
Основные структуры ИМС АЦП
|
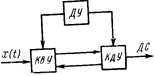
| Рис. 1. Обобщенная структурная схема АЦП |
Обобщенная структурная схема АЦП (рис.1) представляет собой дискретизирующее устройство ДУ, тактирующее работу квантующего КвУ и кодирующего КдУ устройств. На вход квантующего устройства поступает преобразуемый сигнал x(t), а с выхода кодирующего устройства снимается дискретный сигнал ДС, который для АЦП в интегральном исполнении обыччно имеет форму двоичного параллельного кода. В результате равномерного квантования мгновенное значение x i непрерывной величины x(t) представляется в виде конечного числа п ступеней квантования Δх:
Xi=nΔx=x ±Δk,
где Δk - погрешность квантования, обусловленная тем, что преобразуемая величина х может содержать нецелое число п ступеней квантования Δх.
Максимально возможная погрешность квантования (погрешность дискретности) определяется ступенью квантования, т. е.
Δkmax= Δx
Для известного диапазона xmax максимально возможное число дискретных значений преобразуемого сигнала х (включая х==0)
nmax=(xmax/ Δx+1)
При этом, как правило, погрешность квантования не должна превышать общую погрешность преобразования.
Следовательно, если известно значение допустимой относительной погрешности преобразования γmaх, то при определении ступени квантования необходимо учитывать соотношение
Δx ≤ (γmaх /100)*xmax
Кроме того, следует учитывать, что АЦП обладают определенным порогом чувствительности Хп.ч, т. е. способностью вызывать изменение выходной информации преобразователя при воздействии на его вход наименьшего значения преобразуемого сигнала. Поэтому значениеΔx должно превышать Хп.ч и удовлетворять неравенству
Хп.ч < Δx ≤ (γmaх /100)*xmax
Реализацию обобщенной структуры можно осуществить различными способами, которые рассмотрены ниже. Независимо от способа построения АЦП всем им присуща методическая погрешность, обусловленная погрешностью квантования Δx.
В зависимости от области применения АЦП их основные характеристики (точность, разрешающая способность, быстродействие) могут существенно отличаться. При использовании АЦП в измерительных устройствах главную роль играет точность преобразования, а быстродействие этих устройств ограничено реальной скоростью регистрации результата измерения. При использовании АЦП в качестве устройства ввода измерительной информации в ЭВМ от него требуется быстродействие в большей степени.
Широкое применение АЦП в различных областях науки и техники явилось предпосылкой создания разных структур АЦП, каждая из которых позволяет решить определенные задачи, предъявляемые к АЦП в каждом конкретном случае. Из всего многообразия существующих методов аналого-цифрового преобразования в интегральной технологии нашли применение в основном три:
1) метод прямого (параллельного) преобразования;
2) метод последовательного приближения (поразрядного уравновешивания);
3) метод интегрирования.
Каждый из этих методов позволяет добиться наилучших параметров (быстродействия, разрешающей способности, помехоустойчивости и т. д.). Потребность в АЦП с оптимальными параметрами или с отдельными экстремальными параметрами обусловила появление структур преобразователей, использующих комбинацию перечисленных методов. Рассмотрим структурные схемы АЦП, нашедших наибольшее распространение в интегральной технологии.
В АЦП с параллельным преобразованием входной сигнал прикладывается одновременно ко входам всех компараторов. В каждом компараторе он сравнивается с опорным сигналом, значение которого эквивалентно определенной кодовой комбинации. Опорный сигнал снимается с узлов резистивного делителя, питаемого от источника опорного напряжения. Число возможных кодовых комбинаций (а следовательно, число компараторов) равно 2m— 1, где т— число разрядов АЦП. АЦП прямого преобразования обладают самым высоким быстродействием среди других типов АЦП, определяемым быстродействием компараторов и задержками в логическом дешифраторе. Недостатком их является необходимость в большом количестве компараторов. Так, для 8-разрядного АЦП требуется 255 компараторов. Это затрудняет реализацию многоразрядных (свыше 6—8-го разрядов) АЦП в интегральном исполнении. Кроме того, точность преобразования ограничивается точностью и стабильностью каждого компаратора и резистивного делителя. Тем не менее на основе данного принципа строят наиболее быстродействующие АЦП со временем преобразования в пределах десятков и даже единиц наносекунд, но ограниченной разрядности (не более шести разрядов).
АЦП последовательного приближения имеет несколько меньшее быстродействие, но существенно большую разрядность (разрешающую способность). В нем используется только один компаратор, максимальное число срабатываний которого за один цикл измерения не превышает числа разрядов преобразователя. Суть такого метода преобразования заключается в последовательном сравнении входного преобразуемого напряжения Us с выходным напряжением образцового ЦАП, изменяющимся по закону последовательного приближения до момента наступления их равенства (с погрешностью дискретности). Входной сигнал Ux с помощью аналогового компаратора КН сравнивается с выходным сигналом образцового ЦАП, который управляется в свою очередь регистром последовательного приближения РгПП. При запуске схемы РгПП устанавливается генератором Г в исходное состояние. При этом на выходе ЦАП формируется напряжение, соответствующее половине диапазона преобразования, что обеспечивается включением его старшего разряда 100... 0. Если Us меньше выходного напряжения ЦАП, то старший разряд выключается, включается второй по старшинству разряд (на входе ЦАП код 0100...0), что соответствует 'формированию на выходе ЦАП напряжения, равного половине предыдущего. В случае если Их превышает это напряжение, то дополнительно включается третий разряд (на входе ЦАП код 0110...0), что приводит к увеличению выходного напряжения ЦАП в 1,5 раза. При этом выходное напряжение ЦАП вновь сравнивается с напряжением Ux и т. д. Описанная процедура повторяется т раз (где m — число разрядов АЦП). В итоге на выходе ЦАП формируется напряжение, отличающееся от входного преобразуемого напряжения Ux не более чем на единицу младшего разряда ЦАП. Результат преобразования напряжения Ux в его цифровой эквивалент—параллельный двоичный код Nx— снимается с выхода РгПП. Очевидно, погрешность преобразования и быстродействие такого устройства определяются в основном параметрами ЦАП (разрешающей способностью, линейностью, быстродействием) и компаратора (порогом чувствительности, быстродействием). Преимуществом рассмотренной схемы является возможность построения многоразрядных (до 12 разрядов и выше) преобразователей сравнительно высокого быстродействия (время 'преобразования 'порядка нескольких сот наносекунд). На основе метода последовательного приближения реализована и серийно выпускается ИМС 12-разрядного АЦП К572ПВ1 с временем преобразования 100 мкс.
Наиболее простыми по структуре среди интегрирующих преобразователей являются АЦП с преобразованием напряжения в частоту, построенные на базе интегрирующего усилителя и аналогового компаратора. Погрешность их преобразования определяется нестабильностью порога срабатывания компаратора и постоянной времени интегратора. Более высокими метрологическими характеристиками обладают АЦП, реализованные по принципу двойного интегрирования (например, ИМС, 11-разрядного АЦП К572ПВ2), поскольку при этом практически удается исключить влияние на погрешность преобразования нестабильности порога срабатывания компаратора и постоянной времени интегратора.
Анализ описанных методов преобразования и структурных схем АЦП позволяет сделать вывод, что наибольшим быстродействием обладают АЦП прямого преобразования, однако их разрядность невысока. АЦП поразрядного уравновешивания, обладая средним быстродействием, дают возможность получить достаточно высокую разрешающую способность. Но помехозащищенность тех и других преобразователей невысока. АЦП интегрирующего типа, обладая наименьшим быстродействием, обеспечивают наибольшую помехозащищенность и точность преобразования.
Характеристики ИМС АЦП
Основными параметрами, характеризующими ИМС АЦП, являются разрешающая способность, нелинейность, коэффициент преобразования, погрешность полной шкалы, смещение нуля, абсолютная погрешность, дифференциальная нелинейность, монотонность, время преобразования.
Разрешающая способность определяется числом дискретных значений выходного сигнала преобразователя, составляющих его предел преобразования. Чем больше число дискретных значений, тем выше разрешающая способность преобразователя. Двоичный m-разрядный преобразователь имеет 2m дискретных значений, а его разрешающая способность равна 1/2m. В преобразователях различают наименьший и наибольший значащие разряды. В двоичной системе кодирования наименьший значащий разряд — это разряд, имеющий наименьший вес. Вес младшего разряда определяет разрешающую способность. Наибольший значащий разряд соответствует наибольшему весу. В двоичной системе кодирования наибольший значащий разряд имеет вес 1/2 номинального значения максимально возможного выходного сигнала при всех включенных разрядах (полной шкалы преобразования).

Разрешающая способность характеризует как ЦАП, так и АЦП и может выражаться либо в процентах, либо в долях полной шкалы. Например, 12-разрядный АЦП имеет разрешающую способность 1/4096, или 0,0245% от значения полной шкалы. Преобразователь с полной шкалой напряжения 10 В может обеспечивать изменение выходного кода на единицу при изменении входного напряжения на 2,45 мВ. Аналогично 12-разрядный ЦАП дает изменение выходного напряжения на 0,0245% от значения полной 'шкалы при изменении двоичного входного кода на один двоичный разряд. Разрешающая способность является скорее расчетным параметром, а не технической характеристикой, поскольку она не определяет ни точность, ни линейность преобразователя.
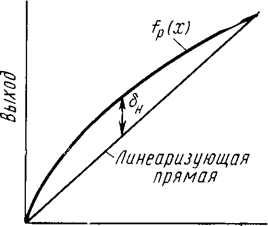
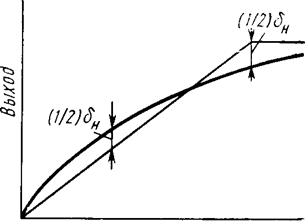
Нелинейность dн, или интегральная нелинейность, характеризуется отклонением dн (х) реальной характеристики преобразователя fp(x) от прямой. При этом значение dн (х) зависит от метода линеаризации. Рис. 2, а иллюстрирует способ линеаризации, когда линеаризующая прямая проходит через крайние точки реальной характеристики ЦАП. При этом наблюдается максимальная погрешность линейности (нелинейность dн). На рис. 2,б прямая проводится таким образом, что максимальное отклонение fp(x) от прямой получается в два раза меньше. Однако для этого необходимо знать характер реальной характеристики ЦАП, что очень 'сложно обеспечить в серийном производстве. Поэтому, как правило, погрешность линейности определяют при прохождении линеаризующей прямой через крайние точки характеристики fp (х). Для определения нелинейности (которая обычно выражается в процентах от полной шкалы или в долях единицы младшего разряда) необходимо знать аналитическую зависимость между выходным аналоговым сигналом ЦАП и его цифровым входом. Для ЦАП с двоичными т-разрядами аналоговый выход Uвых зависит от входного двоичного кода в идеальном случае (в отсутствие погрешностей преобразования) таким образом:
Uвых = Uоп(B12-1+B22-2+…+ Bm2-m), (1)
где B1, B2,..., Bm—коэффициенты двоичного числа, имеющие значение единицы или нуля (что соответствует включению или выключению разряда); Uon— опорное напряжение ЦАП. Так как
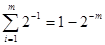
то выходное напряжение ЦАП при всех включенных разрядах ( B1, B2,..., Bm = 1) определяется соотношением
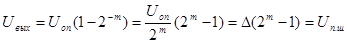 (2)
(2)
Таким образом, при включении всех разрядов выходное напряжение ЦАП, равное напряжению полной шкалы Uп.ш, отличается от опорного напряжения Uоп на значение младшего разряда преобразователя Δ:
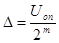 (3)
(3)
При включении i-ro разряда выходное напряжение ЦАП
Uвых=Uоп2-i (4)
Выражение (1) показывает линейную зависимость между аналоговым выходом и цифровым входом преобразователя. Следовательно, сумма аналоговых выходных величин, полученная для любой комбинации разрядов, действующих независимо, должна быть равна аналоговому сигналу, который получается при одновременном включении всех разрядов этой комбинации.
 |
Это является основой простого и эффективного контроля нелинейности: включаются различные комбинации разрядов и регистрируется соответствующий аналоговый сигнал. Затем каждый разряд этой комбинации включается отдельно и записывается соответствующее ему значение выходного напряжения. Алгебраическая сумма этих значений сравнивается с суммой, получаемой для всех разрядов выбранной комбинации, включённых одновременно. Разность сумм и будет погрешностью линейности для данной точки выходной характеристики преобразователя. Наихудшим случаем для погрешности линейности является включение всех разрядов, поскольку при этом погрешность определяется суммой погрешностей всех разрядов.
|
Преобразователь считается линейным, если его максимальная погрешность линейности δn не превышает 1/2 значения младшего разряда Δ. Оценку линейности АЦП проводят так же, как и для ЦАП.
Таким образом, нелинейность характеризует как ЦАП, так и АЦП и наряду с дифференциальной нелинейностью имеет первостепенное значение для оценки качества преобразователей, поскольку все другие погрешности (смещение нуля, погрешность полной шкалы и т. д.) могут быть сведены к нулю соответствующими регулировками.
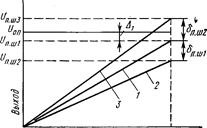
Коэффициент преобразования Кпр определяет наклон характеристики преобразователя. Как отмечалось, для идеального ЦАП наклон характеристики должен быть таким, чтобы при включении всех разрядов (двоичный код полной шкалы No на его цифровых входах равен 111...1) выходное напряжение полной шкалы Uп.ш ЦАП было меньше опорного напряжения Uоп на значение младшего разряда Δ, что соответствует прямой 1 на рис. 3 [соотношение (2)]. Для ЦАП с токовым выходом наклон характеристики определяется номиналом резистора обратной связи Roc (Рис. 4), который находится в составе преобразователя и предназначен для включения в цепь обратной связи усилителя-преобразователя тока в напряжение. При номинальном значении R ос напряжение Un.ш отличается от Uon на значение младшего разряда Δ. Если номинал Roc больше, то коэффициент преобразования возрастает (прямая 3 на рис. 3), если меньше,—то уменьшается (прямая 2 на рис 3). Это объясняется тем, что абсолютные значения младшего разряда Δ2 и Δ3 для характеристик 2 и 3 рис. 3 отличаются от расчетного номинального значения Δ1, определяемого соотношением (3). При этом фактические значения младших разрядов преобразования определяются соотношением
Δф=Uп.ш.ф./(2m-1)
где Uп.ш.ф.—фактическое значение полной шкалы преобразователя.
Погрешность полной шкалы δп.ш отражает степень отклонения реального коэффициента преобразования от расчетного, т. е. под δп.ш понимают разность между номинальным значением полной шкалы преобразователя Uп.ш.н, определяемым соотношением (2), и его фактическим значением Uп.ш.ф. Таким образом, для ЦАП
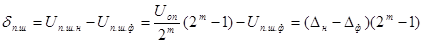
де Δн и Δф — номинальное и фактическое значения единицы младшего разряда преобразователя.
Относительная погрешность полной шкалы определяется выражением
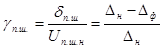
и, следовательно, не зависит от коэффициента преобразования ЦАП.
Погрешность полной шкалы АЦП характеризуется отклонением действительного входного напряжения от его расчетного значения для полной шкалы выходного кода. Она может быть обусловлена погрешностями опорного напряжения Uoп, многозвенного резистивного делителя, коэффициента усиления усилителя и т. д. Погрешность шкалы может быть скорректирована с помощью регулирования коэффициента усиления выходного усилителя или опорного напряжения.
Смещение нуля (погрешность нуля) равно выходному напряжению ЦАП при нулевом входном коде или среднему значению входного напряжения АЦП, необходимому для получения нулевого кода на его выходе. Смещение нуля вызвано током утечки через разрядные ключи ЦАП,
напряжением смещения выходного усилителя либо компаратора. Данную погрешность можно скомпенсировать с помощью внешней по отношению к ЦАП или АЦП регулировки нулевого смещения. Погрешность нуля δ0 может быть выражена в процентах от полной шкалы или в долях младшего разряда. Следует отметить, что погрешность полной шкалы определяют с учетом смещения нуля характеристики преобразователя, в то время как при определении погрешности линейности линеаризующая прямая должна проходить через начало реальной функции преобразования fр(х), т. е. смещение нуля δ0 необходимо корректировать, чтобы не внести погрешность в измерение линейности, поскольку она суммируется всякий раз при считывании выходного сигнала. Действительно, для ЦАП справедливо неравенство
Uвых(B1+B2+…+Bm)+δ0≠UвыхB1+ UвыхB2+…+ UвыхBm+mδ0
в левой части которого погрешность нуля 6о суммируется один раз (все разряды включены), а в правой— т раз (m отдельных считываний выходного сигнала ЦАП). При этом погрешность измерения нелинейности будет меньше, если смещение нуля 6о запоминается и вычитается из напряжения каждого последующего считываемого разряда до того, как будет произведено определение нелинейности.
Абсолютная погрешность преобразования отражает отклонение фактического выходного сигнала преобразователя от теоретического, вычисленного для идеального преобразователя. Этот параметр указывается обычно в процентах к полной шкале преобразования и учитывает все составляющие погрешности преобразования (нелинейность, смещение нуля, коэффициент преобразования). Поскольку абсолютное значение выходного сигнала преобразователя определяется опорным напряжением Uoп [см. соотношения (3), (4)], то абсолютная погрешность преобразования находится в прямой зависимости от стабильности напряжения Uоп. В большинстве преобразователей используется принцип двойного кодирования. Поэтому для получения кратного значения младшего разряда обычно выбирают Uon= 10,24 В. В этом случае для 12-разрядных ЦАП расчетное номинальное значение младшего разряда Δ=2,5 мВ и напряжение полной шкалы Uп.ш.н= 2,5 (212—1) мВ= 10237,5 мВ.
Изменение напряжения Uon, например, на 1% вызовет изменение абсолютной погрешности преобразования также на 1%, что составит в верхней точке диапазона 102,375 мВ.
Дифференциальная нелинейность δн.д определяется отклонением приращения выходного сигнала преобразователя от номинального значения младшего разряда при последовательном изменении кодового входного сигнала на единицу. Дифференциальная нелинейность идеального преобразователя равна нулю. Это означает, что при изменении входного кода преобразователя на единицу его выходной сигнал изменяется на значение младшего разряда. Допустимым значением дифференциальной нелинейности считается (1/2)[ПВ1] Δ(1/2 значения младшего разряда).
Дифференциальная нелинейность может быть вычислена таким образом. Для конкретного m-разрядного преобразователя расчетное значение единицы младшего разряда Δр=[Uп.ш/(2m—l).
обеспечивающее контроль схем различного назначения, обычно сложное и дорогостоящее. Установки специального назначения, контролирующие схемы, как правило, одного типа, выполняют контроль быстрее, и с ними могут работать люди, не обладающие большим опытом и мастерством.
В преобразователях с высокой разрешающей способностью необходимо проконтролировать большое количество параметров для получения информации о работе преобразователя. Например, 12-разрядный ЦАП или АЦП имеет 212, или 4096, возможных комбинаций вход— выход. Безусловно, без применения автоматизированной высокопроизводительной установки решить проблему контроля подобных преобразователей невозможно.
При контроле ИМС АЦП, особенно многоразрядных, необходимо соблюдать меры предосторожности при подключении контролируемого преобразователя к установке контроля. Линии связи должны быть такой длины и такого сопротивления, чтобы падение напряжения на них не вызвало значительного увеличения погрешности измерения параметров ИМС АЦП.
Если проверяют ЦАП с токовым выходом, то к его выходу подключают операционный усилитель, обеспечивающий преобразование выходного тока ЦАП в напряжение. При этом резистор обратной связи, входящий в состав ЦАП, подключают без подстроечных потенциометров, чтобы можно было измерить погрешность смещения нуля и полной шкалы.
Далее перед измерением параметров ЦАП нужно определенное время для его прогрева, чтобы обеспечить установившийся тепловой режим контроля. Это относится в первую очередь к контролю нелинейности ЦАП, поскольку требуется большое количество измерений, за время которых из-за нагрева ЦАП его параметры могут существенно измениться. Например, у ЦАП с рассеиваемой мощностью порядка 500 мВт время прогрева в зависимости от типа корпуса колеблется от 5 до 15 мин.
С целью уменьшения времени контроля желательно проводить контроль параметров ЦАП не во всех точках его выходной характеристики. Минимальный объем получаем при контроле значений всех разрядов, включаемых по одному. Однако такой контроль допустим только в случае малого взаимного влияния разрядов, когда все разряды или комбинации разрядов, которые включаются, полностью независимы от включенного (выключенного) состояния других разрядов. В противном случае для получения достоверного результата следует производить контроль по всем дискретным значениям выходного сигнала, т. е. в 2mочках характеристики.
Далее будут рассмотрены методы контроля статических и динамических параметров ИМС АЦП, которые могут быть использованы в автоматизированных системах контроля, предназначенных как для обеспечения серийного производства ИМС АЦП, так и для их входного контроля.
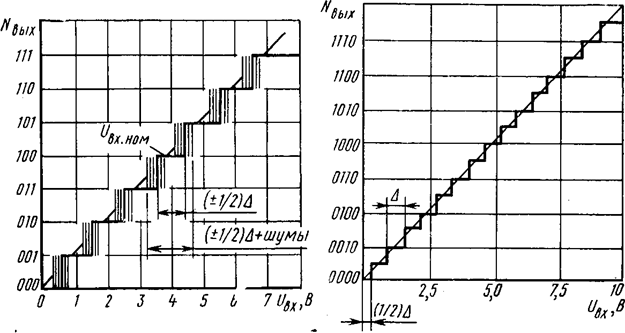
Рис. 4. Характеристика АЦП при наличии шума Рис. 5. Характеристика идеального четырехразрядного АЦП