Парная корреляция - это связь между двумя показателями, один из которых является факторным, а другой - результативным. Множественная корреляция возникает от взаимодействия не скольких факторов с результативным показателем
Коэффициент парной корреляции является безразмерным нормированным корреляционным моментом. Коэффициенты парной корреляции характеризуют тесноту связи между двумя показателями в общем виде с учетом взаимосвязей факторов, оказывающих воздействие на результативный показатель.
индекс множественной корреляции

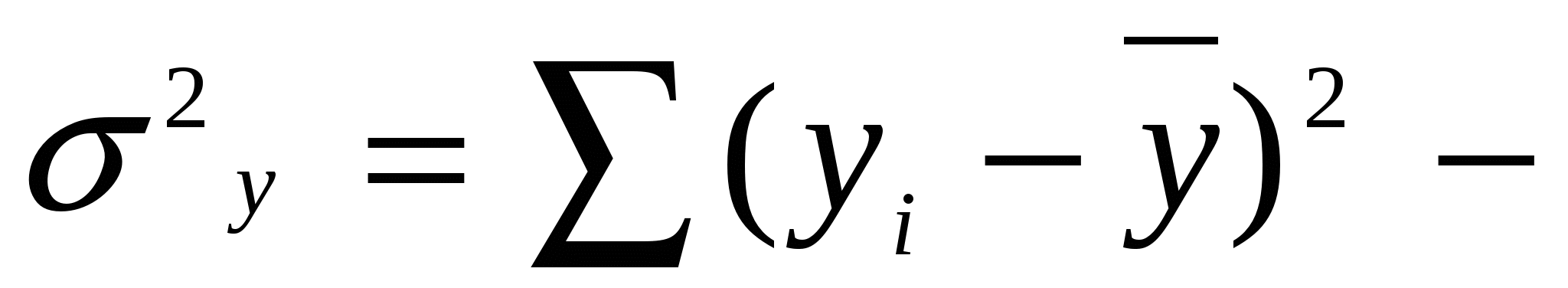 общая дисперсия результативного признака
общая дисперсия результативного признака
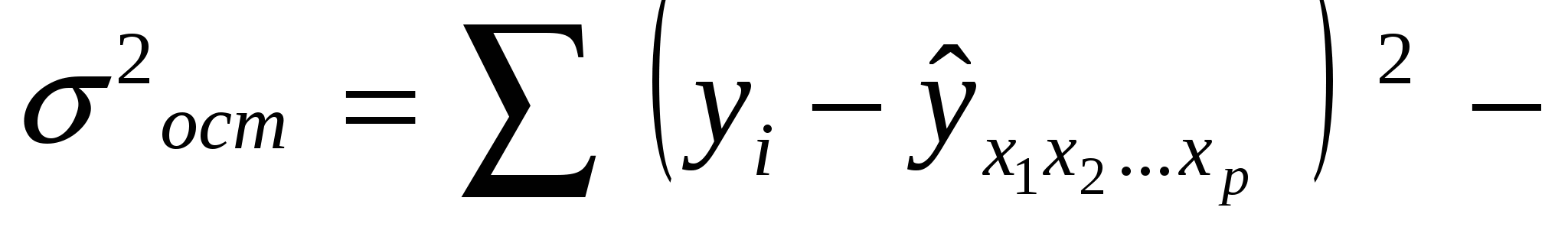 остаточная дисперсия для уравнения с полным набором факторов
остаточная дисперсия для уравнения с полным набором факторов
Коэффициент (или индекс) множественной детерминации оценивает качество построенной модели в целом и рассчитывается как квадрат индекса множественной корреляции или квадрат совокупного коэффициента множественной корреляции:

Частные коэффициенты (или индексы) корреляции

Средние коэффициенты эластичности
 Для линейной множественной регрессии
Для линейной множественной регрессии

Ранговая корреляция и непараметрические методы измерения связей
Ранговая корреляция-мера зависимости между случайными величинами, когда эту зависимость невозможно определить количественно с помощью обычного коэффициента корреляции. Процедура установления Р. к. заключается в упорядочении изучаемых объектов в отношении некоторого признака, т. е. им приписываются порядковые номера. Наиболее распространен коэффициент Р. к. (коэффициент Спирмэна):
 где Di — разница между рангами, присвоенными каждой из переменных N — размер выборки. Этот коэффициент принимает значения между +1 и –1, показывая тесноту и направление связи между исследуемыми величинами. Метод Р. к. — один из т. н. непараметрических методов математической статистики. Для оценки тесноты связи между качественными показателями применяют непараметрические методы оценки корреляционной связи факторов. К непараметрическим методам относятся оценка связи на основе расчета коэффициентов ассоциации и контингенции. Для этого предварительно составляют таблицу, на пересечении строк и столбцов которой находятся числа, равные количеству единиц статистической совокупности с соответствующими значениями первого и второго признака.
где Di — разница между рангами, присвоенными каждой из переменных N — размер выборки. Этот коэффициент принимает значения между +1 и –1, показывая тесноту и направление связи между исследуемыми величинами. Метод Р. к. — один из т. н. непараметрических методов математической статистики. Для оценки тесноты связи между качественными показателями применяют непараметрические методы оценки корреляционной связи факторов. К непараметрическим методам относятся оценка связи на основе расчета коэффициентов ассоциации и контингенции. Для этого предварительно составляют таблицу, на пересечении строк и столбцов которой находятся числа, равные количеству единиц статистической совокупности с соответствующими значениями первого и второго признака.
| Первый признак | Второй признак | ||
| Первое значение | Второе значение | Итого | |
| Первое значение | а | b | а+b |
| Второе значение | с | d | c+d |
| Итого | а+с | b+d |
По итоговым данным таблицы 1 рассчитывают коэффициент ассоциации либо коэффициент контингенции:

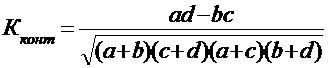
Если эти коэффициенты < 0.3, то связи между признаками нет. Преимущество первого показателя состоит в том, что он единственный из всех показателей тесноты связи вполне определенно позволяет ответить на вопрос о характере связи между двумя признаками (прямопропорциональна она или обратнопропорциональна).