Рисунок 3.2. Структурный анализ.
Так как наивысший класс присоединенной группы Ассура – второй, то
механизм относится ко второму классу.
Формула строения механизма:
Определение геометрических размеров рычажного механизма.
Исходные данные:
ход поршня H=0,124м;
частота вращения карданного вала n1=2050об/мин;
максимальный угол давления между шатуном и поршнем 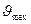 =12,50;
=12,50;
диаметр поршня d=0,084м;
частота вращения карданного вала 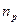 =180 об/мин.
=180 об/мин.
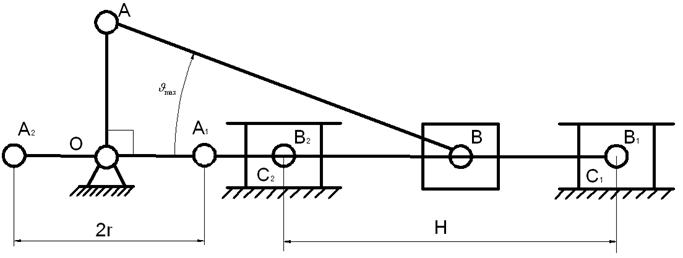
Рисунок 3.3. Положения механизма в крайних точках и при максимальном угле давления.
На Рисунке 3.3. изображен механизм в крайних положениях с указанием хода поршня – H, и положение механизма при котором имеет максимальное значение угол давления.
Найдем длину кривошипа:
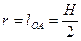
где 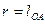 - длина кривошипа; Н- ход поршня.
- длина кривошипа; Н- ход поршня.
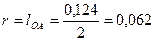 м.
м.
Найдем длину шатуна из отношения при максимальном угле давления:
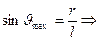
 .
.
где 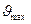 - максимальный угол давления шатуна;
- максимальный угол давления шатуна;  - длина шатуна.
- длина шатуна.
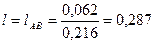 м.
м.
Положение центров масс звеньев механизма:
Так как кривошип уравновешен, то центр масс лежит в точке О - 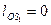 .
.
Центр масс шатуна находится в точке  на линии АВ:
на линии АВ:
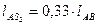
где 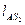 - расстояние от точки А до центра масс шатуна.
- расстояние от точки А до центра масс шатуна.
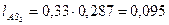 м.
м.
Центр масс ползуна находится в точке В - 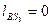 .
.
Массы звеньев:
m2=q lАВ
где q- масса одного метра звена; m2- масса шатуна.
m2= 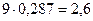 кг.
кг.
m3=0,8 m2
где m3-масса поршня.
m3=  кг.
кг.
m1=3,8 m2
где m1- масса кривошипа.
m1=  кг.
кг.
Осевые моменты инерции звеньев:
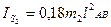
где  - осевой момент инерции шатуна.
- осевой момент инерции шатуна.
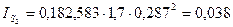 кгм2.
кгм2.

где  - осевой момент инерции кривошипа.
- осевой момент инерции кривошипа.
 кгм2.
кгм2.
Средняя угловая скорость кривошипа определяется по формуле:
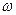 1ср=
1ср= 
где 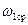 - средняя угловая скорость кривошипа.
- средняя угловая скорость кривошипа.
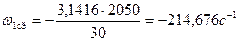
Таблица 3.1. Результаты расчета геометрических характеристик механизма.
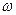 1ср,
1/c 1ср,
1/c
| Размеры l,м | Массы,кг | Осевые моментыинерции Is, кгм2 | |||||
| lОА | lАВ | lAS2 | m1 | m2 | m3 | 
| 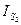
| |
| -214,676 | 0,062 | 0,287 | 0,095 | 9,8 | 2,6 | 2,1 | 0,019 | 0,038 |
Расчет кинематических характеристик рычажного механизма.
|
|
Графический метод.
3.4.1. Построение планов положения механизма.
После завершения расчета геометрических размеров приступаем к построению планов положений механизма.
Для построения планов положений механизма необходимо определить масштабный коэффициент, используя который реальные размеры звеньев выражаются в отрезках, изображаемых на чертеже.
Для этого примем ОА=40 мм, тогда

где 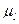 - масштабный коэффициент; ОА-отрезок на чертеже эквивалентный
- масштабный коэффициент; ОА-отрезок на чертеже эквивалентный  .
. 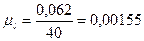 м/мм.
м/мм.
Примем масштабный коэффициент 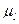 =0,001 м/мм.
=0,001 м/мм.
Определим величины OA,АВ и АS2:
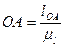
Где OA-отрезок на чертеже равный  .
.
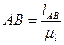
где АВ - отрезок на чертеже равный  .
.
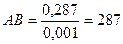 мм.
мм.
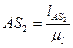
где АS2 - отрезок на чертеже равный 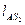 .
.
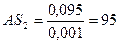 мм.
мм.
Для построения плана положений необходимо выбрать точку О и провести окружность радиусом ОА. Разбиваем окружность на 12 равных частей(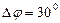 ).
).
Нумеруем полученные точки и соединяем их с центром О. Полученные точки являются планом положений кривошипа.
Из построенных на окружности точек проводим отрезки длиной АВ до пересечения их с осью ОХ. Полученные точки нумеруем в соответствии с нумерацией точек на окружности. Полученные точки являются планом положений ползуна, а отрезки - шатуна.
На плане положений шатуна от точек Аi откладываем отрезки длиной АS  i, и полученные точки нумеруем соответственно точкам на окружности. Данные точки будут являться положениями центра массы шатуна.
i, и полученные точки нумеруем соответственно точкам на окружности. Данные точки будут являться положениями центра массы шатуна.
|
|
Выполняем замеры и пересчет контрольных параметров:
- угол положения шатуна φ2=349 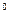 ;
;
- координата ползуна хB= 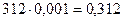 м;
м;
- координаты центра масс шатуна xS2= 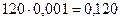 м, yS2=
м, yS2= 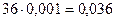 м;
м;
- перемещение ползуна SB= 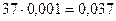 м.
м.
3.4.2. Построение плана аналогов скоростей (в одном контрольном положении).
Для построения плана аналогов скоростей выбираем контрольное положение. Это положение в котором угол φ1=600.
Скорость точки А кривошипа определяется по формуле:
VA= 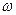 1lОА
1lОА
где VA - скорость точки А кривошипа.
По формуле для определения аналога скорости  :
:

где  -аналог скорости точки А.
-аналог скорости точки А.
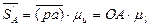
где  - вектор на плане аналогов скоростей;
- вектор на плане аналогов скоростей;  - масштабный коэффициент плана аналогов скоростей.
- масштабный коэффициент плана аналогов скоростей.
Выберем 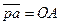 , тогда
, тогда 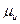 =
= 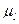 =0,001 м/мм;
=0,001 м/мм;
Строим на чертеже точку p – полюс плана аналогов скоростей. Проводим из точки p отрезок pa перпендикулярный OA и направленный в сторону вращения кривошипа (аналог скорости совпадает по направлению с вектором скорости).
Аналог скорости точки А – отрезок ра=OA =62мм.
Для точки В записываем систему векторных уравнений:

где 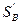 - аналог скорости точки В;
- аналог скорости точки В; 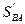 - аналог скорости точки В относительно точки А,
- аналог скорости точки В относительно точки А,  ;
;  - аналог скорости точки В относительно точки
- аналог скорости точки В относительно точки  ,
, 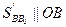 ;
; 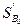 - аналог скорости точки
- аналог скорости точки  ,
, 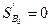 .
.
Из точки a строим прямую линию перпендикулярную шатуну АВ плана положений механизма. Из точки р строим прямую линию параллельную оси OX плана положений механизма. На пересечении этих линий получаем точку b.
Точку S2 на плане строим исходя из теоремы подобия аналогов скоростей:
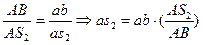
где ab – отрезок на плане аналогов скоростей; 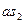 - расстояние до точки
- расстояние до точки  на плане аналогов скоростей.
на плане аналогов скоростей.
|
|
 мм.
мм.
Расчет первых передаточных функций механизма.
Для определения первых передаточных функций необходимо на плане аналогов скоростей замеряем следующие параметры:
ps2=59,4 мм;
xs2=55,7 мм;
ys2= - 20,7мм;
ab=31,6 мм;
pb=59,7 мм;
Определяем первую передаточную функцию ползуна 3(точка В):
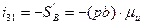
где 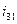 - первая передаточная функция ползуна;
- первая передаточная функция ползуна; 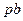 - отрезок на плане аналогов скоростей.
- отрезок на плане аналогов скоростей.
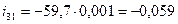 м.
м.
Определяем первую передаточную функцию шатуна 2:
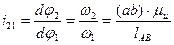
где 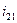 - первая передаточная функция шатуна;
- первая передаточная функция шатуна;  - угловая скорость шатуна.
- угловая скорость шатуна.
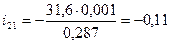
Определяем первую передаточную функцию точки  :
:
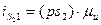
где  - первая передаточная функция центра масс шатуна;
- первая передаточная функция центра масс шатуна; 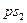 - отрезок до точки
- отрезок до точки  на плане аналогов скоростей.
на плане аналогов скоростей.
 м.
м.
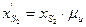
где  - координата центра масс шатуна на плане аналогов скоростей по оси ОХ;
- координата центра масс шатуна на плане аналогов скоростей по оси ОХ; 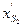 - координата центра масс шатуна.
- координата центра масс шатуна.
 м.
м.
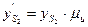
где  - координата центра масс шатуна на плане аналогов скоростей по оси ОY;
- координата центра масс шатуна на плане аналогов скоростей по оси ОY; 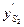 - координата центра масс шатуна.
- координата центра масс шатуна.
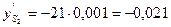 м.
м.
Аналитический метод.