С помощью зависимости 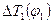 , используемой при определении постоянной составляющей приведенного момента инерции
, используемой при определении постоянной составляющей приведенного момента инерции 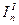 по методу Мерцалова, можно получить зависимость угловой скорости звена приведения
по методу Мерцалова, можно получить зависимость угловой скорости звена приведения 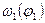 .
.
Из Рисунка 3.7. видно, что для любого положения кинетическая энергия звеньев, обладающих постоянным приведенным моментом инерции 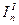 равна:
равна:
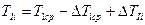
где 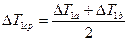 ,
, 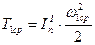 .
.
Так как 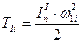 , то текущее значение угловой скорости
, то текущее значение угловой скорости
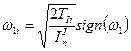
Угловое ускорение 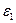 определяется из дифференциального уравнения движения звена приведения:
определяется из дифференциального уравнения движения звена приведения:
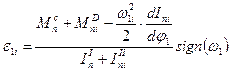
Схема алгоритма программы исследования динамической нагруженности машинного агрегата
Рассмотренные в предыдущих пунктах материалы позволяют разработать программу исследования динамической нагруженности машинного агрегата. В качестве объекта исследования взята технологическая машина, в которой основным исполнительным механизмом является кривошипно-ползунный механизм. Примерная схема приведена на Рисунке 3.9.
Осуществляется ввод исходных данных. Следует обратить внимание на соответствие направления вращения кривошипа 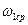 , знака
, знака 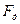 по отношению к положительному направлению соответствующей оси координат, а также на знак величины эксцентриситета e.
по отношению к положительному направлению соответствующей оси координат, а также на знак величины эксцентриситета e.
В следующем блоке вычисляется угловой шаг 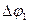 , max координата ползуна
, max координата ползуна  и присваивается начальное значение обобщенной координате
и присваивается начальное значение обобщенной координате 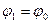 .
.
Далее в цикле по 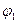 вычисляются кинематические характеристики рычажного механизма, динамические характеристики рычажного механизма, динамические характеристики
вычисляются кинематические характеристики рычажного механизма, динамические характеристики рычажного механизма, динамические характеристики 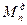 ,
, 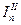 ,
, 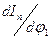 , кинетическая энергия ТII, работа сил сопротивления Ас.
, кинетическая энергия ТII, работа сил сопротивления Ас.
По окончании цикла определяется приведенный момент сил сопротивления 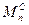 .
.
В новом цикле производится вычисление А 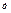 ,
, 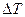 ,
, 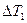 .
.
В подпрограмме из массива 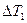 находятся экстремальные значения
находятся экстремальные значения 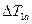 и
и 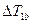 , что позволяет в блоке 14 определить величины
, что позволяет в блоке 14 определить величины 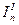 ,
,  , а также
, а также 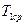 и
и 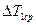 .
.
|
|
После вычисления в цикле 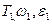 производится печать результатов расчета.
производится печать результатов расчета.
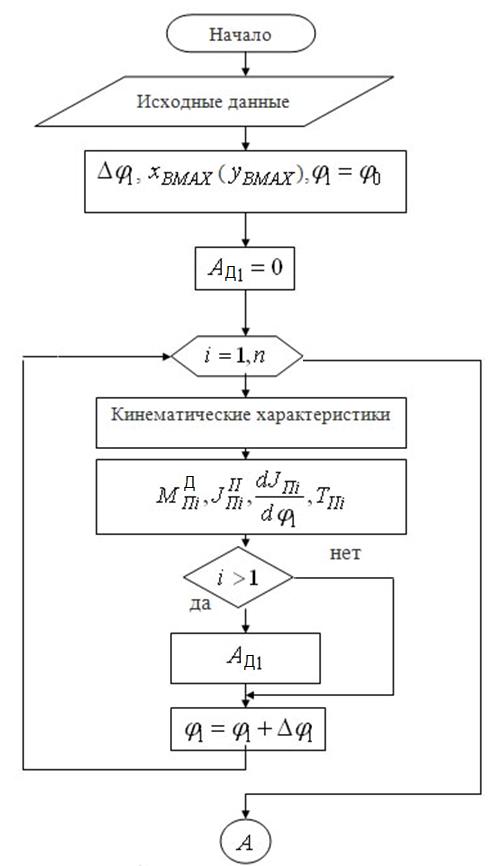
Рисунок 3.8. Схема алгоритма программы
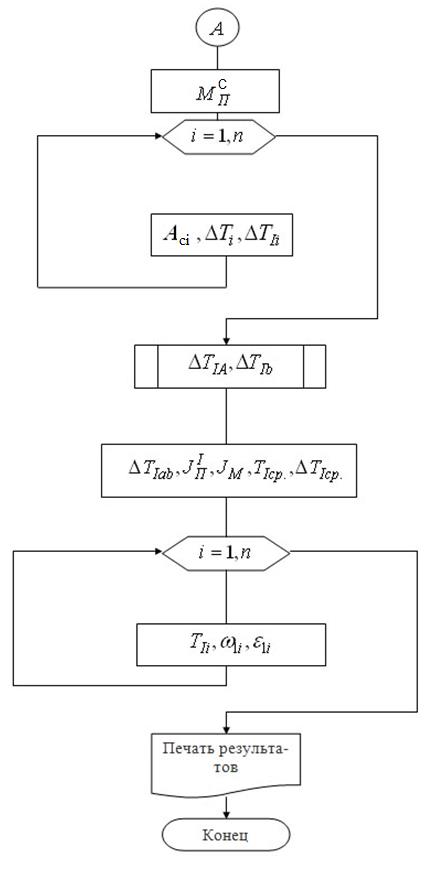
Окончание Рисунка 3.8.
Подготовка исходных данных для ЭВМ и расчет на ЭВМ.
В таблице 3.5. представлены исходные данные, необходимые для расчетов на ЭВМ.
Таблица 3.5. Исходные данные для ЭВМ.
| № | Параметр | Условное обозначение | Единица измерения | Величина |
| Схема кривошипно-ползунного механизма | – | – | 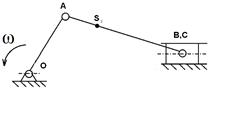
| |
| Размеры звеньев | 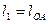
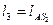
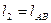
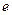
| м м м м | 0,062 0,095 0,287 | |
| Начальная обобщенная координата | 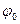
| град | ||
| Массы и моменты инерции звеньев | 
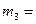
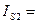
| кг
кг

| 2,6 2,1 0,038 | |
| Движущая сила | 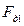

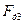
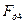
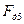
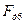
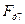
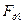
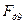
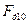
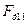
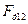
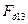
| Н Н Н Н Н Н Н Н Н Н Н Н Н | -31018 -26587 -17725 -9416 -8309 -2216 -1662 -5262 -9693 -13294 | |
| Средняя угловая скорость кривошипа | 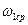
| рад/с | 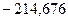
| |
| Коэффициент неравномерности вращения вала кривошипа | 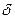
| 0,015 | ||
| Приведенный к кривошипу момент инерции всех вращающихся звеньев | 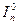
| 
| 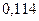
|
Построение графических зависимостей по результатам Приложения 1.
Построение графика кинематических характеристик ползуна.
Кинематическими характеристиками ползуна 3 являются перемещение, первая и вторая передаточные функции. Масштабный коэффициент принимаем равным μ  =μs=μi=μi'=0,001м/мм. Масштабный коэффициент угла положения φ для всех графиков принимаем μφ=2град/мм.
=μs=μi=μi'=0,001м/мм. Масштабный коэффициент угла положения φ для всех графиков принимаем μφ=2град/мм.
Таблица 3.6. Координаты для построения графиков кинематических характеристик ползуна.
| Переменная | |||||||||||||
| ySB | 36,1 | 68,8 | 98,1 | 117,4 | 123,7 | 117,4 | 98,1 | 68,8 | 36,1 | ||||
| yi | 36,8 | 59,6 | 47,8 | 25,2 | -25,2 | -47,8 | -62 | -59,6 | -36,8 | ||||
| yi' | -75 | -61 | -24 | -24 | -61 | -75 |