Интеграл Кирхгофа
Как уже говорилось ранее при расчете звуковых полей, излучаемых колеблющимися поверхностями, возникает необходимость вычисления потенциала поля 
в некоторой области пространства по значению потенциала и его нормальной производной (т.е. по значению звукового давления и колебательной скорости) на заданной поверхности. Рассмотрим произвольную область, ограниченную поверхностью S, представленную на рис 3.11.
Рис. 3.11
Требуется найти связь между значением 
в некоторой области пространства V для точки наблюдения (.) М и значением Ф на поверхности S. Такая связь может быть получена путем использования формулы Грина, связывающей значения объемного и поверхностного интегралов.
Формула Грина записывается следующим образом: любые две функции и 
, непрерывны вместе со своими первыми и вторыми производными в объеме V, удовлетворяют соотношению.
. (3.46)
В этой формуле n – внешняя нормаль. Пусть внутри объема V существует два звуковых поля, описываемых функциями и , которые удовлетворяют уравнению Гельмгольца:
. (3.47)
Звуковое поле – это основное поле, которое требуется определить; поле является вспомогательной величиной. Звуковое поле в уравнении Гельмгольца (3.) умножим на , а второе уравнение - на , затем вычтем второе уравнение из первого и сумму проинтегрируем по объему V.
В результате получим соотношения:
. (3.48)
Применяя к последнему выражению формулу Грина, можно записать:
. (3.49)
Вспомогательной функцией может быть любая функция, удовлетворяющая уравнению Гельмгольца и сформулированным выше требованиям непрерывности в объеме V. Выберем в качестве поле точечного ненаправленного источника, помещенного в точке наблюдения М.
(3.50)
где 
, 
- радиус вектор, проведенный от начала координат в точку наблюдения М; 
- радиус вектор, направленный в любую точку поля.
В сферической системе координат в силу симметрии задачи уравнение Гельмгольца можно записать в виде:
. (3.51)
Прямой подстановкой легко установить, что функция 
удовлетворит этому уравнению.
Это утверждение справедливо для всех точек области V, за исключением точки 
. В точке функция имеет особенность, и дифференцировать ее в этой точке невозможно. Кроме того, для функции неверна и формула Грина, т.к. она справедлива лишь для функций, непрерывных во всех точках области. Поэтому точку наблюдения надо исключить из рассматриваемой области. Для этого окружим точку М малой сферой 
радиуса а. Новая область будет расположена между 
и , а полная новая поверхность, ограничивающая объем, будет состоять из двух частей и .
Рассмотрим интеграл по поверхности . Наружная к области нормаль к поверхности будет направлена внутрь сферы . Из-за этого на имеем 
. Сколь бы малым ни выбиралось значение радиуса окружности - а, величины и 
на поверхности будут оставаться конечными, так что применение формулы Грина является допустимым.
Вычислим:
. (3.52)
Поскольку искомое поле является непрерывной функцией координат в любой точке области, то в пределах малой сферы радиуса а, можно считать, что и 
мало зависит от положения точки на поверхности 
. Поэтому и можно вынести из под знака интеграла, заменив их значения в точке, определенной вектором 
. Для функции этого сделать нельзя, так как внутри она обладает особенностью.
В результате можно записать:
.
Учитывая, что на поверхности :
,
где 
– элемент телесного угла, получим:
.
Отметим, что поверхность интегрирования является суммой S и . Тогда получим, что 
, откуда:
. (3.53)
Так как интегрирование проводится по поверхности , то величины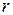 
в этой формуле являются расстоянием от точки наблюдения М до элемента 
поверхности S.
Полученное выражение (3.53) носит название формулы Кирхгофа или интеграла Кирхгофа.
Использование полученной формулы для практических расчетов тоже затрудняется тем обстоятельством, что на излучающей поверхности обычно известна одна из величин и . Если колебательная скорость 
(или ) на поверхности задана, то звуковое давление пропорциональное потенциалу Ф, как правило, оказывается неизвестным. Поэтому неизвестная величина будет входить и в левую и в правую части уравнения (3.53). Фактически формула (3.53) и является интегральным уравнением. В ряде случаев удается из физических соображений указать хотя бы приближенную связь между величинами Ф и .
Тогда интеграл Кирхгофа определяет приближенное решение задачи излучения им дифракции звука. Если поверхность S представляет собой плоскость, то интеграл Кирхгофа удается свести к формулам, которые дают точные решения для случаев, когда на поверхности оказывается известной лишь одна из величин Ф и . Такие формулы называются интегральными формулами Гюйгенса.
Рассмотрим излучение бесконечной плоскости S в верхнее полупространство. 
Дополним плоскость до замкнутой поверхности полусферой 
(рис. 3.12).
При увеличении радиуса полусферы интеграл по 
должен стремиться к нулю в силу принципа 
излучения. Поэтому при использовании формулы Грина можно ограничиться интегрированием по плоскости. Запишем формулу интеграла Кирхгофа в виде.
. (3.54)
где U – вспомогательная функция, представляющая собой поле точечного источника. Выберем в (3.54) в качестве U функцию, которая описывает поле точечного источника, расположенного над абсолютно жесткой поверхностью.
Рис. 3.12
Очевидно, что в точке М поле от источника, помещенного в произвольную точку над плоскостью может быть представлено в виде суммы полей источника 
и зеркально расположенного источника 
:
. (3.55)
Нормальная производная этого поля определяется выражением:
. (3.56)
Устремим точку Q к границе. Учитывая, что на границе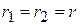 
, 
, получим 
. Подставляя эти значения (3.55, 3.56) в формулу (3.54), получим:
. (3.57)
Выражение (3.57) называется первой интегральной формулой Гюйгенса. Важным преимуществом этой формулы по сравнению с интегралом Кирхгофа является то, что здесь для расчета звукового поля во всем полупространстве требуется знать только одну величину , т.е. колебательную скорость поверхности. Перейдем от потенциалов к колебательной скорости и звуковому давлению: 
; 
. Тогда:
(3.58)
Полученное выражение (3.57) служит основной формулой для расчета звуковых полей плоских излучателей и приемников звука. Формально эти выражения являются точными, однако при их применении колебательная скорость должна быть известна на всей поверхности S. Реальные излучающие поверхности ограничены, поэтому при расчете звуковых полей плоских излучателей их излучающая поверхность дополняется абсолютно жестким экраном, на котором можно положить 
.
Для того, чтобы получить вторую интегральную формулу Гюйгенса, следует в качестве вспомогательной функции выбрать поле точечного, ненаправленного источника, расположенного над абсолютно мягкой поверхностью. В этом случае поле мнимого источника будет противоположно по знаку полю источника :
. (3.59)
Вычислив производную от (3.59) и устремив точку Q к границе, получаем: 
. Тогда:
. (3.60)
Вместо потенциалов в (3.60), по аналогии с (3.58) легко перейти к звуковым давлениям.
Это выражение (3.60) и есть вторая интегральная формула Гюйгенса, определяющая значения звукового давления в полупространстве по известной величине звукового давления на плоскости.
Как и ранее, для ограниченных участков плоскости, излучатель конечных размеров следует дополнить до бесконечной плоскости «абсолютно мягким экраном», на котором можно задать условие Ф = 0. Тогда интегрирование нужно проводить только по поверхности излучателя.
Эффект Доплера
При информационном обмене в акустических полях существенно важным является то, в каком состоянии находятся источники и приемники излучения относительно друг друга. Причем если они перемещаются, то важно знать, с какой скоростью и направлением. На практике и путем проведения большого числа экспериментов было установлено, что частоты излучаемого и принимаемого сигнала могут сильно отличаться друг от друга. Для этого отличия можно дать качественные и количественные описания, рассмотрев для стройности изложения четыре частных случая.
Итак, эффект Доплера заключается в том, что в результате взаимного перемещения источника и приемника звука относительно неподвижной акустической среды, частота сигнала, фиксируемая приемником, отличается от частоты сигнала, излученного источником.
Случай 1. Источник движется, приемник неподвижен.
Для простоты рассмотрим два точечных источника и приемника, обменивающихся гармоническим сигналом. Пусть источник звука –излучатель (И) движется из точки А в точку Б, как показано на рис 3.13. Движение И происходит со скоростью Vизл под углом j относительно линии соединения точек А и Б.
Рис. 3.13
Допустим, что при нахождении излучателя И в точке А им создано сжатие, которое в некоторый момент времени достигло точки Б, т.е. приемника. В дальнейшем источник, двигаясь в указанном направлении, периодически создаёт сжатие и разрежение среды, которые в направлении от (∙) А и (∙) Б будут сближаться, а в направлении от (∙) Б к (∙) А (слева от точки (.) А)– удаляться друг от друга.
Это изменение будет тем заметней, чем больше скорость движения источника. При неподвижном излучателе и приемнике расстояния между созданными областями сжатия и разрежения соответствует длине волны λ. Если излучатель перемещается, то приемник будет реагировать на измененную длину волны и более короткую, чем приемники, расположенные по всем другим направлениям по сравнению с φ=0. Это можно записать, как: 
, где с - скорость звука. Ясно, что при φ≠0:
. (3.61)
Поскольку 
, то из (3.61) можно записать:
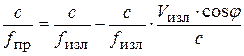, или 
. (3.62)
Домножим правую часть (3.62) на знаменатель с обратным знаком и, тогда:
.
Т.к., обычно 
, когда скорость движения излучателя значительно меньше скорости звука в среде, то приближенно:
. (3.63)
Сразу видно (из 3.63), что частота реагирования приемника существенно отличается от частоты излучения. Отметим, что при j = 0, когда V изл ®С, то f пр®¥, что на практике невыполнимо, так как движение на «дозвуковых» и «сверхзвуковых» скоростях сопровождается другими эффектами. Принято говорить, что эффект Доплера в рассмотренном случае физически обусловлен “деформацией” акустического поля за счет движения источника. Ясно, что для сохранения величины частоты принимаемого сигнала источник должен двигаться по «круговой» траектории.
Случай 2. Источник неподвижен, приемник перемещается
В отличие от предыдущего случая, т.к. при движении приемника никакой деформации излучаемого поля не происходит, то приемник просто с большей частотой встречается с волновыми фронтами (см. рис. 3.14).
Рис. 3.14
Можно показать, что по сравнению с формулой (3.63) получаемое для определения частоты принимаемого сигнала равенство является строгим:
. (3.64)
Поэтому при q = 0 и 
® с, частота принимаемого сигнала стремится к удвоенному значению по сравнению с частотой излучаемого сигнала. Ясно, что при движении и приемника по нормали к направлению отрезка, соединяющего точки расположения излучателя и приемника (по «кругу»), частота принимаемого сигнала изменяться не будет (q = 90°).
Случай 3. Источник и приемник подвижны.
Их взаимное расположение относительно системы координат представлено на рис. 3.15. В этом случае сигналы, поступающие от обоих объектов, перемножаются и для частоты приема можно на основании результатов, полученных для двух предшествующих вариантов, записать точное соотношение:
. (3.65)
Рис. 3.15
Очевидно, что при малости скорости движения излучателя по сравнению со скоростью звука: 
, тогда (3.65) превратится в:
.
Раскрываем скобки и, учитывая 
, получим:
. (3.66)
Таким образом, отклонение частоты носит знакопеременный характер. Его величина определяется формулой:
. (3.67)
Максимальное отклонение частоты по (3.67) при φ=0, q = 180º и φ=180º, q = 0 составит:
.
Пример: Для звуковой волны, распространяющейся в воде с = 1500 м/с. Если 
= 10 м/с, то при 
Гц максимальное отклонение частоты (по формуле 3.67) составит:
.
Ясно, что изменения величины частоты принимаемого сигнала не будет, когда излучатель и приемник будут двигаться по масштабно подобным траекториям (например, параллельно друг другу).
Случай 4. Эхолокация (И + П – совмещены на подвижном носителе, цель – осуществляет перемещение).
Схема образования информационных сигналов при взаимодействии подвижного совмещенного излучателя – приемника с отражающей целью представлена на рис. 3.16.
Рис. 3.16
При приеме эхо-сигнала изменение частоты из-за эффекта Доплера будет выражено более сильно, чем при прямом обмене. Причина этого в том, что падение акустической волны на препятствие и отражение от него можно отождествить с излучением и приемом «вторичных» волн. Тогда частота принимаемого эхосигнала может быть определена возведением в квадрат сомножителей, определяющих изменяющиеся частоты для подвижных излучателей и приемников по отдельности.
Тогда точным выражением для изменения частоты сигнала будет:
. (3.68)
Пренебрегая в (3.68) величинами второго порядка малости, по аналогии с вышеуказанными случаями, получим для частоты принимаемого сигнала, с учетом 
:
. (3.69)
Тогда, с учетом (3.69) максимальное отклонение частоты:
. (3.70)
Указанное выражение (3.70) чаще всего используется на практике для оценки полосы пропускания электронных трактов аппаратуры специального и другого назначения.
Подведем итоги…
· Отношение величины звукового давления и колебательной скорости в поле звуковой волны является постоянной величиной, равной произведению плотности среды на скорость звука, и называемой волновым сопротивлением среды;
· Помимо импедансов прилегающих сред, существуют и другие параметры (скорость относительного перемещения, степень нарушения адгезионной связи на границе и др.), которые необходимо учитывать при согласовании числа независимых измерений для решения прямых и обратных задач акустических измерений; подбирая величины импедансов и других параметров можно синтезировать «неотражающие» звук препятствия;
· Величины углов падающей, отраженных и преломленных волн пропорциональны скоростям звука в соответствующих средах и определяются законом Снеллиуса; При определенных соотношениях скоростей звука возможно образование явления «полного внутреннего отражения», которое сопровождается возникновением «критических углов.
· Помимо величин рассеянного поля при информационном обмене важно учитывать и относительное (друг к другу) движение источников и приемников звука