Рассмотрим процесс отражения плоской упругой волны на плоскостной границе двух (жидких или газообразных) сред. Требуется получить аналитическое выражение для коэффициентов отражения и прохождения по давлению и колебательной скорости.
Рис. 3.5
Рассмотрим падение плоской волны в плоскости ХУ, в системе координат, представленной на рис. 3.5. Запишем аналитические выражения для всех волн, образующихся при наклонном падении:
,
, 
, (3.13)
На плоской границе раздела должны выполняться граничные условия, характеризующие равновесие действующих сил и выполнение условий «сплошности» среды. Поле давления, действующего впервой среде: 
. Поле давления во второй среде: 
.
Граничное условие первого типа:
1. Равенство давлений по обе стороны границы
. (3.14)
Граничное условие второго типа:
2. Равенство нормальных компонент упругих смещения и колебательных скоростей, с учетом 
:
. (3.15)
Для удобства вычислений безразмерных выражений введем дополнительные обозначения:
, (3.16)
коэффициент отражения по давлению;
, (3.17)
коэффициент прохождения по давлению.
Подставив полученные выражения для системы волн в граничные условия, получим систему двух уравнений с двумя неизвестными R и D.
Решение этой системы: при 
- «нормальное» падение:
, (3.18)
. (3.19)
При этом было учтено, что по закону Снеллиуса:
(3.20)
Если в выражениях (3.18, 3.19) перейти к колебательным скоростям, то можно получить выражения для коэффициентов отражения 
и прохождения 
по колебательной скорости:
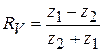, (3.21)
. (3.22)
Видно, что эти выражения имеют разный характер, что подчеркивается разным физическим смыслом величин давления и колебательной скорости в звуковом поле. Выражения для коэффициентов отражения и прохождения по потенциалу подобны выражениям для коэффициентов по давлению. Выражения для коэффициентов отражения по упругим смещениям подобны выражениям коэффициентов отражения и прохождения по колебательной скорости.
Рассмотрим частные случаи соотношения импедансов прилегающих сред, от которых зависят значения, принимаемые выведенными коэффициентами:
1. абсолютно «мягкая» граница 
(вода – воздух):
(3.23)
2. абсолютно «жесткая» граница 
:
(3.24)
Выводы:
1.Отражающие свойства границы (проницаемость) зависят от различия импедансов «прилегающих» сред. При равенстве импедансов отражение отсутствует, и падающая волна полностью проникает во вторую среду.
2.Равенство импедансов предполагает именно равенство произведений плотностей сред на значения скоростей, а не равенство этих значений по отдельности.
3. Коэффициенты отражения и прохождения для разных физических величин могут для одинаковых сочетаний сред принимать разные значения.
4. Коэффициенты отражения и прохождения для разных физических величин не зависят от частоты.
Рассмотренные частные случаи фактически определяют различия между двумя предельными состояниями «граничных» условий, широко используемых в «краевых» задачах математической физики:
Первое условие Дирихле, иначе называемое условием на абсолютно «мягкой» или «свободной» границе:
(3.25)
Второе условие Неймана, иначе называемое условием на абсолютно «жесткой» границе:
(3.26)
Практические следствия, формулируемые на основании обнаруженных закономерностей, означают, прежде всего, необходимость решения задачи согласования импедансов, выполняемую при построении большого числа объектов живой и неживой природы. Кроме того, при решении так называемых обратных задач, когда пытаются восстанавливать профиль (соотношение импедансов) исследуемых сред по результатам ультразвуковых измерений, нужно согласовывать число независимых измерений с количеством восстанавливаемых параметров. Ясно, что по результатам измерений отраженного и прошедшего сигналов можно восстановить два значения импедансов. При этом для конкретизации значения скорости или плотности, обязательно нужны дополнительные измерения. Получение последних встречает затруднения, так как коэффициенты отражения и прохождения по отношению к плоской границе не зависят от частоты.