Определение объема выборки является одной из серьезнейших проблем выборочного аудита. Вкратце ситуацию можно обрисовать так: чтобы вычислить количество элементов, отбор которых обеспечил бы репрезентативность выборки, необходимо иметь представление о содержащихся в генеральной совокупности ошибках, однако до исследования аудитор может лишь предполагать их наличие (или отсутствие) и размер. Получается замкнутый круг.
В российском правиле (стандарте) говорится, что при определении объема (размера) выборки аудиторская организация должна установить риск выборки, допустимую и ожидаемую ошибки. Большинство используемых в мировой практике методов расчета объема выборки строятся именно на этих трех показателях.
Понятия риска выборки (риск первого и второго рода) и допустимой ошибки были рассмотрены ранее, в разделе 1.1.
Ожидаемая ошибка - это ошибка, которую, по мнению аудитора, содержит генеральная совокупность. Определение ожидаемой ошибки - задача не из легких (особенно в российских условиях), а ведь именно от этого показателя во многом зависит объем выборки. При определении ожидаемой ошибки аудитор должен исходить из результатов проверки системы внутреннего контроля, собственной интуиции, а также брать во внимание результаты прошлых проверок данного экономического субъекта, если такие проводились.
Рассмотрим два наиболее распространенных способа определения объем выборки: с помощью специальных таблиц и путем математических расчетов. Расчет объема выборки по таблицам. Описанный ниже способ взят из книги по аудиту известного американского ученого и практика Роберта Монтгомери (1872-1953). Чтобы найти объем выборки аудитор должен определить три указанных выше критерия: надежность (1 - риск выборки), ожидаемая степень отклонений (в % от всей генеральной совокупности) и допустимая степень отклонения (также в % от генеральной совокупности). После этого достаточно воспользоваться специальной таблицей, составленной для соответствующего уровня надежности. Таблица расчета объема выборки для надежности 95% имеет вид:
Таблица: Определение объема выборки (для надежности 95%)
| Ожидаемая степень отклонения, % | Допустимая степень отклонения, % | |||||||||||
| 0,00 | ||||||||||||
| 0,50 | * | |||||||||||
| 1,0 | * | * | ||||||||||
| 2,0 | * | * | * | |||||||||
| 3,0 | * | * | * | * | ||||||||
| 4,0 | * | * | * | * | * | |||||||
| 5,0 | * | * | * | * | * | * | ||||||
| 6,0 | * | * | * | * | * | * | * | * | ||||
| 7,0 | * | * | * | * | * | * | * | * | * | |||
| 8,0 | * | * | * | * | * | * | * | * | * | * |
* Выборка слишком велика, чтобы быть экономичной для большей части аудиторских целей
Например, аудитор установил допустимую ошибку (допустимую степень отклонения в генеральной совокупности) 6%, а ее ожидаемую величину в 1%. При этом аудитор желает быть на 95% уверен, что реальная ошибка, содержащаяся в генеральной совокупности, не превысит установленную им допустимую ошибку. Объем выборки будет определен на пересечении соответствующих граф таблицы, составленной для надежности в 95% - 80 элементов.
Как видно, объем генеральной совокупности игнорируется при определении объема выборки.
Это может показаться странным, но в теории статистики доказано, что для большей части типов совокупностей сам их объем несущественен при определении объема выборки. Представительность же гарантируется процессом случайного отбора. Когда получена выборка с хорошим представительством единиц, добавочные единицы не требуются. Таблицы, вроде приведенной выше, основаны на бесконечных объемах генеральных совокупностей.
Однако при желании можно скорректировать объем выборки на объем генеральной совокупности, воспользовавшись формулой:
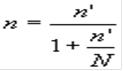
где n' - объем выборки до учета влияния объема генеральной совокупности;- объем генеральной совокупности;- пересмотренный объем выборки после учета влияния объема генеральной совокупности.
По формуле можно видно, что данный фактор позволяет значительно пересмотреть выборку, только когда отбирается более 10% элементов генеральной совокупности.
Нахождение объема выборки путем математических расчетов. Приведенный ниже способ взят из американского стандарта по выборочному аудиту SAS № 39. Данный стандарт разделяет нахождение объема выборки для генеральных совокупностей, в которых не ожидается ошибок или ожидается очень незначительные ошибки, и для совокупностей, которые наверняка содержат отклонения.
В первом случае объем выборки находят умножением фактора уверенности (надежности) (ФУ) на "книжную" стоимость совокупности (В) и делением на допустимую сумму искажения (ДСИ), или
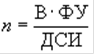
Фактор уверенности берется из таблицы:
| Уровень уверенности (%) | 80,0 | 90,0 | 95,0 | 97,5 | 99,0 | 99,5 |
| Риск (%) (1 - уровень уверенности) | 20,0 | 10, 0 | 5,0 | 2,5 | 1,0 | 0,5 |
| Фактор уверенности (ФУ) | 1,61 | 2,31 | 3,0 | 3,69 | 4,61 | 5,30 |
Предположим, что генеральная совокупность имеет "книжную" стоимость 3 530 000 рублей. Аудитор хочет быть на 80% уверен, что обнаружит искажения в генеральной совокупности, если они превышают 70 000 рублей. Объем выборки составит:
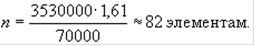
Если не ожидается, что совокупность будет почти свободна от ошибок, то объем часто будет слишком незначительным, чтобы аудитор мог сделать вывод о том, что отклонение в совокупности ниже допустимого уровня. При расчете объема выборки из совокупностей, в которых предположительно содержатся ошибки, используют несколько другой подход. В дополнение к вышеупомянутым факторам аудитор рассматривает ожидаемую сумму искажения (ОСИ) и применяет следующую формулу:
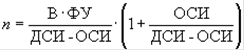
Фактор уверенности определяется по таблице, приведенной выше. Однако наблюдается тенденция несколько занижать объем выборки для уровней уверенности 97,5% и выше. Это может быть исправлено путем использования следующих факторов:
| Уровень уверенности | Фактор уверенности (ФУ) |
| 97,5 | 3,84 |
| 99,0 | 5,43 |
| 99,5 | 6,63 |
Предположим, в предыдущем примере аудитор ожидает, что искажение в совокупности достигнет 20 000 рублей. Тогда объем выборки составит:
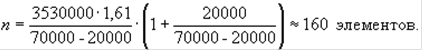
Данная формула применима лишь в случаях, когда ОСИ меньше, чем ДСИ (т. е. ожидаемая ошибка меньше допустимой). На практике аудитор должен рассматривать возможность применения этой формулы только тогда, когда ОСИ не больше, чем ДСИ/2.
Реально существует больше способов определения объема выборки, которые по сути схожи с рассмотренными. Однако на примере приведенных способов видно, что аудитор может получить лишь весьма близкий к истине результат. В связи с этим часто аудиторы вообще не рассчитывают специальным образом объем выборки, а берут его на свое усмотрение с учетом влияния следующих факторов:
| Фактор | Влияние на объем выборки |
| Доверие к системе внутреннего контроля клиента | Выше доверие - меньше выборка. |
| Величина определенной аудитором допустимой ошибки | Меньше допустимая ошибка - больше выборка |
| Ожидаемый размер ошибки | Меньше ожидаемая ошибка - меньше выборка |
| Необходимая степень уверенности (надежности) | Выше необходимая уверенность - больше выборка |
| Применение группировки (стратификация) | Применяется стратификация - уменьшается выборка |
| Число единиц генеральной совокупности | Больше генеральная совокупность - больше выборка (несущественный при больших объемах генеральной совокупности фактор) |
Особенно важным фактором из перечисленных, с помощью которого можно влиять на объем выборки, является стратификация. Правильная стратификация (разделение генеральной совокупности по какому-либо признаку) позволяет не только вычленить из совокупности наиболее важные элементы для их сплошной проверки, но и обеспечивает большую однородность элементов внутри полученных групп, что и позволяет снизить объем выборки.
Определяя объем выборки на собственное усмотрение, аудитор отступает от предписанных правил, хотя такой подход тоже допустим (это особенное актуально в российской практике аудита, когда невозможно даже примерно предположить какая ошибка содержится в совокупности). Главное при этом следить, чтобы взятое число не оказалось слишком мало применительно к конкретному случаю.
На этапе определения объема выборки его еще называют начальным объем, потому что по результатам проверки выбранных элементов аудитор может пересмотреть начальный объем выборки и провести дополнительное исследование.
Оценка результатов
Поскольку целью выборки является получение выводов по всей генеральной совокупности, аудитор старается сформировать репрезентативную (представительную) совокупность путем отбора элементов выборки, обладающих характеристиками, типичными для генеральной совокупности. Проверяемая совокупность элементов должна формироваться таким образом, чтобы исключалась предвзятость. Такими свойствами обладает статистическая выборка.
Оценка результатов проведенной проверки с применением статистических методов всей совокупности (экстраполяция) проводится по следующей формуле (так называемая прогнозируемая ошибка):
Сумма нарушений
Прогнозируемая ошибка = ------------------- х Сумма совокупности
Сумма проверенных элементов
Практическая часть
Пример 1
Проверяется совокупность документов, нумерация которых начинается с № 300 и заканчивается № 2500. Необходимо отобрать 10 документов. Необходимым условием является, чтобы проверяемые документы были пронумерованы подряд, и не обязательно начиная с единицы.
Вариант 1. Используем таблицу случайных чисел от 0 до 1 (табл. 1). Выбираем первую цифру, например, 0,0441 (первый столбец, вторая строка). Для получения остальных чисел берем подряд вниз по колонке еще 9 чисел.
Как видим, эти числа не соответствуют номерам совокупности. Нам нужны случайные числа в границах от 300 до 2500. Чтобы привести случайные числа в соответствие с номерами совокупности, умножаем случайное число из таблицы на разность 2500 (конечное значение) и 300 (начальное значение), то есть на 2200. Затем к полученному результату прибавляем начальное значение 300.
Возьмем первое случайное число 0,0441.
,0441×2200 + 300 = 397.
Таким же образом поступаем с остальными девятью числами. Получаем номера документов, составляющих выборку (табл. 2).
Таблица 1. Выборка документов
| Случайное число | Номер документа |
| 0,0441 | |
| 0,2017 | |
| 0,1797 | |
| 0,7575 | |
| 0,9374 | |
| 0,3228 | |
| 0,0366 | |
| 0,8230 | |
| 0,9885 | |
| 0,6219 |
Вариант 2. Для формирования выборки применяем генератор случайных чисел в Excel. В первую ячейку вводим функцию «=случмежду(300;2500)» и методом «протяжки» получаем 10 случайных чисел. Допустим, получены числа 1365, 903, 1371, 996, 957, 1435, 2285, 711, 394 и 1337. Это и есть номера документов, которые нужно проверить. Не следует забывать фиксировать полученные значения.
Пример 2
Имеем для проверки совокупность с № 300 до № 2500, то есть 2200 документов. Проверке подлежат 100 документов. Делим 2200 на 100 и получаем число 22. Это интервал выборки, который указывает, что проверке подлежит каждый 22-й документ.
После этого случайным образом выбираем номер первого документа для проверки, например с применением таблицы случайных чисел. Допустим, этот номер будет 20. Затем к этому числу прибавляем число 22, получаем следующий номер для проверки 42, к этому номеру опять прибавляем 22 и получаем следующий номер 64 и т.д. Номера для проверки 20, 42, 64, 86, 108 и т.д., пока не будут отобраны все 100 документов.
Может оказаться, что для отбора всех документов не хватит номеров в отбираемой совокупности. В этом случае продолжение счета переходит в начальные номера до тех пор, пока не будут отобраны все запланированные 100 документов.
Пример 3
При нестатистической выборке аудитор для отбора элементов опирается на профессиональное суждение.
Пусть для некоторой проверяемой совокупности суммарная стоимость всех элементов составляет 64 000 000 руб., уровень существенности - 3 000 000 руб.
Допустим, что в ходе проверки были рассмотрены элементы репрезентативной (то есть с применением статистического метода) выборки на общую сумму 595 000 руб., а сумма обнаруженных ошибок составляет 17 000 руб.
В этом случае получаем:
000 руб.: 595 000 руб. х 64 000 000 руб. = 1 828 571 руб.
Полученную прогнозируемую ошибку сравниваем с установленным уровнем существенности. Она значительно меньше установленного уровня существенности (3 000 000 руб.). Следовательно, проверяемая совокупность достоверна.