Экспериментально-аналитические методы исследований

Физические процессы можно исследовать аналитическими или экспериментальными методами.

Аналитические методы позволяют изучать процессы на основе математических моделей, которые могут быть представлены в виде функций, уравнений, систем уравнений, в основном дифференциальных или интегральных. Обычно в начале создают грубую модель, которую затем, после ее исследования, уточняют. Такая модель позволяет достаточно полно изучать физическую сущность явления.

Однако им свойственны существенные недостатки. Для того чтобы из всего класса найти частное решение, присущее лишь данному процессу, необходимо задать условия однозначности. Часто неправильное принятие краевых условий приводит к искажению физической сущности явления, а отыскать аналитическое выражение, наиболее реально отображающие это явление, или вообще невозможно или чрезвычайно затруднительно.

Экспериментальные методы позволяют глубоко изучить процессы в пределах точности техники эксперимента, особенно те параметры, которые представляют наибольший интерес. Однако результаты конкретного эксперимента не могут быть распространены на другой процесс, даже весьма близкий по своей сути. Кроме того, из опыта трудно установить, какие из параметров оказывают решающее влияние на ход процесса, и как будет протекать процесс, если меняются одновременно различные параметры. Экспериментальные методы позволяют установить лишь частные зависимости между отдельными переменными в строго определенных интервалах. Использование этих зависимостей за пределами этих интервалов может привести к грубым ошибкам.

Таким образом, и аналитические, и экспериментальные методы имеют свои преимущества и недостатки. Поэтому чрезвычайно плодотворным являются сочетание положительных сторон этих методов исследований. На этом принципе основаны методы сочетания аналитических и экспериментальных исследований, которые, в свою очередь, основываются на методах аналогии, подобия и размерностей.

Метод аналогии. Метод аналогии применяют, когда разные физические явления описываются одинаковыми дифференциальными уравнениями.

Рассмотрим суть метода аналогии на примере. Тепловой поток зависит от температурного перепада (закон Фурье):

, (4.22)

где λ – коэффициент теплопроводности.

Массперенос или перенос вещества (газа, пара, влаги, пыли) определяется перепадом концентрации вещества С (закон Фика):

(4.23)

– коэффициент масспереноса.

Перенос электричества по проводнику с погонным сопротивлением обусловливается перепадом напряжения (закон Ома):

(4.24)

где ρ – коэффициент электропроводности.

Три различных физических явления имеют идентичные математические выражения. Таким образом, их можно исследовать методом аналогии. При этом в зависимости от того, что принимается за оригинал и модель, могут быть различные виды моделирования. Так, если тепловой поток q _т изучают на модели с движением жидкости, то моделирование называют гидравлическим; если его исследуют на электрической модели, моделирование называют электрическим.

Идентичность математических выражений не означает, что процессы абсолютно аналогичны. Чтобы на модели изучать процесс оригинала, необходимо соблюдать критерии аналогии. На прямую сравнивать q _т и q _э, коэффициенты теплопроводности λ и электропроводности ρ, температуру Т и напряжения U нет смысла. Для устранения этой несопоставимости оба уравнения необходимо представить в безразмерных величинах. Каждую переменную П следует представить в виде произведения постоянной размерности П _п на переменную безразмерную П _б:

П = П _п ∙ П _б. (4.25)

Имея в виду (4.25), запишем выражения для q _т и q _э в следующем виде:

Подставим в уравнения (4.22) и (4.24) значения преобразованных переменных, в результате чего получим:

;

Оба уравнения написаны в безразмерном виде и их можно сравнивать. Уравнения будут идентичны, если

(4.26)

Это равенство называют критерием аналогии. С помощью критериев устанавливают параметры модели по исходному уравнению объекта.

В настоящее время широко применяется электрическое моделирование. С его помощью можно изучить различные физические процессы (колебания, фильтрацию, массперенос, теплопередачу, распределение напряжений). Это моделирование универсально, простое в эксплуатации, не требует громоздкого оборудования. При электрическом моделировании применяют аналоговые вычислительные машины (АВМ). Под которыми, как мы уже говорили, понимают определенное сочетание различных электрических элементов, в которых протекают процессы, описываемые математическими зависимостями, аналогичными с зависимостями для изучаемого объекта (оригинала). Существенным недостатком АВМ является сравнительно небольшая точность и не универсальность, так как для каждой задачи необходимо иметь свою схему, а значить и другую машину.

Для решения задач используют и другие методы электрического моделирования: метод сплошных сред, электрических сеток, электромеханическая аналогия, электрогидродинамическая аналогия и др. Плоские задачи моделируют с использованием электропроводной бумаги, объемные – электролитических ванн.

Метод размерностей. В ряде случаев встречаются процессы, которые не могут быть непосредственно описаны дифференциальными уравнениями. Зависимость между переменными величинами в таких случаях можно установить экспериментально. Для того чтобы ограничить эксперимент и отыскать связь между основными характеристиками процесса, эффективно применять метод анализа размерностей.

Анализ размерностей является методом установления зависимости между физическими параметрами изучаемого явления. Основан он на изучении размерностей этих величин.

Измерение физической характеристики Q означает ее сравнение с другим параметром q той же самой природы, то есть нужно определить во сколько раз Q больше чем q. В этом случае q является единицей измерения.

Единицы измерения составляют систему единиц, например, Международную систему СИ. Система включает единицы измерения, которые независимы одна от другой, их называют основными или первичными единицами. В системе СИ таковыми являются: масса (килограмм), длина (метр), время (секунда), сила тока (ампер), температура (градус Кельвина), сила света (кандела).

Единицы измерений других величин называются производными или вторичными. Они выражаются с помощью основных единиц. Формула, которая устанавливает соотношение между основными и производными единицами называется размерностью. Например, размерность скорости V является

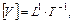(4.27)

где L – условное обозначение длины, а Т – времени.

Эти символы представляют собой независимые единицы системы единиц измерения (Т измеряется в секундах, минутах, часах и т.д., L в метрах, сантиметрах, и т.д.). Размерность выводится с помощью уравнения, которое в случае скорости имеет следующий вид:

,

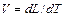откуда вытекает формула размерности для скорости. Анализ размерностей базируется на следующем правиле: размерность физической величины является произведением основных единиц измерения, возведенных в соответствующую степень.

В механике используют, как правило, три основные единицы измерения: массу, длину и время. Таким образом, в соответствии с вышеприведенным правилом, можно записать:

(4.28)

где N – обозначение производной единицы измерения;

L, M, T – обозначения основных (длина, масса, время) единиц;

l, m, t – неизвестные показатели, которые могут быть представлены целыми или дробными числами, положительными или отрицательными.

Существуют величины, размерность которых состоит из основных единиц в степени, равной нулю. Это так называемые безразмерные величины. Например, коэффициент разрыхления породы представляет собой отношение двух объемов, откуда

следовательно, коэффициент разрыхления есть безразмерная величина.

Если в ходе эксперимента установлено, что определяемая величина может зависеть от нескольких других величин, то в этом случае возможно составить уравнение размерностей, в котором символ изучаемой величины располагается в левой части, а произведение других величин – в правой. Символы в правой части имеют свои неизвестные показатели степени. Чтобы получить окончательно соотношение между физическими величинами, необходимо определить соответствующие показатели степени.

Например, необходимо определить время t, затраченное телом, имеющим массу m, при прямолинейном движении на пути l под действием постоянной силы f. Следовательно, время зависит от длины, массы и силы. В этом случае уравнение размерностей запишется следующим образом:

.

Левая часть уравнения может быть представлена в виде . Если физические величины изучаемого явления выбраны правильно, то размерности в левой и правой частях уравнения должны быть равны. Тогда система уравнений показателей степени запишется:

тогда x = y =1/2 и z = –1/2.

Это значит, что время зависит от пути как , от массы как и от силы как . Однако получить окончательное решение поставленной задачи с помощью анализа размерностей невозможно. Можно установить лишь общую форму зависимости:

, (4.29)

где k – безразмерный коэффициент пропорциональности, который определяют путем эксперимента.

Таким способом находят вид формулы и условия эксперимента. Необходимо определить лишь зависимость между двумя величинам: и А, где А = .

Если размерности левой и правой частей уравнения равны, это значит, что рассматриваемая формула аналитическая и расчеты могут выполняться в любой системе единиц. Напротив, если используется эмпирическая формула, необходимо знать размерности всех членов этой формулы.

Используя анализ размерностей, можно ответить на вопрос: не потеряли ли мы основные параметры, влияющие на данный процесс? Иначе говоря, найденное уравнение является полным или нет?

Предположим, что в предыдущем примере тело при движении нагревается и поэтому время зависит также от температуры С.

Тогда уравнение размерностей запишется:

.

Откуда легко найти, что 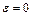, т.е. изучаемый процесс не зависит от температуры и уравнение (4.29) является полным. Наше предположение не верно.

Таким образом, анализ размерностей позволяет:

– найти безразмерные соотношения (критерии подобия), чтобы облегчить экспериментальные исследования;

– выбрать влияющие на изучаемое явление параметры, чтобы найти аналитическое решение задачи;

– проверить правильность аналитических формул.

Метод анализа размерностей очень часто применяется в исследованиях и в более сложных случаях, чем рассмотренный пример. Он позволяет получить функциональные зависимости в критериальном виде. Пусть известна в общем виде функция F для какого-либо сложного процесса

(4.30)

содержащая k неизвестных постоянных или переменных размерных величин. Необходимо отыскать F и найти ее зависимость от переменных.

Значения имеют определенную размерность единиц измерения. Метод размерностей предусматривает выбор из числа k трех основных независимых друг от друга единиц измерения. Остальные (k –3) величины, входящие в функциональную зависимость (4.30), выбирают так, чтобы они были представлены в функции F как безразмерные, т.е. в критериях подобия. Преобразования производят с помощью основных, выбранных единиц измерения. При этом функция (4.30) принимает вид:

.

Три единицы означают, что первые три числа являются отношением n ₁, n ₂ и n ₃ к соответственно равным значениям а, в, с. Выражение (4.30) анализируют по размерностям величин. В результате устанавливают численные значения показателей степени х … х ₃, у … у ₃, z … z ₃ и определяют критерии подобия.

Наглядным примером использования метода анализа размерностей при разработке аналитико-эскпериментальных методов является расчетный метод Ю.З. Заславского, позволяющий определить параметры крепи одиночной выработки.

ЛЕКЦИЯ 8

Теория подобия. Теория подобия – это учение о подобии физических явлений. Ее использование наиболее эффективно в том случае, когда на основе решения дифференциальных уравнений зависимости между переменными отыскать невозможно. В этом случае, воспользовавшись данными предварительного эксперимента, с применением метода подобия составляют уравнение, решение которого можно распространить за пределы эксперимента. Этот метод теоретического исследования явлений и процессов возможен лишь на основе комбинирования с экспериментальными данными.

Теория подобия устанавливает критерии подобия различных физических явлений и с помощью этих критериев исследует свойства явлений. Критерии подобия представляют собой безразмерные отношения размерных физических величин, определяющих изучаемые явления.

Использование теории подобия дает важные практические результаты. С помощью этой теории осуществляют предварительный теоретический анализ проблемы и выбирают систему величин, характеризующих явления и процессы. Она является основой для планирования экспериментов и обработки результатов исследований. Совместно с физическими законами, дифференциальными уравнениями и экспериментом, теория подобия позволяет получать количественные характеристики изучаемого явления.

Формулирование проблемы и установление плана эксперимента на базе теории подобия значительно упрощается благодаря функциональной зависимости между совокупностью величин, определяющих явление или поведение системы. Как правило, в этом случае речь не идет о том, чтобы изучать отдельно влияние каждого параметра на явление. Очень важно, что можно достичь результатов с помощью одного лишь эксперимента над подобными системами.

Свойства подобных явлений и критерии подобия изучаемых явлений характеризуются тремя теоремами подобия.

Первая теорема подобия. Первая теорема, установленная Ж. Бертраном в 1848г., базируется на общем понятии динамического подобия Ньютона и его втором законе механики. Эта теорема формулируется следующим образом: для подобных явлений можно найти определенную совокупность параметров, называемых критериями подобия, которые равны между собой.

Рассмотрим пример. Пусть два тела, имеющие массы m ₁ и m ₂, перемещаются с ускорениями соответственно а ₁ и а ₂ под действием сил f ₁и f ₂. Уравнения движения имеют вид:

или ,

или

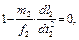
или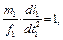

Распространяя результат для n подобных систем, получим критерий подобия:

(4.31)

Критерий подобия условились обозначать символом П, тогда результат вышеприведенного примера запишется:

(4.32)

Таким образом, в подобных явлениях соотношение параметров (критерии подобия) равны между собой и для этих явлений справедливо 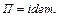Обратное утверждение также имеет смысл. Если критерии подобия равны, то явления являются подобными.

Найденное уравнение (4.32) называется критерием динамического подобия Ньютона, оно аналогично выражению (4.29), полученному с помощью метода анализа размерностей, и является частным случаем критерия термодинамического подобия, основанного на законе сохранения энергии.

При исследовании сложного явления могут развиваться несколько различных процессов. Подобие каждого из этих процессов обеспечивается подобием явления в целом. С точки зрения практики очень важно, что критерии подобия могут трансформироваться в критерии другого вида с помощью деления или умножения на константу k. Например, если имеются два критерия П ₁ и П ₂, следующие выражения являются справедливыми:

(4.33)

Если подобные явления рассматриваются во времени и в пространстве, речь идет о критерии полного подобия. В этом случае описание процесса наиболее сложно, оно позволяет иметь не только численное значение параметра (силу удара взрывной волны в точке, удаленной от места взрыва на 100 м), но также развитие, изменение рассматриваемого параметра во времени (например, увеличение силы удара, скорость затухания процесса и т.д.).

Если подобные явления рассматриваются только в пространстве или во времени, они характеризуются критериями неполного подобия.

Наиболее часто, используют приблизительное подобие, при котором не рассматриваются параметры, влияющие на данный процесс в незначительной степени. Вследствие этого и результаты исследований будут приблизительными. Степень этого приближения определяется путем сравнения с практическими результатами. Речь идет в этом случае о критериях приблизительного подобия.

Вторая теорема подобия (П – теорема). Она была сформулирована в начале XX века учеными А. Федерманом и У. Букингемом следующим образом: каждое полное уравнение физического процесса может быть представлено в форме (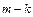) критериев (безразмерных зависимостей), где m есть число параметров, а k – число независимых единиц измерения.

Такое уравнение может быть решено по отношению к любому критерию и может быть представлено в виде критериального уравнения:

. (4.34)

Благодаря П- теореме возможно уменьшить число переменных размерных величин до (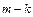) безразмерных величин, что упрощает анализданных, планирование эксперимента и обработку его результатов.

Обычно, в механике, в качестве основных единиц принимаются три величины: длину, время и массу. Тогда при исследовании явления, которое характеризуется пятью параметрами (включая, безразмерную константу), достаточно получить взаимосвязь между двумя критериями.

Рассмотрим пример приведения величин к безразмерному виду, используемый обычно в механике подземных сооружений. Напряженное деформированное состояние пород вокруг выработки предопределяется весом вышележащей толщи γН, где γ – объемный вес пород, Н – глубина расположения выработки от поверхности; прочностной характеристикой пород R; сопротивлением крепи q; смещениями контура выработки U; размерами выработки r; модулем деформации Е.

В общем виде зависимость можно записать следующим образом:

В соответствии с П- теоремой система из п параметров и одной определяемой величины должна дать безразмерных комбинаций. В нашем случае время не принимается во внимание, следовательно, получаем четыре безразмерные комбинации.

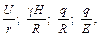
из которых можно составить более простую зависимость:

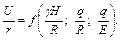
Третья теорема подобия. Эта теорема сформулирована акад. В.Л. Кирпичевым в 1930 г. следующим образом: необходимым и достаточным условием подобия является пропорциональность схожих параметров, составляющих часть условия однозначности, и равенство критериев подобия изучаемого явления.

Два физических явления подобны, если они описываются одной и той же системой дифференциальных уравнения и имеют подобные (граничные) условия однозначности, а их определяющие критерии подобия – численно равны.

Условиями однозначности являются условия, с помощью которых конкретное явление отличают от всей совокупности явлений того же типа. Подобие условий однозначности устанавливается в соответствии со следующими критериями:

– подобие геометрических параметров систем;

– пропорциональность физических постоянных, имеющих основное значение для изучаемого процесса;

– подобие начальных условий систем;

– подобие граничных условий систем в течение всего рассматриваемого периода;

– равенство критериев, имеющих основное значение для изучаемого процесса.

Подобие двух систем будет обеспечено в случае пропорциональности их схожих параметров и равенства критериев подобия, определенных с помощью П- теоремы из полного уравнения процесса.

Различают два типа задач в теории подобия: прямую и обратную. Прямая задача состоит в определении подобия при известных уравнениях. Обратная задача заключается в установлении уравнения, которое описывает подобие схожих явлений. Решение задачи сводится к определению критериев подобия и безразмерных коэффициентов пропорциональности.

Задача нахождения уравнения процесса с помощью П- теоремы решается в следующем порядке:

– определяют тем или иным методом все параметры, влияющие на данный процесс. Один из параметров записывается в виде функции от других параметров:

(4.35)

– предполагают, что уравнение (4.35) является полным и однородным по отношению к размерности;

– выбирают систему единиц измерений. В этой системе выбирают независимые параметры. Число независимых параметров равно k;

– составляют матрицу размерностей выбранных параметров и рассчитывают детерминант этой матрицы. Если параметры независимы, то детерминант не будет равен нулю;

– находят комбинации критериев, используя метод анализа размерностей, их число в общем случае равно k –1;

– определяют коэффициенты пропорциональности между критериями с помощью эксперимента.

Критерии механического подобия. В горной науке наибольшее применение находят критерии механического подобия. При этом считают, что другие физические явления (термические, электрические, магнитные и др.) не влияют на изучаемый процесс. Чтобы получить необходимые критерии и постоянные подобия используют закон динамического подобия Ньютона и метод анализа размерностей.

В качестве основных единиц принимаются длина, масса и время. Все остальные характеристики рассматриваемого процесса будут находиться в зависимости от этих трех основных единиц. Следовательно, механическое подобие устанавливает критерии для длины (подобие геометрическое), времени (подобие кинематическое) и массы (подобие динамическое).

Геометрическое подобие двух подобных систем будет иметь место, если все размеры модели изменены в С_l раз по отношению к системе, имеющей реальные размеры. Иначе говоря, отношение расстояний в натуре и на модели между любой парой аналогичных точек есть величина постоянная, называемая геометрическим масштабом:

. (4.36)

Отношение площадей подобных фигур равно квадрату коэффициента пропорциональности 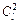, отношение объемов – .

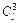Условие кинематического подобия будет иметь место, если аналогичные частицы систем, перемещаясь по геометрически подобным траекториям, проходят геометрически подобные расстояния за отрезки времени t _n в натуре и t _m на модели, которые отличаются коэффициентом пропорциональности:

(4.37)

Условие динамического подобия будет иметь место, если, кроме условий (4.36) и (4.37), еще и массы аналогичных частиц подобных систем отличаются одна от другой коэффициентом пропорциональности:

. (4.38)

Коэффициенты C_l, C_t, и C_m названы коэффициентами подобия.

Имея динамическое подобие, очень легко установить зависимости между всеми характеристиками любой механической системы. В самом деле:

– для скоростей (4.39)

– для ускорений (4.40)

– для сил (4.41)

– для мощности . (4.42)

Следовательно, коэффициенты подобия различных величин могут быть выражены через коэффициенты динамического подобия С_l, C_t и C_m.

Иногда удобно выражать коэффициенты подобия, используя вторичные единицы измерения. Например, масса в условии (4.38) может быть представлена в виде произведения объема на плотность. Тогда,

Так как условие геометрического подобия нами уже определено, то условие динамического подобия может быть дано отношением плотностей подобных систем

(4.43)

Представляя в выражении (4.41) массы частиц в виде плотности и объема, получим:

(4.44)

Зависимости (4.44) представляют собой различные формы математической записи одного и того же закона динамического подобия.

Заменим в (4.41) коэффициенты пропорциональности соответствующими отношениями:

. (4.45)

В задачах механики горных пород выражение динамического подобия преобразуется, учитывая гравитационные силы и напряжения в породном массиве , и принимает следующую форму:

(4.46)

Анализ критерия (4.46) показывает, что в случае геометрического масштаба моделирования , чтобы обеспечить механическое подобие модели и натуры, возможны три условия:

и ; и ; и .

Первое условие соответствует наиболее простой механической модели, которая воспроизводит явление, соблюдая геометрическое подобие и сохраняя его физическую природу. Моделируемые явления количественно протекают в этом случае иначе, а геометрические размеры и силы изменяются пропорционально

Если соблюдают условие и , то необходимо выбрать материал модели по формуле: т.е. объемный вес модели должен быть выше объемного веса породы в раз. Это условие обеспечивается, если в качестве материала модели использовать натуральную породу, а объемный вес модели увеличить с помощью сил инерции, например, вращением в центрифуге.

Если для создания модели используют искусственный материал, механические характеристики которого меньше, чем аналогичные параметры в натуре, механическое подобие будет обеспечено при условии:

(4.47)

Эти материалы называются эквивалентными.

Выбор условий подобия в механике горных пород зависит также от уровня развития процессов деформации пород. При деформируемости массивов в пределах упругости должны соблюдаться два условия

и . (4.48)

В случае упругих и пластических 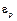деформаций:

, где . (4.49)

При моделировании процессов разрушения пород условия подобия зависят от типа разрушения:

– от сжатия

– от растяжения (4.50)

– от сдвига .

При использовании теории подобия удобно оперировать критериями подобия, которые обозначаются двумя латинскими буквами фамилии ученых. Рассмотрим некоторые критерии подобия.

Подобие механических систем динамического характера выражают критерием Ньютона:

.

Изучая потоки жидкостей, применяют критерий Рейнольда, который является показателем отношения сил инерции к силам трения:

где u – динамическая вязкость.

Критерий Эйлера Eu характеризует соотношения давления и сил инерции:

,

где – падение давления при движении жидкости в трубопроводе вследствие трения.

Подобие сил тяжести характеризует критерий Фруда:

Временное подобие характеризует критерий гомохронности:

.

Критерий Фурье характеризует скорость выравнивания тепла в теле:

где a – коэффициент температуропроводности.

Все приведенные, а также и другие критерии, являются безразмерными и независимыми друг от друга, поэтому их сочетание дает новые критерии. Использовать критерии подобия при исследовании явлений и процессов очень удобно. Для этого экспериментальные данные обрабатывают в критеральном виде, т.е. в дифференциальные уравнения вместо переменных l, a, t и т.д. ставят безразмерные критерии подобия. Затем приступают к решению теоретического уравнения в критериальном виде. Полученное аналитическое решение позволяет распространить результаты единичного опыта на группу подобных явлений и анализировать переменные величины за пределами эксперимента.

Критерии подобия применяются и для решения дифференциальных уравнений со многими переменными. В этом случае уравнения и граничные условия целесообразно представлять в критериальном безразмерном виде, хотя это иногда и нелегко. Решение уравнений в безразмерном виде менее трудоемко, поскольку число переменных уменьшается, анализ аналитических выражений упрощается, а объем расчетов существенно снижается.

ЛЕКЦИЯ 9