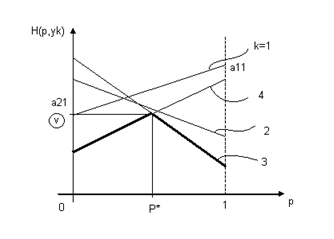
Пусть имеется некоторая матричная игра Г=<X,Y,H> (где X и Y — множества стратегий 1го и 2го игроков соответственно, а Н — платежная матрица),  H=(aij)
H=(aij) 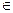 Rm*n
Rm*n
Требуется найти оптимальную смешанную стратегию, т.е.
p*=(p1*,p2*,…,pm*) и q*=(q1*,q2*,…,qn*), при которых
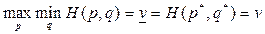
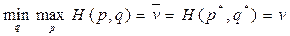 ,
,
где v — цена игры.
Для решения этой задачи можно применять линейное программирование.
Будем считать, что все aij 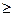 0, игра Г’ эквивалентна игре Г, H’=H+L, L — число, при котором неравенство будет выполняться (при переходе от игры Г к игре Г’).
0, игра Г’ эквивалентна игре Г, H’=H+L, L — число, при котором неравенство будет выполняться (при переходе от игры Г к игре Г’).
Далее предположим, что 2й игрок принимает стратегию yk, 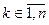 , тогда выигрыш игрока 1 будет определяться условием
, тогда выигрыш игрока 1 будет определяться условием
p1a1k + p2a2k + … + pmamk 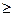 v,
v, 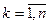 (*)
(*)
(равенство v достигается, если k-я стратегия является рабочей)
pi 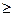 0,
0, 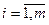 ;
;  pi aik > 0
pi aik > 0 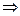 v>0 (т.к. левая часть неравенства (*) больше нуля).
v>0 (т.к. левая часть неравенства (*) больше нуля).
Разделим неравенство (*) на v:
t1a1k + t2a2k +…+ tmamk 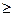 1, где ti=
1, где ti= 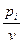 , ti
, ti 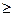 0,
0, 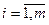
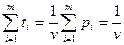
Цель стратегии 1-го игрока — максимизировать выигрыш:
v 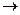 max
max 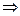

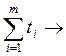 min
min
Исходя из рассмотренных условий, задачу линейного программирования можно сформулировать так:
1) ti 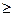 0,
0, 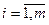
2) 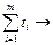 min
min
3) 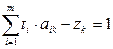 , причем zk=0 для рабочих стратегий, zk>0 для нерабочих стратегий.
, причем zk=0 для рабочих стратегий, zk>0 для нерабочих стратегий.
Решение этой задачи позволяет:
1. Вычислить ti*.
2. Определить те k, при которых zk=0 (т.е. найти рабочие стратегии 2го игрока)
3. 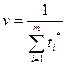
4. pi*=ti* v
Для определения стратегии 2го игрока можно поступить двояко:
1) сформулировать двойственную задачу
2) использовать информацию о полезных стратегиях 2-го игрока (полезные стратегии – при zk=0)
Пусть найдена полезная стратегия игрока yj, 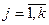 ,
, 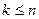 . Для определения оптимальной стратегии qj*,
. Для определения оптимальной стратегии qj*, 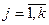 для рабочих стратегий 1-го игрока можно записать условие
для рабочих стратегий 1-го игрока можно записать условие
q1ai1 + q2ai2 + … + qkaik 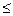 v,
v, 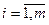
(причем если i-я стратегия 1-го игрока рабочая, то =v,а если нет, то >v)
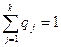 q1ai1 + q2ai2 + … + qkaik
q1ai1 + q2ai2 + … + qkaik 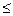 v,
v, 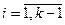
- система уравнений для определения оптимального q.
ПРИМЕР.
Пусть имеется некоторая игра с матрицей A= 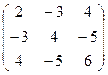
A+5 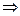 A1=
A1= 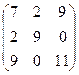
Предположим, что все стратегии рабочие. Составляем систему уравнений:
7t1 + 2t2 + 9t3 - z1 = 1
2t1 + 9t2 - z2 = 1
9t1+11t3 - z3 = 1
Решение этих уравнений при условии t1 + t2 + t3  min:
min:
t1 = 0,05
t2 = 0,1
t3 = 0,05
v(A1) = 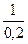 = 5
= 5 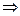 p1=0,05*5=0,25
p1=0,05*5=0,25
p2=0,1*5=0,5
p3=0,05*5=0,25
v(A)=v(A1) - 5=0 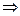 игра справедливая. Найдём стратегию второго игрока:
игра справедливая. Найдём стратегию второго игрока:
q1* + q2* + q3* = 1
2q1 + 9q2 = 5 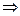 q1=q3=0,25
q1=q3=0,25
9q1 + 11q3 =5 q2=0,5
Графическое решение игр 2*n и m*2
Рассмотрим игру (2*n) с матрицей
 A=
A= 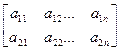
Выигрыш 1-го игрока H(p,yk)=p1a1k + p2a2k = p1a1k + (1-p1)a2k, 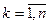
На плоскости такая зависимость изображается отрезком прямой, причем при p=0 H(p,yk)=a2k, p=1 H(p,yk)=a1k
Таким образом, получаем семейство из n прямых:
Исходя из условия гарантированного выигрыша, его величина при разных значениях р будет определяться нижней границей множества этих прямых. Очевидно, что оптимальная стратегия соответствует той точке полученного множества, в которой значение функции максимально, а само это максимальное значение есть значение игры.
Рабочими стратегиями 2-ого игрока являются в данном случае 3я и 4я, а значит, оптимальная стратегия 1-ого игрока определяется из системы уравнений:
q3 + q4 = 1
a23q3 + a24q4 = v
Рассмотрим теперь игру (m*2) с матрицей 
Эту игру удобно рассматривать для второго игрока. Как и в предыдущем случае, строится семейство из m отрезков прямых, отображающих зависимость величины функции выигрыша 2го игрока от выбираемой им стратегии:
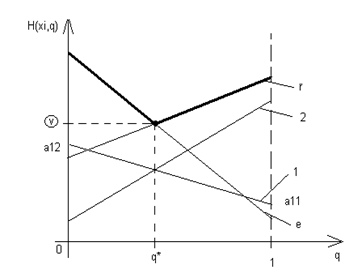
Н(xi,q)= ai1q + ai2(1-q),  ,
, 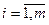
Исходя из разумности поведения 1-ого игрока, проигрыш 2-ого определяется верхней огибающей семейства этих прямых. Значения q* и v находятся как абсцисса и ордината нижней вершины огибающей, а затем оптимальная стратегия 2-ого игрока определяется исходя из его рабочих стратегий (в данном случае рабочими стратегиями 2-ого игрока являются xr и xe), аналогично предыдущему случаю.
Во всех этих случаях число рабочих стратегий обоих игроков одинаково.
Бесконечные антагонистические игры\
Антагонистическая игра называется бесконечной, если хотя бы у одного из двух игроков существует бесконечное множество стратегий.
Рассмотрим общие сведения об этих играх.
Имеется игра Г=<X,Y,H>, X и Y — произвольные множества элементов 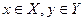 . На каждую ситуацию (x,y) определена функция H=H(x,y), задающая выигрыш 1-ого и проигрыш 2-ого игрока. Обычно считают, что x и y — непрерывно меняющиеся параметры. Функция H(x,y) может быть непрерывной или кусочно-непрерывной.
. На каждую ситуацию (x,y) определена функция H=H(x,y), задающая выигрыш 1-ого и проигрыш 2-ого игрока. Обычно считают, что x и y — непрерывно меняющиеся параметры. Функция H(x,y) может быть непрерывной или кусочно-непрерывной.
В бесконечном варианте принцип разумности в поведении игроков сохраняется: 1-ый игрок стремится увеличить свой выигрыш за счет выбора стратегии x 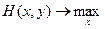 , а 2-ый стремится уменьшить свой проигрыш за счет выбора своей стратегии y
, а 2-ый стремится уменьшить свой проигрыш за счет выбора своей стратегии y 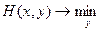 .
.
Как и в конечном варианте игры, величину 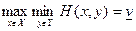 называют нижней ценой игры,
называют нижней ценой игры, 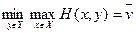 — верхней ценой игры. Если
— верхней ценой игры. Если 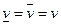 , это бесконечная игра с седловой точкой (седловая точка — точка равновесия).
, это бесконечная игра с седловой точкой (седловая точка — точка равновесия).
Если (x0,y0) — точка равновесия, то H(x,y0) 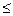 H(x0,y0)
H(x0,y0) 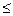 H(x0,y). Любое отклонение от x0 приводит к уменьшению выигрыша 1-ого игрока, а отклонение от y0 — к увеличению проигрыша 2-ого.
H(x0,y). Любое отклонение от x0 приводит к уменьшению выигрыша 1-ого игрока, а отклонение от y0 — к увеличению проигрыша 2-ого.
В геометрии седлообразная точка не зависит от направления, вдоль которого функция возрастает или убывает. В данном случае седловая точка максимальна по x и минимальна по y
Функция H(x,y) должна быть аналитической, т.е. должны существовать ее первые производные по x и по y.
В теории игр нередко максимум и минимум принадлежат границам множеств Х или Y, а не являются внутренней точкой. В общем случае 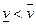 решение нужно искать в смешанном расширении игры.
решение нужно искать в смешанном расширении игры.
Общих методов решения бесконечных антагонистических игр в настоящее время не разработано. В литературе описываются некоторые частные виды таких игр, которые предполагают достаточно простое решение, например, строго выпуклые игры на единичном квадрате.