| Расчетные нагрузки | Расчет лебедок | Расчет якорей | ||||
| верховой ветер | низовой ветер | поперечный ветер | верховой ветер | низовой ветер | поперечный ветер | |
| Ветровая нагрузка расчетной интенсивности WP | - | - | - | + | + | + |
| Ветровая нагрузка при скорости ветра V = 10 м/с | + | + | + | - | - | - |
| Гидродинамическое давление на подводную часть плавучей системы максимальное N max | + | - | + | + | - | + |
| Гидродинамическое давление на подводную часть плавучей системы минимальное N min | - | + | + | - | + | + |
Примечание: поперечный ветер действует поперек течения.
Якоря и якорные канаты следует рассчитывать на горизонтальные усилия, определяемые по формулам:
для верховых закреплений
S в = Wp+N max; (55)
для низовых закреплений
Sн = Wp-N min (56)
где Wp, N max, N min соответствуют формулам (31) - (35).
Минимальная длина якорного каната (расчалки) l min (в м) определяется из условия, чтобы канат походил к якорю горизонтально (рис. 83). Для этого длина якорных канатов принимается не менее 10-15 наибольших глубин воды на закрепляемом участке.
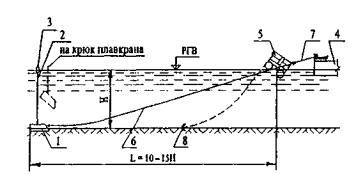
Рис. 83. Схема якорного закрепления плашкоута:
1 - железобетонный якорь-присос; 2 - строп; 3 - якорный буй; 4 - плашкоут; 5 - якорный плот с плавучим рымом; 6 - папильонажный канат; 7 - якорный канат (расчалка); 8 - весовой якорь (положение до сростки якорного и папильонажного каната)
Коэффициент надежности по назначению для стальных канатов принимают γn = 3,5 по отношению к разрывному усилию каната в целом. Ориентировочный диаметр каната (в см) можно определить по простой зависимости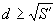 
, где S ' берется в тс, и определяется по формуле
S' = S/ cos α, (57)
где α - угол в плане между направлением течения реки и расчалкой (см. рис. 52).
Горизонтальное усилие на якорь адмиралтейского типа допускается принимать в пределах 5-6 весов якоря при песчаных и 8 - 12 весов якоря - при глинистых грунтах.
|
|
Горизонтальное усилие на железобетонный якорь-присос допускается принимать в пределах 1,3-1,6 весов якоря, но не более 70% предельного усилия, установленного при испытании якоря.
Пример 5. Выше в примере 2 для забивки железобетонных призматических свай сечением 35×35 см длиной 12 м (q 2 = 3,6 тс) подобран гидромолот Junttan марки ННК -4 с массой ударной части 4,0 т (q 1 = 6,3 тс). Произведем расчет плавучей системы для установки гусеничного копра РМ -20 фирмы Junttan (вес копра Рк = 40 тс = 392 кН), предназначенного для работы данного молота. Работы ведутся в IV ветровом районе (по карте районирования территории России СНиП 2.01.07-85*). Ширина зеркала воды в межень 440 м, скорость течения воды - 0,5 м/с. Расчетная высота волн - 1,0 м.
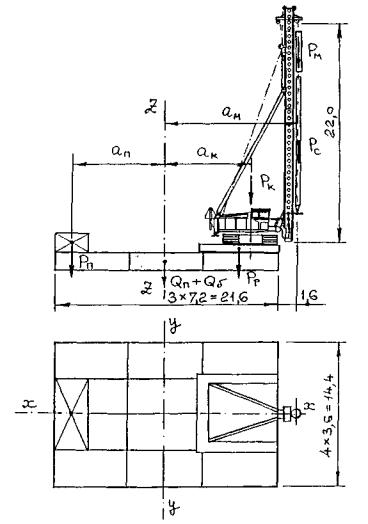
Рис. 84. Общий вид и расчетная схема плавучей системы с копром РМ -20 на 12 понтонах КС-63 (к примеру 5)
Для установки копра примем плашкоут из 12 понтонов КС-63 (3×4 шт.) размерами в плане 21,6×14,4 м, высотой борта 18 м (рис. 84).
Определим необходимый вес противовеса (регулировочного сухого балласта) исходя из условия, чтобы при копре с подвешенным молотом в рабочем состоянии (свая установлена в направляющие, ее вес не действует на копер) стрела копра была вертикальной, т.е. дифферент плавсистемы равен нулю:
ΣМz = 0; Р п ·a п -Рк·ак-Р м ·а м -Рр·ар = 0,
где Рр = 40 кН - вес металлической рамы под копер.
Отсюда
Р п= (Рк·ак+Р м ·а м +Рр·ар)/а п = (392×8,0+61,8×12,4+40×7,2)/9,0 = 466 кП.
Принимаем противовес из железобетонных плит объемом V п = 466/(9,81×2,4) = 20 м3.
|
|
Определим полный вес плавсистемы:
вес понтонов - Q п = (6,28+0,52)×9,81×12 = 800 кН;
вес остаточного балласта - Qo.б. = 21,6×14,4×0,1×9,81×1,0 = 305 кН;
веса копра с рамой, молота и сваи указаны выше.
ΣQ = 800+305+466+392+61,8+40+35 = 2100 кН.
Проверим плавсистему на плавучесть по формуле (41):
γΣV п = 1,0×9,81×12×45×0,9 = 4767 кН,
где γf = 0,9 - коэффициент надежности по нагрузке;
ΣQkн = 2100×2,0×1,1 = 4620 кН,
где γf = 1,1 - также коэффициент надежности по нагрузке.
Условие (41) выполняется, т.е. γΣV п > γΣkн.
При расчете плавсистемы на остойчивость вначале по формуле (44) определим среднюю осадку плашкоута:
t в = 2100×1,1/(0,97×21,6×14,4×9,81) = 0,78 м.
Положение центра тяжести плавсистемы найдем из уравнения суммы статических моментов всех сил относительно уровня днища плашкоута:
а = (800×0,9+305×0,05+466×2,3+392×7,0+61,8×16+40×2,1+35×8,0)/2100-0,78/2 = 2,42 м.
Моменты инерции плашкоута относительно осей х и у равны:
Iх = 21,6×14,43/12 = 5374 м4;
Iу = 14,4×21,63/12 = 12093 м4.
По формуле (43) определяем метацентрические радиусы (так как балластируемых понтонов в данном случае нет, Σin = 0):
ρх = 5374/235,3 = 22,8 м;
ρу = 12093/235,3 = 51,4 м,
где ΣVp = 21,6×14,4×0,78×0,97 = 235,3 м3.
Проверяем остойчивость плавсистемы по условию (42):
ρ min- а = 22,8-2,42 = 20,38 м > 0,
т.е. остойчивость обеспечивается.
Далее рассчитаем углы крена и дифферента плавсистемы по формуле (46). При этом имеем в виду, что поперечный крен постоянной нагрузкой не вызывается.
Согласно СТП 136-99 [25] нормативная ветровая нагрузка для IV ветрового района составляет w 0 = 0,48 кН/м2.
Значения коэффициента k, учитывающего изменение ветрового давления по высоте от уровня воды, составляют:
|
|
для плашкоута - 0,75;
для копра - 1,0;
для стрелы, молота, сваи - 1,25.
Аэродинамические коэффициенты для всех элементов, имеющих в данном случае сплошное прямоугольное сечение, с = 1,4.
Значения средней ветровой нагрузки, действующей поперек плавсистемы (без пульсационной составляющей, которая в данном случае не известна):
на плашкоут -
W 1 = w 0 kc = 0,48×0,75×1,4×21,6×(1,8 - 0,78) = 11,2 к11;
на копер - W 2 = 0,48×1,0×1,4×7×4 = 18,8 кН;
на стрелу - W 3 = 0,48×1,25×1,4×1,0×22 = 18,5 кН;
на молот - W 4 = 0,48×1,25×1,4×145 = 4,2 кН;
на сваю - W 5 = 0,48×1,25×1,4×0,35×12 = 3,5 кН.
Сумма моментов от поперечных ветровых нагрузок (рис. 85):
ΣМ вр = 11,2×(1,8-0,78)/2+18,8×3+18,5×12+4,2×15++ 3,5×6,5 = 370 кН·м.
По формуле (46):
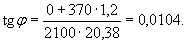
Дополнительная осадка, вызванная креном (формула (45)):
tx = 14,4×0,0104/2 = 0,075 м.
Как видим, дополнительная осадка в 75 мм не столь значительна. Отклонение оси сваи от вертикали на угол 0,01 также находится в допустимых пределах.
Рис. 85. Расчетная схема действия ветровой нагрузки при расчете плавсистемы на устойчивость
Значения средней ветровой нагрузки, действующей вдоль плавсистемы:
на плашкоут - W 1 = 14,4×11,2/21,6 = 7,5 кН;
на копер - W 2 = 5×18,8/7 = 13,4 кН;
на стрелу - W 3 = 18,5 кН;
на молот - W 4 = 0;
на сваю - W 5 = 0.
Сумма моментов от постоянных нагрузок:
ΣМ п = -466×0,9×9+(392×8+61,8×12,4+40×7,2)×1,1 = 837,5 кН·м.
Сумма моментов от временных нагрузок (включающих ветровые нагрузки и вес сваи):
ΣМ вр = 7,5×(1,8-0,78)/2+13,4×3+18,5×12+3,5×12,4×1,1 = 313,8 кН·м.
По формуле (46):
Дополнительная осадка, вызванная дифферентом:
ty = 21,6×0,0112/2 = 0,121 м.
Условия (47) соблюдены, так как по дифференту φ 1 = φ 2 = 2×(1,8-0,78)/21,6 = 0,094.
Далее рассчитаем корпус судна на прочность.
Наибольший изгибающий момент и поперечную силу в миделе определим по формуле (50):
M0 = [ γfpP п×(L -4 а п)+ γfp ×(1+ m)× Рк ×(L -4 ак)+ γfp ×(1+ m)×(PM + Pc)×
×(L -4 a м)+ γfpЕPр ×(L -4 aр)]/8 = [1,1×466×(21,6-4×9,0)+
+1,1×1,2×392×(21,6-4×8,0)+1,1×1,2×(61,8+35)×(21,6-4×
×12,4)+1,1×40×(21,6-4×7,2)]/8 = -2083 кН·м;
Q 0 = 1,1×466×(0,5-9,0/21,6) = 43 кН.
Для определения дополнительного изгибающего момента от волновых воздействий вначале определим коэффициенты в формуле (51):
k 0 = 1,24-2,0×14,4/21,6 = -0,093;
k 1 = 0,012;
k 2 = 2-20×0,77/21,6 = 1,287.
По формулам (51) и (52) определяем дополнительный изгибающий момент и поперечную силу в миделе судна при высоте волн 1,0 м:
Δ М = -0,093×0,012×1,287×0,97×14,4×21,62×1,0×9,81 = -91,8 кН·м;
Δ Q = 4×91,8/21,6 = 17 кН.
Суммарный изгибающий момент, действующий в одном понтоне:
M' = (М 0+Δ M)/4 = (-2083-92)/4 = -544 кН·м.
Суммарная поперечная сила, приходящаяся на один понтон:
Q' = (Q 0+Δ Q)/4 = (43+17)/4 = 15 кН
По графику на рис. 59, точка с координатами (М', Q') находится внутри предельной кривой, т.е. прочность корпуса судна обеспечена.
Наконец, рассчитаем мощность якорного закрепления плашкоута, имея в виду, что наибольшие усилия приходятся на верховые якоря.
Ветровая нагрузка расчетной интенсивности уже определена ранее при расчете на остойчивость (поперек плавсистемы, так как при работе плашкоут развернут большей стороной поперек течения реки):
Wp = ΣWi = 11,2+18,8+18,5+4,2+3,5 = 56,2 кН.
Лобовое давление воды по формуле (33) при скорости течения воды 0,5 м/с
Nл = 500×1,0×21,6×0,78×0,52 = 2106 Н.
Подсчитаем силу трения воды по поверхности подводной части плашкоута по формулам (34), (35):
N т = 0,17×21,6×(2×0,78+14,4)×0,52×9,81 = 144 Н.
Кроме того, учитываем нагрузку от волновых воздействий 300 Н/м для реки шириной до 500 м.
Суммарная гидродинамическая нагрузка на подводную часть плашкоута
N max= 2106+144+300×21,6 = 8730 Н.
Максимальная нагрузка на верховое якорное закрепление по формуле (55):
S в = 56,2+8,7 = 64,5 кН.
Усилие в одном канате расчалки при угле α = 30° по формуле (57)
S' = 64,5/(2×cos 30°) = 37 кН.
Ориентировочный диаметр каната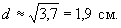 
Железобетонный якорь-присос берем весом Q л = 3,7/1,5 = 2,5 тс.