Пусть  и
и  – бесконечно малые при
– бесконечно малые при  .
.
Если  , то
, то  и
и  называются бесконечно малыми одного порядка;
называются бесконечно малыми одного порядка;
если  , то
, то  и называются бесконечно малой высшего порядка по сравнению с бесконечно малой
и называются бесконечно малой высшего порядка по сравнению с бесконечно малой  , что обозначается
, что обозначается  (читается: «
(читается: « равна o малому от
равна o малому от  »);
»);
если 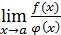 не существует, то бесконечно малые
не существует, то бесконечно малые  и
и  называются несравнимыми.
называются несравнимыми.
В частном случае, когда  , бесконечно малые
, бесконечно малые  и
и  называются эквивалентными,
называются эквивалентными,  . Если
. Если  , то бесконечно малую
, то бесконечно малую  можно представить в виде
можно представить в виде  . Для эквивалентных бесконечно малых выполняется свойство транзитивности, т.е. если
. Для эквивалентных бесконечно малых выполняется свойство транзитивности, т.е. если  , а
, а  , то
, то  .
.
Для более точного сравнения бесконечно малых функций  и
и  при
при  а в том случае, когда
а в том случае, когда  , т.е.
, т.е.  – бесконечно малая более высокого порядка, чем
– бесконечно малая более высокого порядка, чем  , одна из них, например
, одна из них, например  , сравнивается с различными функциями вида
, сравнивается с различными функциями вида  . Если для некоторого значения k оказывается, что
. Если для некоторого значения k оказывается, что  , то функция
, то функция  называется бесконечно малой k-го порядка относительно
называется бесконечно малой k-го порядка относительно  , а функция
, а функция  , эквивалентная функции
, эквивалентная функции  , называется главной частью функции
, называется главной частью функции  ,
,  .
.
Часто для количественной оценки малости функции функций  при
при  в качестве эталонов берутся функции
в качестве эталонов берутся функции  при
при  , причем k принимает любые вещественные значения. Такой набор эталонов простейшего вида образует как бы шкалу, удобную для сравнения бесконечно малых при (
, причем k принимает любые вещественные значения. Такой набор эталонов простейшего вида образует как бы шкалу, удобную для сравнения бесконечно малых при ( ). Если
). Если  , то такую шкалу образуют эталоны сравнения вида
, то такую шкалу образуют эталоны сравнения вида  . В общем случае в качестве эталонов сравнения выбирается некоторое множество функций
. В общем случае в качестве эталонов сравнения выбирается некоторое множество функций  , определенных на некотором интервале, примыкающем к точке a, и таких, что
, определенных на некотором интервале, примыкающем к точке a, и таких, что  , если
, если  .
.
Для эквивалентных бесконечно малых справедлива теорема: если  и
и  — бесконечно малые при
— бесконечно малые при  и
и  ,
, 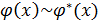 , а
, а  , то
, то
 и
и  ; (1)
; (1)
 и
и  ; (2)
; (2)
 . (3)
. (3)
Наличие набора эквивалентных бесконечно малых часто значительно упрощает вычисление пределов при раскрытии неопределенностей. Так, при 
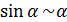 , (
, (
 , (
, (
 , (
, (
 , (
, (
 , (
, (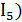
 ,
, 
 , (
, (
 , (
, (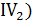
 , (
, (
 . (
. (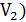
Аналогичные понятия вводятся для бесконечно больших функций  и
и  при
при  : если
: если  , то они называются бесконечно большими одного порядка; если
, то они называются бесконечно большими одного порядка; если 
 , то функция
, то функция  называется бесконечно большой высшего порядка по сравнению с функцией
называется бесконечно большой высшего порядка по сравнению с функцией  ; если
; если 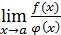 не существует, то функции
не существует, то функции  и
и  называют несравнимыми бесконечно большими.
называют несравнимыми бесконечно большими.
Эквивалентные бесконечно большие определяются точно так же, как эквивалентные, как эквивалентные бесконечно малые, т.е.  , если
, если  .
.
Если  , то бесконечно большая
, то бесконечно большая  называется бесконечно большой k-го порядка относительно бесконечно большой
называется бесконечно большой k-го порядка относительно бесконечно большой  , а функция
, а функция  , эквивалентная функции
, эквивалентная функции  , называется главной частью функции
, называется главной частью функции  .
.
Простейшие примеры эквивалентных бесконечно больших получаются из рассмотрения многочлена  :
:
при 
 ,
,  ,
, 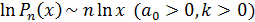 . (4)
. (4)
Для эквивалентных бесконечно больших справедливы соотношения (1)–(3).
Применение эталонов сравнения – источник приближенных формул. Если, например, функция  при
при  имеет главную часть
имеет главную часть 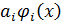 , где
, где  – постоянная, то
– постоянная, то  . Выделяя из функции
. Выделяя из функции  главную часть
главную часть  , получаем более точную формулу:
, получаем более точную формулу:  . Этот процесс можно продолжить. Если в результате приходят к формуле вида
. Этот процесс можно продолжить. Если в результате приходят к формуле вида

то говорят, что функция  обладает разложением порядка n относительно эталонов
обладает разложением порядка n относительно эталонов  . Пренебрегая слагаемым
. Пренебрегая слагаемым  , получаем приближенное выражение для функции
, получаем приближенное выражение для функции  при x, достаточно близких к a.
при x, достаточно близких к a.
Пример 1. Сравнить функции: 1)  и x при
и x при  ; 2)
; 2)  и
и  при
при 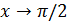 ; 3)
; 3)  и
и  при
при  .
.
Решение.  Данные функции при
Данные функции при  бесконечно малые. Составим их отношение и высчитаем его предел при
бесконечно малые. Составим их отношение и высчитаем его предел при  :
:

Следовательно, данные функции одного порядка малости.
2) При 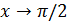 функции бесконечно малые и
функции бесконечно малые и

следовательно, функция  есть бесконечно малая высшего порядка по сравнению с
есть бесконечно малая высшего порядка по сравнению с  . А так как
. А так как 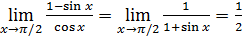 , то
, то  есть бесконечно малая второго порядка относительно
есть бесконечно малая второго порядка относительно  .
.
3) При 
 и
и  бесконечно большие одного порядка.
бесконечно большие одного порядка.
Пример 2. Сравнить функции  и
и  при
при  .
.
Решение. Поскольку  , то, учитывая, что
, то, учитывая, что  (см. соотношение
(см. соотношение 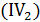 ), имеем
), имеем  .
.
Так как  (см. соотношение
(см. соотношение  ), а
), а  при
при  , имеем
, имеем  .
.
Тогда, используя соотношение (2), получаем, что

Следовательно, данные функции одного порядка малости, более того – эквивалентны.
Пример 3. Сравнить функции  и
и  при
при  .
.
Решение. Из равенства  следует, что
следует, что  при
при  (
( при
при  ). С другой стороны,
). С другой стороны,  при
при  ; следовательно,
; следовательно, 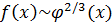 , т.е.
, т.е.  есть бесконечно большая порядка 3/2 относительно бесконечно большой
есть бесконечно большая порядка 3/2 относительно бесконечно большой  .
.
Пример 4. Выделить главную часть функции 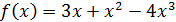 при: 1)
при: 1)  ; 2) при
; 2) при  .
.
Решение. При малых x поведение функции  будет определять то слагаемое, которое стоит в низшей степени. Поэтому вынесем за скобки малых x в первой степени:
будет определять то слагаемое, которое стоит в низшей степени. Поэтому вынесем за скобки малых x в первой степени:  . Выражение в скобках
. Выражение в скобках 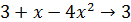 при
при  , следовательно, согласно соотношению (3)
, следовательно, согласно соотношению (3) 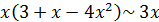 , и имеет место равенство
, и имеет место равенство  при
при  , где
, где  – главная часть функции
– главная часть функции  , а
, а  – бесконечно малая более высокого порядка, чем
– бесконечно малая более высокого порядка, чем  .
.
2) Заметим, что  ; следовательно, функция
; следовательно, функция  есть бесконечно малая в точке
есть бесконечно малая в точке  . В результате деления получим
. В результате деления получим 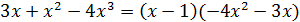 . Поскольку
. Поскольку  при
при  , то
, то  и
и  является главной частью функции
является главной частью функции  при
при  , и имеет место равенство
, и имеет место равенство  при
при  – бесконечно малая более высокого порядка, чем
– бесконечно малая более высокого порядка, чем 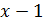 при
при  .
.
Пример 5. Выделить главную часть функции  при
при  .
.
Решение. Используем эквивалентное соотношение  , роль бесконечно малой
, роль бесконечно малой 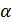 здесь играет
здесь играет  при
при  :
:


так как  при
при  . Итак,
. Итак,  при
при  .
.
Пример 6. Выделить главную часть функции  при
при 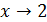 .
.
Решение. Выражение, стоящее под знаком корня, стремится к единице, поэтому его можно представить в виде суммы двух слагаемых – единица плюс бесконечно малая:  , тогда
, тогда  при
при 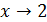 , так как
, так как 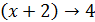 при
при 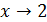 . Итак,
. Итак,  .
.
как  при
при  . Итак,
. Итак,  при
при  .
.
Пример 7. Выделить главную часть функции  при
при  .
.
Решение. Выражение, стоящее под знаком логарифма, стремится к единице при  , поэтому его можно представить в виде суммы единицы и бесконечно малой, причем роль бесконечно малой играет
, поэтому его можно представить в виде суммы единицы и бесконечно малой, причем роль бесконечно малой играет  . Тогда (см. соотношение
. Тогда (см. соотношение  )
)
 при
при  .
.
Следовательно,  при
при  .
.
Пример 8. Выделить главную часть функции  при
при 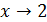 .
.
Решение. Так как выражение стоящее под знаком логарифма, стремится к единице при 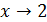 , то его можно представить следующим образом:
, то его можно представить следующим образом:  , где
, где  – бесконечно малая при
– бесконечно малая при  По формуле
По формуле  и соотношению (3) получим
и соотношению (3) получим  при
при 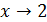 , отсюда
, отсюда 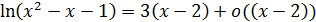 , где
, где  – бесконечно малая более высокого порядка, по сравнению с
– бесконечно малая более высокого порядка, по сравнению с 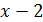 при
при 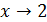 , т.е.
, т.е.  .
.
Пример 9. Выделить главную часть функции  при
при  .
.
Решение. Так как дробь  при
при  , то представим ее в следующем виде:
, то представим ее в следующем виде:
