Проекции с параллелями постоянной кривизны

· Параллели прямые линии. Описывается уравнениями, выраженными только в прямоугольной системе координат. Включает 4 класса проекций

a) Цилиндрические проекции (меридианы - равностоящие параллельные прямые, а параллели – параллельные прямые, ортогональные меридианам). Их общие уравнения х= f (φ) и y=βλ

Где β – параметр проекции

b) обобщенные цилиндрические проекции (меридианы – неравностоящие параллельние прямые, а параллели – параллельные прямые,ортогональные меридианам. Об. Ур-е х= f ₁(φ) и х= f₂ (λ)

c) Псевдоцилиндрические проекции (параллели – параллельные прямые, меридианы – кривые или прямые симметричные относительно среднего прямолинейного меридиана.

Об. Ур-я х= f ₁(φ) и х= f₂ (φ,λ)

d) цилиндрическо-конические проекции, в которых параллели изображаются пучком прямых, а меридианы – концентрическими окружностями.

· Конические окружности. Выражаются в системах плоских полярных и прямоугольных координат.

a) Конически епроекции (параллели – концентрические окружности, а меридианы – пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ пропорциональны углам между ними на поверхности эллипсоида (шара). В точке полюса Р имеется разрыв изображения. Ур-я

b) Обобщенные конические проекции (параллели – конц окружности, меридианы - пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ являются функциями этих углов на эллипсоиде (шаре). В точке полюса Р имеется разрыв.

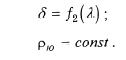
c) Псевдоконические проекции (параллели - концентрические окружности, меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

d) Азимутальные проекции (параллели -концентрические окружности, меридианы - пучок прямых, исходящих из центра окружности). В точке полюса отсутствует разрыв изображения. Углы между меридианами на проекции равны углам между ними на шаре (эллипсоиде). Плоские полярные координаты выражаются в функции полярных сфероидических (сферических) координат z=const, a=const. Уравнения

e) Обобщенные азимутальные проекции (параллели -концентрические окружности, меридианы - пучок прямых, исходящих из центра окружности, углы между ними являются функциями этих углов на эллипсоиде, в точке полюса отсутствует разрыв изображения. Меридианы с долготами 0 и 360 совпадают). Уравнения

f) Псевдоазимутальные проекции. Параллели – конц. Окр, в точке полюса нет разрыва изображения. Меридианы с долготами 0 и 360 совпадают и являются либо прямыми либо кривыми, в каждой точке которых они имеют одинаковую кривизну, остальные меридианы – прямые или кривые линии. Уравнения

· Эксцентрические окружности. Выражаются в плоских и прямоугольных координатах.

a) Поликонические проекции в широком смысле(параллели – эксцентрические окружности, центры которых находятся на среднем меридиане, а меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

b) Поликонические проекции в узком смысле. Накладывается еще два условия: полярный радиус p=N ctg φ. Частный масштаб длин на среднем меридиане имеет постоянное значение m₀=k, в частности m₀=1.

2) Картографические проекции с параллелями переменной кривизны

· Полиазимутальные проекции и обобщенные полиазимутальные проекции

a) Полиазимутальные проекции. Параллели-эллипсы, меридианы – пучок прямых или кривых, исходящих из центра эллипсов, в точке полюса отсутствует разрыв изображения. Общие уравнения

b) Обобщенные полиазимутальные (параллели – кривые произвольной кривизны, а меридианы пучок прямых или кривых, исходящих из точки полюса, в котором нет разрыва изображения). Общие уравнения

· Обобщенные поликонические, различающиеся изображением параллелей; в виде – эллипсов, парабол, гипербол и параллелями произвольной кривизны, меридианы изображаются кривыми линиями. Обобщенные уравнения

· Полицилиндрические проекции. Параллели и меридианы изображаются кривыми произвольной или заданной кривизны (эллипсами, параболами и гиперболами)

Общие уравнения

· Проекции произвольных поверхностей, картографическая сетка которых отражает форму картографических поверхностей. Обобщение азимутальных, цилиндрических, конических и др проекций.

· Проекции для создания аноморфированных карт, обладающие дополнительными функциональными возможностями:

a) Варивалентные проекции

b) Переменно-масштабные проекции (при сохранении общего масштаба карты достигается сжатие или растяжение изображения на ее отдельных участках

c) Проекции с измененной метрикой пространства (исп эвклидова метрика и др метрики)