Принятая при данной картографической проекции система изображения сети меридианов и параллелей называется картографической сеткой.
Картографическая сетка для каждого класса проекций, в которой изображение меридианов и параллелей имеет наиболее простой вид, называется нормальной сеткой.
По способу построения картографической нормальной сетки все проекции делятся на конические, цилиндрические, азимутальные, условные и др.
Конические проекции. Проектирование координатных линий Земли производят по какому-либо из законов на внутреннюю поверхность описанного или секущего конуса, а затем, разрезав конус по образующей, разворачивают его на плоскость.
Для получения нормальной прямой конической сетки делают так, чтобы ось конуса совпадала с земной осью PNР S (рис, 33). В этом случае меридианы изображаются прямыми линиями, исходящими из одной точки, а параллели — дугами концентрических окружностей. Если ось конуса располагают под углом к земной оси, то такие сетки называют косыми коническими.
В зависимости от закона, выбранного для построения параллелей, конические проекции могут быть равноугольными, равновеликими и произвольными. Конические проекции применяются для географических карт.
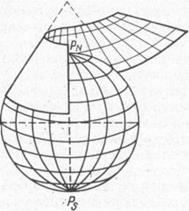
Рис. 33
Цилиндрические проекции. Картографическую нормальную сетку получают путем проектирования координатных линий Земли по какому-либо закону на боковую поверхность касательного или секущего цилиндра, ось которого совпадает с осью Земли (рис.34), и последующей развертки по образующей на плоскость.
В прямой нормальной проекции сетка получается из взаимно перпендикулярных прямых линий меридианов Л, В, С, D, F, G и параллелей аа',bb',сс При этом без больших искажений будут изображены участки поверхности экваториальных районов (см, окружность К и ее проекцию К на рис. 34), но участки полярных районов в этом случае не могут быть спроектированы.
Если повернуть цилиндр так, чтобы ось его расположилась в плоскости экватора, а поверхность его касалась полюсов, то получается поперечная цилиндрическая проекция (например, поперечная цилиндрическая проекция Гаусса). Если цилиндр поставить под другим углом к оси Земли, то получаются косые картографические сетки. На этих сетках меридианы и параллели изображаются кривыми линиями.


Рис. 34
Азимутальные проекции. Нормальную картографическую сетку получают проектированием координатных линий Земли на так называемую картинную плоскость Q (рис. 35) — касательную к полюсу Земли. Меридианы нормальной сетки на проекции имеют вид радиальных прямых, исходящих из. центральной точки проекции PN под угла- ми, равными соответствующим углам в натуре, а параллели — концентрическими окружностями с центром в полюсе. Картинную плоскость можно располагать в любой точке земной поверхности, и точку касания называют центральной точкой проекции и принимают за зенит.
Азимутальная проекция зависит от того, какими радиусами проводятся параллели. Подчиняя радиусы той или иной зависимости от широты, получают различные азимутальные проекции, удовлетворяющие условиям либо равноугольности, либо равновеликости.
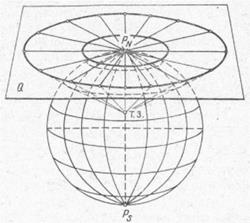
Рис. 35
Перспективные проекции. Если картографическую сетку получают проектированием меридианов и параллелей на плоскость по законам линейной перспективы из постоянной точки зрения Т.З. (см. рис. 35), то такие проекции называют перспективными. Плоскость можно располагать на любом расстоянии от Земли или так, чтобы она касалась ее. Точка зрения должна находиться на так называемом основном диаметре земного шара или на его продолжении, причем картинная плоскость должна быть перпендикулярна основному диаметру.
Когда основной диаметр проходит через полюс Земли, проекция называется прямой или полярной (см. рис. 35); при совпадении основного диаметра с плоскостью экватора проекция называется поперечной или экваториальной, а при других положениях основного диаметра проекции называются косыми или горизонтальными.
Кроме того, перспективные проекции зависят от расположения точки зрения от центра Земли на основном диаметре. Когда точка зрения совпадает с центром Земли, проекции называются центральными или гномоническими; когда точка зрения находится на поверхности Землистереографическими; при удалении точки зрения на какое-либо известное расстояние от Земли проекции называются внешними, и при удалении точки зрения в бесконечность —ортографическими.
На полярных перспективных проекциях меридианы и параллели изображаются аналогично полярной азимутальной проекции, но расстояния, между параллелями получаются разными и обусловлены положением точки зрения на линии основного диаметра.
На поперечных и косых перспективных проекциях меридианы и параллели изображаются в виде эллипсов, гипербол, окружностей, парабол или прямых линий.
Из особенностей, свойственных перспективным проекциям, следует отметить, что на стереографической проекции любой круг, проведенный на земной поверхности, изображается в виде окружности; на центральной проекции всякий большой круг, проведенный на земной поверхности, изображается в виде прямой линии, в связи с чем в некоторых частных случаях эту проекцию представляется целесообразным применять в навигации.
Условные проекции. К этой категории относятся все проекции, которые по способу построения нельзя отнести ни к одному из перечисленных выше видов проекций. Они обычно удовлетворяют каким-нибудь заранее поставленным условиям, в зависимости от тех целей, для которых требуется карта. Число условных проекций не ограничено.
Небольшие участки земной поверхности до 85 км можно изобразить на плоскости с сохранением на них подобия нанесенных фигур и площадей. Такие плоские изображения небольших участков земной поверхности, на которых искажениями практически можно пренебрегать, называются планами.
Планы обычно составляют без всяких проекций путем непосредственной съемки и на них наносят все подробности снимаемого участка.
Из рассмотренных выше проекций в судовождении в основном применяются: равноугольная, цилиндрическая, азимутальная перспективная, гномоническая и азимутальная перспективная стереографическая.