Определение объема выборки для оценки математического ожидания

Чтобы определить объем выборки, необходимый для оценки математического ожидания генеральной совокупности, следует учесть величину ошибки выборочного исследования и доверительный уровень. Еще необходима дополнительная информация о величине среднего квадратического отклонения.

Для того чтобы вывести формулу, позволяющую вычислить объем выборки, вспомним формулу:

,

где Z — критическое значение случайной величины, имеющей стандартизированное нормальное распределение.

Величина, добавляемая и вычитаемая из ,равна половине длины доверительного интервала. Она определяет меру неточности оценки, возникающей вследствие ошибки выборочного исследования, которая обозначается символом ε и вычисляется по формуле

(9)

Следовательно, объем выборки п определяется по формуле:

(10)

Таким образом, для определения объема выборки необходимо знать три параметра:

• величину Z, являющуюся критическим значением стандартизованного нормального распределения[3]

• приемлемую ошибку выборочного исследования ε;

• средне квадратическое отклонение σ.

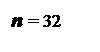
Рис. 3. Выборочные распределения средних арифметических, построенные по 500 выборкам с объемами п = 1; 2; 4 и 32, извлеченным из нормально распределенной генеральной совокупности

На практике вычислить эти величины непросто. Как определить доверительный уровень и ошибку выборочного исследования? Обычно ответить на этот вопрос могут лишь эксперты в предметной области (т.е. люди, понимающие смысл оцениваемых величин). Как правило, доверительный уровень равен 95% (в этом случае Z = 1,96). Если требуется поднять доверительный уровень, обычно выбирают величину, равную 99%. Если можно ограничиться более низким доверительным уровнем, выбирают 90%. Определяя ошибку выборочного исследования, не стоит думать о ее величине (в принципе, любая ошибка нежелательна). Следует задать такую ошибку, чтобы полученные результаты допускали разумную интерпретацию.

Кроме доверительного уровня и ошибки выборочного исследования, необходимо знать стандартное отклонение генеральной совокупности. К сожалению, этот параметр для потребителя почти никогда не известен. В некоторых случаях стандартное отклонение генеральной совокупности можно оценить на основе результатов предшествующей эксплуатации. В других ситуациях опытный менеджер по качеству может учесть размах выборки и распределение случайной переменной. Например, если генеральная совокупность имеет нормальное распределение, ее размах приближенно равен 6σ (т.е. ± 3σ в окрестности математического ожидания). Следовательно, стандартное отклонение приближенно равно одной шестой части, диапазона. Если величину σ невозможно оценить таким способом, необходимо спланировать и выполнить экспериментальные проверки.

Чтобы продемонстрировать применение этого подхода, рассмотрим простейший пример.

Пример 1. С помощью выборочного метода необходимо оценить средний стаж работы служа­щих крупной фирмы. Предполагается, что он подчиняется нормальному закону, и по результатам предыдущих исследований аналогичных организаций известно, что стан­дартное отклонение σ равно 2,70 года. Необходимо установить объем выборки с 95%-м доверительным уровнем и погрешностью, не превышающей величины 0,5 года.

Решение. По формуле (10) получаем:

Следовательно, п = 113, поскольку дробные результаты, как правило, округляют с избытком до ближайшего целого.

Ответ. Чтобы с вероятностью 0,95 и ε = 0,5 года определить средний стаж работы служа­щих крупной фирмы, необ­ходимо обследовать не менее 113 служащих.

Для этого же примера при 95% -м доверительном уровне определите, как изменится объем выборки при следующих условиях:

σ=2,7; ε = 0,1; п = 2801?