Рассматриваемая ситуация характерна для производителя, когда налажен массовый выпуск продукции с установленными техническими характеристиками. Менеджер по качеству обязан организовать выборочный контроль качества выпускаемой продукции и периодически анализировать результаты выходного контроля, не допуская отклонения определяющих параметров качества за допустимые пределы. Для потребителя данная ситуация маловероятна.
Методика построения доверительного интервала состоит в следующем. Из выражения (2) следует, величина доверительного интервала зависит от статистической нестабильности самой генеральной совокупности (параметр σ), объема выборки n и коэффициента t, который, в свою очередь, зависит от закона распределения генеральной совокупности и ее параметров μ или σ.
В случае распределения генеральной совокупности по нормальному закону и известном стандартном отклонении σ доверительный интервал для математического ожидания генеральнойсовокупности μ имеет границы:
,[2] (3)
где стандартизованная (выраженная в долях σ) величина Z соответствует определенному доверительному уровню и определяется из таблиц нормального распределения (табл. 1).
Например, доверительному уровню, равному 95% (α=0,05), соответствует Z = ±1,96. Если требуется построить интервал, доверительный уровень которого равен 99%, то величина Z приближенно равна 2,58. Для 90% уровня надежности Z = ±1,65.
Интервал, выраженный формулой (3), можно представить с 95 %-м уровнем вероятности следующим образом:
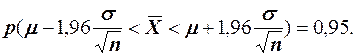(4)
Небольшое алгебраическое преобразование в двойном неравенстве даст:
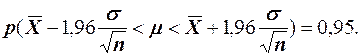(5)
Рассмотрим гипотетический пример. Допустим, что математическое ожидание μ исследуемого параметра генеральной совокупности равно 1000 размерных единиц (это могут быть граммы, метры, секунды или любые другие физические величины). Предположим, что из генеральной совокупности извлекается выборка, состоящая из 25 единиц продукции, измеряется действительное значение физической величины каждого образца выборки и вычисляется среднее значение анализируемой физической величины для всех 25 представителей, которое равно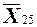 
=996,75 ед, а истинное стандартное отклонение σ = 15.
|
|
Воспользовавшись результатами (4) и (50), получаем, что интервал для оценки математического ожидания μ имеет границы:
996,75± 1,96×15/ 
Откуда
994,12 < μ < 1005,88.
Поскольку математическое ожидание генеральной совокупности μ равно 1000, оно попадает в этот интервал, и, следовательно, данная выборка дает правильную оценку (рис. 2, доверительный интервал 1).
Продолжим анализ нашего гипотетического примера. Допустим, что выборочное среднее некоей выборки объема п = 25, равно 1001,50. Доверительный интервал, построенный по этой выборке, имеет границы равные 1001,50 ± 1,96×15/ , т.е. 1001,50±5,88 (доверительный интервал 2 на рис. 2).
Таким образом,
995,62 ≤ μ £ 1007,38.
Поскольку математическое ожидание генеральной совокупности μ равно 1000, оно попадает в этот интервал, и, следовательно, данная оценка является правильной.
Возникает впечатление, что выборки, имеющие объем п = 25, всегда приводят к правильным оценкам математического ожидания генеральной совокупности μ. Чтобы опровергнуть это, рассмотрим третий гипотетический пример. Допустим, что 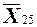=992 ед. Интервал, предложенный для оценки математического ожидания μ, имеет границы: 992±1,96 × 15 , т.е. 992 ±5,88. Таким образом, в данном случае имеем:
|
|
986,12 ≤ μ £ 997,88 (доверительный интервал 3 на рис. 2).
Эта оценка неверна,поскольку математическое ожидание генеральной совокупности μ равна 1000 и не попадает в этот интервал (см. рис. 2, доверительный интервал 3). Таким образом, для некоторых выборок эта оценка верна, а для некоторых — нет. Кроме того, на практике, как правило, из генеральной совокупности извлекается только одна выборка. Следовательно, поскольку математическое ожидание генеральной совокупности μ не известно, невозможно сказать, верна полученная интервальная оценка или нет.
Чтобы разрешить эту дилемму, необходимо определить долю выборок, позволяющих правильно оценить математическое ожидание генеральной совокупности μ. Для этого следует исследовать еще две гипотетические выборки, средние значения которых равны 994,12 и 1005,88 соответственно.
Если 
= 994,12, мы получаем интервал 994,12 ±1,96×15/ , т.е. 994,12 ±5,88. Это приводит к оценке
988,24 ≤ μ £ 1000 (доверительный интервал 4 на рис. 2).
Поскольку математическое ожидание генеральной совокупности μ, равное 1000, является верхней границей интервала, эта оценка верна.
Если = 1005,88, мы получаем интервал 1005,88 ± 1,96×15/ , т.е. 1005,88±5,88. Это приводит к оценке
1000 ≤ μ £ 1011,76 (доверительный интервал 5 на рис. 2).
Поскольку математическое ожидание генеральной совокупности μ, равное 1000, является нижней границей интервала, эта оценка верна.
Таким образом, если выборочное среднее изменяется в диапазоне от 994,12 до 1005,88 ед., математическое ожидание генеральной совокупности лежит где-то внутри этого соответствующего доверительного интервала. Вероятность того, что это значение лежит в интервале с границами 994,12 и 1005,88, равна 95%. Следовательно, 95% средних значений всех выборок, имеющих объем n = 25, позволяют правильно оценить математическое ожидание генеральной совокупности, а 5% — нет.
|
|
На практике, как правило, из генеральной совокупности извлекается только одна выборка, а математическое ожидание генеральной совокупности μ не известно. По этой причине невозможно гарантировать, что некий конкретный доверительный интервал содержит величину μ. Можно лишь утверждать, что вероятность этого события равна 95%.
В некоторых ситуациях желательно иметь более высокий доверительный уровень, а следовательно, более высокую точность оценки величины μ (например, 99%). Но иногда можно ограничиться и менее точной оценкой (например, 90%),
Как правило, доверительный уровень обозначают следующим образом: (1- α)×100%, где величина α представляет собой площадь, ограниченную хвостом распределения, выходящим за пределы доверительного интервала. Величину α называют уровнем значимости доверительного интервала. Кроме того, в качестве синонима для доверительного уровня иногда употребляется выражение «доверительная вероятность ». Площади, ограниченные как левым, так и правым хвостами распределения, выходящими за пределы доверительного интервала, равны α/2 (см. рис.1).
Возникает вопрос, почему бы не построить интервал, доверительный уровень которого был бы очень близок к 100%. Это нецелесообразно, поскольку такой доверительный интервал оказался бы слишком широким, а оценка математического ожидания — слишком неточной. Разумеется, вероятность того, что математическое ожидание лежит в этом интервале, очень высока, однако для принятия решения этот факт практически бесполезен.
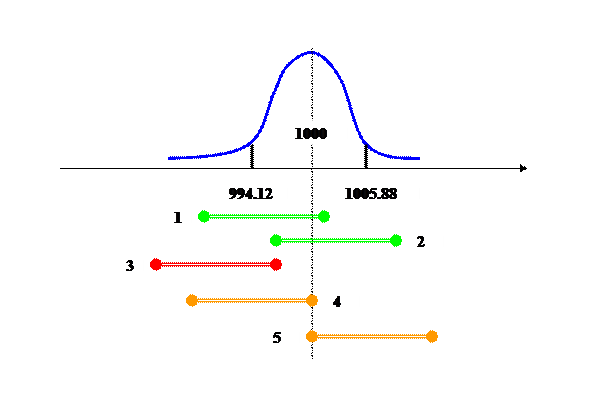
Рис. 2. Доверительные интервальные оценки математического ожидания генеральной совокупности, полученные по пяти разным выборкам объема n = 25, извлеченным из генеральной совокупности с параметрами μ= 1000 и σ = 15