Поправочный коэффициент можно также применять для определения объема выборки, извлеченной из конечной генеральной совокупности без возвращения. Например, при оценке математического ожидания выборочная ошибка вычисляется по следующей формуле:
.
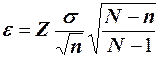При оценке доли признака ошибка выборочного исследования равна
.
Чтобы вычислить объем выборки для оценки математического ожидания или доли признака, применяются формулы (10) и (12):
и 
где n — объем выборки без учета поправочного коэффициента для конечной генеральной совокупности.
Применение поправочного коэффициента приводит к следующей формуле:
(19)
Пример 4.
Для оценки математического ожидания при N = 5000; ε =5; s = 25 и Z = 1,96 (для доверительного уровня, равного 95%) необходимо определить объем повторной и бесповторной выборки.
Решение.
По формуле (10) объем выборки с повторением (с возвращением) выборки равен:
т.е. объем выборки должен быть равен 97, т.к. выборка – целое число.
Используя формулу (19), получаем:
,
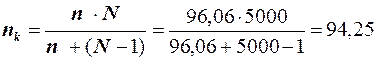т.е. когда выборки извлекаются без возвращения, с учетом конечности генеральной совокупности, ее размер уменьшается и для данного примера он равен 95.
Пример 5.
Для оценки доли признака при N = 5000; ε =0,07; p =0,15 и Z = 1,96 (для доверительного уровня, равного 95%) необходимо определить объем повторной и бесповторной выборки.
Решение.
По формуле (12) объем выборки с повторением равен:
, т.е. n = 100.
Применяя формулу (19), получаем:
, что n = 99.
Задачи и упражнения к разделу VII
Задача 1.
Предположим, что 
=75, S = 24, n = 36 и N = 200, причем выборка получена путем извлечения без возвращения. Постройте 95%-й доверительный интервал для математического ожидания и конечной генеральной совокупности. 67,63 £ m £ 82,37
Задача 2.
Допустим, что объем генеральной совокупности равен 1000, а стандартное отклонение равно 20. Какой объем выборки необходим, если выборка повторная (бесповторная), доверительный уровень равен 95%, а выборочная ошибка равна ±5. 61,46 (57,9589494)
Задача 3.
Инспектор отдела технического контроля на фабрике, производящей электрические лампочки, желает оценить среднюю продолжительность работы лампочек из крупной партии. Стандартное отклонение этой величины известно и равно 100 часов. Предположим, что партия состоит из 2000 электрических лампочек, а выбор выполняется без возвращения.
1. Постройте 95%-ный доверительный интервал для средней продолжительности работы лампочек из указанной партии, если средняя продолжительность работы 50 лампочек, принадлежащих выборке, извлеченной из партии, равно 350 часов. 322,6238≤ µ ≤ 377,3762
2. Определите объем выборки, необходимый для оценки средней продолжительности работы лампочек, если стандартное отклонение равно ±20 часов, а доверительный уровень равен 95%. 92
3. Как изменятся ответы к вопросам 1 и 2, если партия состоит из 1000 лампочек?
322,9708≤ µ ≤ 377,0297
Задача 4.
Служба контроля Энергосбыта провела выборочную проверку расхода электроэнергии жителями одного из многоквартирных домов. Было выбрано 10 квартир и определено, что расход электроэнергии (кВт /ч) в течение одного из летних месяцев равен: 125; 78; 102; 140; 90; 45; 50; 125; 115; 112.
С вероятностью 0,95 определите доверительный интервал для оценки среднего расхода электроэнергии на 1 квартиру во всем доме при условии, что в доме 70 квартир, а выбор был: а) повторным; б) бесповторным.
а) 75,20≤ µ ≤ 121,20;
б) 76,76≤ µ ≤ 119,64.
.
Таблица 1
Значения функции
Определяет вероятность попадания случайной величины X, подчиненной нормальному закону, в симметричный отрезок (- Z, Z)
| x | ||||||||||
| 1.0 | 0. 6827 | 7109. | ||||||||
| 1.1 | 0. 7287 | |||||||||
| 1.2 | 0. 7699 | |||||||||
| 1.3 | 0. 8064 | |||||||||
| 1.4 | 0. 8385 | |||||||||
| 1.5 | 0. 8664 | |||||||||
| 1.6 | 0. 8904 | |||||||||
| 1.7 | 0.9 1087 | |||||||||
| 1.8 | 0.9 2814 | |||||||||
| 1.9 | 0.9 4257 | |||||||||
| 2.0 | 0.9 54501 | |||||||||
| 2.1 | 0.9 6427 | |||||||||
| 2.2 | 0.9 7219 | |||||||||
| 2.3 | 0.9 7855 | |||||||||
| 2.4 | 0.9 8360 | |||||||||
| 2.5 | 0.9 8758 | |||||||||
| 2.6 | 0.9 9068 | |||||||||
| 2.7 | 0.9 9307 | |||||||||
| 2.8 | 0.9 9489 | |||||||||
| 2.9 | 0.9 9627 | |||||||||
| 3.0 | 0.9 9730 | |||||||||
| 3.1 | 0.9 9806 | |||||||||
| 3.2 | 0.9 9863 | |||||||||
| х |