Всегда и во всех сферах своей деятельности человек принимал решения. Важная область принятия решений связана с производством. Чем больше объем производства, тем труднее принять решение и, следовательно, легче допусить ошибку. Возниает естественный вопрос: нельзя ли во избежание таких ошибок использовать ЭВМ?
Ответ на этот вопрос дает наука, называемая кибернетика. Кибернетика (произошло от греческого "kybernetike" - искусство управления) - наука об общих законах получения, хранения, передачи и переработки информации.
Важнейшей отраслю кибернетики является экономическая кибернетика - наука, занимающаяся приложением идей и методов кибернетики к экономическим системам.
Экономическая кибернетика использует совокупность методов исследования процессов управления в экономике, включая экономико-математические методы.
В настоящее время применение ЭВМ в управлении производством достигло больших масштабов. Однако, в большинстве случаев с помощью ЭВМ решают так называемые рутинные задачи, то есть задачи, связанные с обработкой различных данных, которые до применения ЭВМ решались так же, но вручную. Другой класс задач, которые могут быть решены с помощью ЭВМ - это задачи принятия решений. Чтобы использовать ЭВМ для принятия решений, необходимо составить математическую модель. Так ли необходимо применение ЭВМ при принятии решений? Возможности человека достаточно разнообразны. Если их упорядочить, Так уж устроен человек, что того, чем он обладает, ему мало. И начинается бесконечный процесс увеличения его возможностей. Чтобы больше поднять, появляется одно из первых изобретений - рычаг, чтобы легче перемещать груз - колесо. В этих орудиях пока еще используется только энергия самого человека. Со временем начинается применение внешних источников энергии: пороха, пара, электричества, атомной энергии. Невозможно оценить, насколько используемая энергия внешних источников превышает сегодня физические возможности человека.
Что же касается умственных способностей человека, то, как говорится, каждый недоволен своим состоянием, но доволен своим умом. А можно ли сделать человека умнее, чем он есть? Чтобы ответить на этот вопрос, следует уточнить, что вся интеллектуальная деятельность человека может быть подразделена на формализуемую и неформализуемую.
Формализуемой называют такую деятельность, которую выполняют по определенным правилам. Например, выполнение расчетов, поиск в справочниках, графическаие работы, несомненно могут быть поручены ЭВМ. И как все, что может делать ЭВМ, она это делает лучше, то есть быстрее и качественнее, чем человек.
Неформализуемой называют такую деятельность, которая происходит с применением каких-либо неизвестныхы нам правил. Мышление, соображение, интуиция, здравый смысл - мы пока еще не знаем, что это такое, и естественно, все это нельзя поручить ЭВМ, хотя бы потому, что мы просто не знаем, что поручать, какую задачу поставить перед ЭВМ.
Разновидностью умственной деятельности является принятие решений.
Принято считать, что принятие решений относится к неформализуемой деятельности. Однако это не всегда так. С одной стороны, мы не знаем, как мы принимаем решение. И объяснеие одних слов с помощью других типа "принимаем решение с помощью здравого смысла" ничего не дает. С другой стороны, значительное число задач принятия решений может быть формализовано. Одним из видов задач принятия решений, которые могут быть формализованы, являются задачи принятия оптимальных решений, или задачи оптимизации. Решение задачи оптимизации производится с помощью математических моделей и применения вычислительной техники.
Современные ЭВМ отвечают самым высоким требованиям. Они способны выполнять миллионы операций в секунду, в их памяти могут быть все необходимые сведения, комбинация дисплей-клавиатура обеспечивает диалог человека и ЭВМ. Однако не следует смешивать успехи в создании ЭВМ с достижениями в области их применения. По сути, все что может ЭВМ - это по заданной человеком программе обеспечить преобразование исходных данных в результат. Надо четко себе представлять, что ЭВМ решения не принимает и принимать не может. Решение может принимать только человек-руководитель, наделенный для этого определенными правами. Но для грамотного руководителя ЭВМ является великолным помощником, способным выработать и предложить набор самых различных вариантов решений. А из этого набора человек выберет тот вариант который с его точки зрения окажется более пригодным. Конечно, далеко не все задачи принятия решений можно решить с помощью ЭВМ. Тем не менее, даже если решение задачи на ЭВМ и не заканчивается полным успехом, то все равно оказывается полезным, так как способствует более глубокому пониманию этой задачи и более строгой ее постановке.
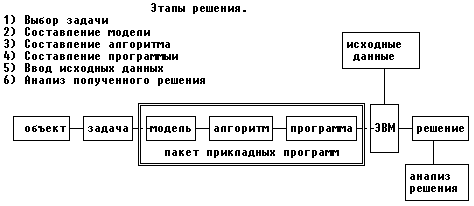
Чтобы человеку принять решение без ЭВМ, зачастую ничего не надо. Подумал и решил. Человек, хорошо или плохо, решает все возникающие перед ним задачи. Правда никаких гарантий правильности при этом нет. ЭВМ же никаких решений не принимает, а только помогает найти варианты решений. Данный процесс состоит из следующих этапов:
Выбор задачи.
Решение задачи, особенно достаточно сложной - достаточно трудное дело, требующее много времени. И если задача выбрана неудачно, то это может привести к потере времени и разочарованию в применении ЭВМ для принятия решений. Каким же основным требованиям должна удовлетворять задача?
А. Должно существовать как минимум один вариант ее решения, ведь если вариантов решения нет, значит выбирать не из чего.
Б. Надо четко знать, в каком смысле искомое решение должно быть наилучшим, ведь если мы не знаем чего хотим, ЭВМ помочь нам выбрать наилучшее решение не сможет.
Выбор задачи завершается ее содержательной постановкой. Необходимо четко сформулировать задачу на обычном языке, выделить цель исследования, указать ограничения, поставить основные вопросы на которые мы хотим получить ответы в результате решения задачи.
Здесь следует выделить наиболее существенные черты экономического объекта, важнейшие зависимости, которые мы хотим учесть при построении модели. Формируются некоторые гипотезы развитиця объекта исследования, изучаются выделеные зависимости и соотношения. Когда выбирается задача и производится ее содержательная постановка, приходится иметь дело со специалистами в предметной области (инженерами, технологами, конструкторами и. т. д.). Эти специалисты, как правило, прекрасно знают свой предмет, но не всегда имеют представление о том, что требуется для решения задачи на ЭВМ. Поэтому, содержательная постановка задачи зачастую оказывается перенасыщенной сведениями, которые совершенно излишни для работы на ЭВМ.
Составление модели
Под экономико-математической моделью понимается математическое описание исследуемого экономического объекта или процесса, при котором экономические закономерности выражены в абстрактном виде с помощью математических соотношений.
Основные принципы составления модели сводятся к следующим двум концепциям:
1. При формулировании задачи необходимо достаточно широко охватить моделируемое явление. В противном случае модель не даст глобального оптимума и не будет отражать суть дела. Опасность состоит в том, что оптимизация одной части может осуществляться за счет других и в ущерб общей организации.
2. Модель должна быть настолько проста, насколько это возможно. Модель должна быть такова, чтобы ее можно было оценить, проверить и понять, а результаты полученные из модели должны быть ясны как ее создателю, так и лицу, принимающему решение. На практике эти концепции часто вступают в конфликт, прежде всего из-за того, что в сбор и ввод данных, проверку ошибок и интерпретацию результатов включается человеческий элемент, что ограничивает размеры модели, которая может быть проанализирована удовлетворительно. Размеры модели используются как лимитирующий фактор, и если мы хотим увеличить широту охвата, то приходится уменьшать детализацию и наоборот.
Введем понятие иерархии моделей, гдте широта охвата увеличивается, а детализация уменьшается по мере того, как мы переходим на более высокие уровни иерархии. На более высоких уровнях в свою очередь формируются ограничения и цели для более низких уровней.
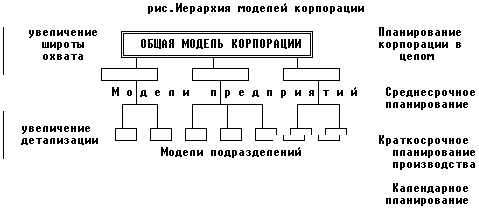
При построении модели горизонт планирования в основном увеличивается с ростом иерархии. Если модель долгосрочного планирования всей корпорации может содержать моло каждодневных текущих деталей то модель планирования производства отдельного подразделеия состоит в основном из таких деталей.
При формулировании задачи необходимо учитывать следующие три аспекта:
1) Исследуемые факторы: Цели исследования определены довольно свободно и в большой степени зависят от того, что включено в модель. В этом отношении Легче инженерам, так как исследуемые факторы у них обычно стандартны, а целевая функция выражается в терминах максимума дохода, минимума затрат или, возможно, минимума потребления какого-нибудь ресурса. В то же время социологи, к примеру, обычно задаются целью "общественной полезности" или в этом роде и оказываются в сложном положении, когда им приходится приписывать определенную "полезность" различным действиям, выражая ее в математической форме.
2) Физические границы: Пространственные аспекты исследования требуют детального рассмотрения. Если производство сосредоточено более чем в одной точке, то необходимо учесть в модели соответствующие распределительные процессы. Эти процессы могут включать складирование, транспортировку, а также задачи календарного планирования иещения оборудования.
3) Временные границы: Временные аспекты исследования приводят к сдерьезной дилемме. Обычно горизонт планирования хорошо известен, но надо сделать выбор: либо моделировать систему в динамике, с тем, чтобы получить временные графики, либо моделировать статическое функционирование в определенный момент времени. Если моделируется динамический (многоэтапный) процесс, то размеры модели увеличиваются соответственно числу рассматриваемых приодов времени (этапов). Такие модели обычно идейно просты, так что основная трудность заключается скорее в возможности решить задачу на ЭВМ за приемлемое время, чем в умении интерпретировать большой объем выходных данных. с Зачастую бывает достаточно построить модель системы в какой-то заданный момент времени, например в фиксированный год, месяц, день, а затем повторять расчеты через определенные промежутки времени. Вообще, наличие ресурсов в динамической модели часто оценивается приближенно и определяется факторами, выходящими за рамки модели. Поэтому необходимо тщательно проанализировать, действительно ли необходимо знать зависимость от времени изменения характеристик модели, или тот же результат можно получить, повторяя статические расчеты для ряда различных фиксированных моментов.
Составление алгоритма.
Алгоритм - это конечный набор правил, позволяющих чисто мехаически решать любую конкретную задачу из некоторого класса одотипных задач. При этом подразумевается:
а. - исходные данные могут изменяться в определеных пределах: {массовость алгоритма}
б. - процесс применения правил к исходным данным (путь решения задачи) определен однозначно: {детерминированность алгоритма}
в. - на каждом шаге процесса применения правил известно, что считать результатом этого процесса: {результативность алгоритма}
Если модель описывает зависимость между исходными данными и искомыми величинами, то алгоритм представляет собой последовательость действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам.
Удобной формой записи алгоритма является блок схема. Она не только достаточно наглядно описывает алгоритм, но и является основой для составления программы. Каждый класс математических моделей имеет свой метод решения, который реализуется в алгоритме. Поэтому очень важной является классификация задач по виду математической модели. При таком подходе задачи, различные по содержанию, можно решать с помощью одного и того же алгоритма. Алгоритмы задач принятия решений, как правило, настолько сложны, что без применения ЭВМ реализовать их практически невозможно.
Составление программы.
Алгоритм записывают с помощью обычных математических символов. Для того, чтобы он мог быть прочитан ЭВМ необходимо составить программу. Программа - это описание алгоритма решения задачи, заданное на языке ЭВМ. Алгоритмы и программы объединяются понятием "математическое обеспечение". В настоящее время затраты на математическое обеспечение составляют примерно полторы стоимости ЭВМ, и постоянно происходит дальнейшее относительное удорожание математического обеспечения. Уже сегодня предметом приобретения является именно математическое обеспечение, а сама ЭВМ лишь тарой, упаковкой для него.
Далеко не для каждой задачи необходимо составлять индивидуальную программу. На сегодняшний день созданы мощные современные программные средства - пакеты прикладных программ (ППП). ППП - это объединение модели, алгоритма и программы. Зачастую, к задаче можно подобрать готовый пакет, который прекрасно работает, решает многие задач, среди которых можно найти и наши. При таком подходе многие задачи будут решены достаточно быстро, ведь не надо заниматься программированием. Если нельзя использовать ППП для решения задачи без изменения его или модели, то нужно либо модель подогнать под вход ППП, либо доработать вход ППП, чтобы в него можно было ввести модель. Такую процедуру называют адаптацией. Если подходящий ППП находится в памяти ЭВМ, то работа пользователя заключается в том, чтобы ввести необходимые искомые данные и получить требуемый результат.
Ввод исходных данных.
Прежде чем ввести исходные данные в ЭВМ, их, естественно, необходимо собрать. Причем не все имеющиеся на производстве исходные данные, как это часто пытаются делать, а лишь те, которые входят в математическую модель. Следовательно, сбор исходных данных не только целесообразно, но и необходимо производить лишь после того, как будет известна математическая модель. Имея программу и вводя в ЭВМ исходные данные, мы получим решение задачи.
6) Анализ полученного решения
К сожалению достаточно часто математическое моделирование смешивают с одноразовым решением конкретной задачи с начальными, зачастую недостоверными данными. Для успешного управления сложными объектами необходимо постоянно перестраивать модель на ЭВМ, корректируя исходные данные с учетом изменившейся обстановки. Нецелесообразно тратить время и средства на составление математической модели, чтобы по ней выполнить один единственный расчет. Экономико-математическая модель является прекрасным средством получения ответов на широкий круг росов, возникающих при планировании, проектировании и в ходе производства. ЭММ может стать надежным помощником при принятии каждодневных решений, возникающих в ходе оперативного управления производством.
ИСПОЛЬЗОВАНИЕ БЛОК-СХЕМ
Физическая природа моделируемой системы может быть представлена с помощью блок-схемы. Простой пример - предыдущая блок-схема, хотя она недостаточно подробна.
Выделим основные составляющие блок схемы:
1) Прямыми линиями представлены материальные потоки, характеризующиеся определенными свойствами. Это не обязаельно должны быть потоки какого-то физического вещества; таким же образом могут быть представлены, например, потоки информации, денег. Если два материальных потока характеризуются разными свойствами и эти различия существенны для модели, то мы должны изобразить их разными линиями.
2) Прямоугольниками представлены блки предприятия и оборудование, или, в более общем случае, подсистемы, которые имеют свое определенное назначение. Характеристики потоков меняются, а блоки являются точками входа и выхода для множеств линий, представляющих потоки.
3) Принято, что общее направление движения потоков происходит слева направо. Таким образом, в блок-схеме, описывающей производственный процесс, поступающее сырье изображено стрелками входа в левой части блок-схемы, а конечные потоки - линиями, заканчивающимися справа в столбцах, ыотвечающих конечным продуктам. Такие столбцы особенно удобны, когда конечный продукт получается соединением нескольких потоков, как мы это увидим в нашем примере.