2.01 Заданы три числа: а, b, с. Определить, могут ли они быть сторонами треугольника, и если да, то определить его тип: равносторонний, равнобедренный, разносторонний. Замечание. Условия существования треугольника: сумма любых двух сторон должна быть больше третьей. Нельзя исключать экстремальных случаев, когда одна (или несколько) сторон равны нулю.
2.02. Треугольник задан длинами своих сторон: а, b, с. Определить, является ли он тупоугольным, прямоугольным или остроугольным. Замечание. Достаточно, используя теорему косинусов найти знаки косинусоввнутренних углов треугольника, не вычисляя самих углов (они могут быть нулевыми или развернутыми).
2.03.Треугольник задан координатами своих вершин на плоскости: А(ха,уа), В(хb,уb), С(хс,ус). Определить, является он прямо-, остро- или тупоугольным.
2.04.Четырехугольник ABCD задан координатами своих вершин на плоскости:: А(ха,уа), В(хb,уb), С(хс,ус), D(xd,yd). Проверить, является ли он выпуклым. Замечание. Есть несколько способов проверки выпуклости: анализ линейных неравенств, задаваемых сторонами; разбиение четырехугольника на треугольники со сравнением сумм их площадей и другие.
2.05.Четырехугольник ABCD задан координатами своих вершин на плоскости: А(ха,уа), В(хb,уb), С(хс,ус), D(xd,yd). Определить тип четырехугольника: прямоугольник, параллелограмм, трапеция, произвольный четырехугольник. Учесть погрешность вычислений.
2.06.Пройдет ли кирпич со сторонами а, b и с сквозь прямоугольное отверстие со сторонами p и q? Стороны отверстия должны быть параллельны граням кирпича.
2.07.Может ли шар радиуса r пройти через ромбообразное отверстие с диагоналями р и q?
2.08.Можно ли коробку размером a*b*c упаковать в посылку размером r*s*t? «Углом» укладывать нельзя.
2.09.Можно ли из круглой заготовки радиуса r вырезать две прямоугольные пластинки с размерами a*b и c*d?
2.10.Можно ли на прямоугольном участке застройки размером а на b метров разместить два дома размером в плане р на g и r на q метров? Дома можно располагать только параллельно сторонам участка.
2.11.Проверить, лежит ли окружность (x-а1)2 +(у-b1)2=r12 целиком внутри окружности (х-а2)2+(у-b2)2 =r22 или наоборот.
2.12.Лежит ли точка М(хт,уm) внутри треугольника, заданного координатами своих вершин А(ха,уа), В(хв,ув), С(хс,ус) на плоскости?
2.13.Два отрезка на плоскости заданы координатами своих концов. Определить, имеют ли эти
отрезки общие точки. Замечание. Необходимо рассмотреть различные случаи взаимной ориентации отрезков: на одной прямой, на параллельных или пересекающихся прямых. Тестирование должно предусмотреть все такие ситуации!
2.14.Среди заданных целых чисел k, l, т найти пары кратных.
2.15.Как известно, число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3. Проверить этот признак на примере заданного трехзначного числа. Замечание. Теоретическое утверждение о признаке делимости предлагается проверить на примере любого вводимого числа. Признак считается доказанным, но не будет лишним поиск для него контрпримеров.
2.16.Заданы координаты вершин треугольника ABC на плоскости. Вывести их в порядке обхода по часовой стрелке (для проверки достаточно рассмотреть знаки внутренних углов).
2.17.Путник двигался tl часов со скоростью v1, затем t2 часов — со скоростью v2 и t3 часов — со скоростью v3. За какое время он одолел первую половину пути, после чего запланировал привал?
2.18.Можно ехать на такси со скоростью v1 км/ч и оплатой р1 руб./км либо идти пешком со скоростью v2 км/ч бесплатно. Как с наименьшими затратами преодолеть путь s за время t, если это возможно? Каковы эти затраты? Тестирование. Рекомендуется рассмотреть «запредельные» случаи: когда времени слишком мало, чтобы успеть даже на такси, либо слишком много, так что и пешком можно с запасом успеть до отхода поезда.
2.19.Имеются три раствора полезного вещества с концентрациями р1, р2 и р3 каждый и стоимостью S1, S2 и S3 соответственно. Можно ли смешать их так, чтобы получить раствор с заданной концентрацией р наименьшей стоимости? Указание. Пусть a1, а2, а3 — долевые содержания растворов в смеси. Тогда для получения заданной концентрации р необходимо: р1а1+ р2а2+p3a3 = р. Кроме того, нужно учесть условие «комплектности» смеси: а1+а2+а3=1; а1>0; а2>0; а3>0. При этих условиях необходимо найти наименьшее значение линейной функции: S= S1a1 + S2a2 + S3a3 ® min.C учетом ограничений задача сводится к минимизации линейной функции одного переменного на отрезке, однако искомые выражения и условия получаются достаточно громоздкими. Можно показать, что в решении будут участвовать не более двух растворов. Тогда достаточно среди вариантов: а) а1=0; б) а2 = 0; в) а3=0 выбрать оптимальный, и затем провести необходимые расчеты.
2.20.Суточный рацион коровы составляет и кг сена, v кг силоса и w кг комбикорма. В хозяйстве, содержащем стадо из k голов, осталось s центнеров сена, r тонн силоса и f мешков комбикорма по 50 кг. Сколько еще дней хозяйство сможет кормить коров по полному рациону? Какой из кормов кончится раньше других?
2.21.В госуниверситете принято, что старшая цифра номера студенческой группы означает номер факультета, средняя — последнюю цифру года поступления, младшая — порядковый номер группы на курсе. Продолжительность обучения — не более 6 лет (магистратура). Дан номер группы студента и текущий год. Напечатать, в каком году он поступил и на каком факультете учится. Например, гр. 432,1996 г. факультет математический, год поступления 1993.Для справки приведены номера факультетов:
1. исторический;
2. экономический;
3. юридический;
4. математический;
5. физический;
6. химический;
7. биологический;
8. филологический;
9. географический;
10. социологический.
Тестирование. Предусмотреть невозможные ситуации, например, гр. 521, год 2001.
2.22.Банк предлагает 3 вида срочных вкладов: на 3 месяца под pl %, на 6 месяцев под р2 % и на год под р3 %. Какой из вкладов наиболее выгоден для вкладчика?
2.23.Для заданного 0 < п < 200, рассматриваемого как возраст человека, вывести фразу вида: «Мне 21 год», «Мне 32 года», «Мне 12 лет».
2.24.Из пункта А в пункт В выехал велосипедист со скоростью v0 км/час. Одновременно навстречу ему из пункта В двинулся «автостопом» другой путник. S1 м он двигался со скоростью vl м/час, S2 м — со скоростью v0 км/час, S3 м — со скоростью v3 км/час. Через сколько часов после старта и в какой точке путники встретились?
2.25.Из круга какого наименьшего радиуса можно вырезать треугольник со сторон ми а, b, с? Указание. Пусть с — большая из сторон треугольника. Если угол С — тупой, сторона с совпадает с диаметром круга, и его радиус: r = с/2. В противном случае имеем описанную окружность: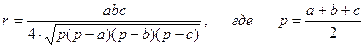 
-полупериметр треугольника.
2.26.Написать программу, которая после введенного с клавиатуры числа (в диапазоне от 1 до 999), обозначающего денежную единицу, дописывает слово "рубль" в правильной форме. Например, 12 рублей, 21 рубль и т. д.
2.27.Написать программу, которая после введенного с клавиатуры числа (в диапазоне от 1 до 99), обозначающего денежную единицу, дописывает слово "копейка" в правильной форме. Например, 5 копеек, 41 копейка и т.д.
2.28.С клавиатуры вводится сегодняшняя дата. Написать программу, которая вычисляет дату следующего дня.
2.29.Написать программу, которая вычисляет оптимальный вес для пользователя, сравнивает его с реальным и выдает рекомендацию о необходимости поправиться или похудеть. Оптимальный вес вычисляется по формуле: Рост в см - 100.
2.30.Даны действительные числа x и y, не равные друг другу. Меньшее из этих двух чисел заменить половиной их суммы, а большее - их удвоенным произведением.
2.31.Даны целые числа m, n. Если числа не равны, то заменить каждое из них одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
2.32.Услуги телефонной сети оплачиваются по следующему правилу: за разговоры до А минут в месяц оплачиваются В р., а разговоры сверх установленной нормы оплачиваются из расчета С р. в минуту. Написать программу, вычисляющую плату за пользование телефоном для введенного времени разговоров за месяц.
2.33.Даны три стороны одного и три стороны другого треугольника. Определить, будут ли эти треугольники равновеликими, т.е. имеют ли они равные площади.
2.34.Грузовой автомобиль выехал из одного города со скоростью v1 км/ч. Через t ч в этом же направлении выехал легковой автомобиль со скоростью v2 км/ч. Составить программу, определяющую, догонит ли легковой автомобиль грузовой через t1 ч после своего выезда.
2.35.Перераспределить значения переменных x и y так, чтобы в x оказалось большее из этих значений а в y - меньшее.
2.36.Определить правильность даты, введенной с клавиатуры (число - от 1 до 31, месяц - 1 до 12). Если введены некорректные данные, то сообщить об этом.
2.37.Составить программу, определяющую результат гадания на ромашке - “ любит - не любит”, взяв за исходное данное количество лепестков n.
2.38.Написать программу нахождения суммы большего и меньшего из 3 чисел.
2.39.Написать программу, распознающую по длинам сторон среди всех треугольников прямоугольные. Если таковых нет, то вычислить величину угла С.
2.40.Найти max{min(a, b), min(c, d)}.
2.41.Даны три числа а, b, с. Определить какое из них равно d. Если ни одно не равно d, то найти max (d-a, d-b, d-c).
2.42.Даны четыре точки А1(x1,y1), А2(x2,y2), A3(x3,y3), А4(x4,y4). Определить, будут ли они вершинами параллелограмма.
2.43.Даны три точки А(x1,y1), В(x2,y2), C(x3,y3). Определить будут ли они расположены на одной прямой. Если нет, то вычислить 
.
2.44.Даны действительные числа а, b, c. Удвоить эти числа, если а< b <c, и заменить их абсолютными значениями, если это не так.
2.45.На оси ОX расположены три точки а, b, c. Определить, какая из этих точек b, или с расположена ближе к а.
2.46.Даны три положительных числа a, b, c. Проверить, могут ли они быть длинами сторон треугольника. Если да, то вычислить площадь этого треугольника.
2.47.Написать программу решения уравнения ax3+bx=0 для произвольных а, b.
2.48.Дан круг радиуса R. Определить, поместится ли правильный треугольник со стороной а в этом круге.
2.49.Даны числа x, y, z. Найти значение выражения:
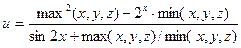
2.50.Написать программу, которая проверяет, является ли год високосным.
2.51.Даны числа c и b - длины катетов одного прямоугольного треугольника, a c и d - другого. Будут ли эти треугольники подобными.
2.52.Составить программу, проверяющую будет ли сумма двух первых цифр заданного четырёхзначного числа равна сумме двух его последних.
2.53.Составить программу, проверяющую будет ли сумма цифр данного трёхзначного числа N являться чётным числом.
2.54.Составить программу, проверяющую будет ли точка с координатами (х,у) принадлежать части плоскости, лежащей между прямыми х=m, x=n (m<n).
2.55.Составить программу, проверяющую будет ли квадрат заданного трехзначного числа равен кубу сумме цифр этого числа.
2.56.Составить программу, проверяющую будет ли целое число N являться чётным двухзначным числом.
2.57.Проверить будет ли данная тройка натуральных чисел a, b, c являться тройкой Пифагора, т.е. c2=a2+b2.
2.58.Написать программу, которая проверяла бы истинность высказывания: все цифры данного четырёхзначного числа N различны.
2.59.Написать программу проверяющую будут ли цифры данного четырёхзначного числа N образовывать строго возрастающую последовательность.
2.60.Написать программу проверяющую будут ли цифры данного трёхзначного числа N являться членами арифметической прогрессии.
2.61.Написать программу проверяющую будут ли цифры данного трехзначного числа N являться членами геометрической прогрессии.
2.62.Написать программу проверяющую будут ли данные числа c и d являться соответственно квадратом и кубом числа а.
2.63.Написать программу проверяющую будет ли цифра М входить в десятичную запись четырёхзначного числа N.
2.64.Написать программу проверяющую будет ли данное четырёхзначное число читаться одинаково слева направо и справа налево.
2.65.Написать программу проверяющую будет ли произведение натуральных чисел а и b кратно числу с.
2.66.Написать программу проверяющую будет ли сумма двух действительных чисел а и b являться целым числом, т.е. будет ли дробная часть суммы равна нулю.
2.67.Написать программу проверяющую будет ли данное натуральное число а кратно числу b, но не кратно числу с.
2.68.Определить, принадлежит ли число диапазону и равно ли оно одной из границ. Если число принадлежит диапазону, то заменить его удвоенным значением. Число и границы ввести с клавиатуры. Вывести соответствующие сообщения на экран.
2.69.Даны два действительных числа. Арифметические действия пронумерованы: 1-сложение, 2 – вычитание, 3- умножение, 4 – деление. Составить программу, которая бы в зависимости от введенного знака операции выполняла бы соответствующее действие над числами. При делении проверять делитель, если он равен 0, выдать сообщение «На 0 делить нельзя».
2.70.Даны две дроби a/b и c/d. Если они правильные, то сравнить дроби.
2.71. Написать программу вычисления стоимости покупки с учетом скидки. Скидка s% предоставляется, если сумма покупки превышает M руб. и p %, если сумма покупки больше N руб (s<p, M<N).
2.72.Написать программу решения квадратного уравнения. Программа должна проверять правильность исходных данных и в случае, если коэффициент при второй степени неизвестного равен нулю, выводить соответствующее сообщение.
2.73.Написать программу вычисления сопротивления электрической цепи, состоящей из двух сопротивлений. Сопротивления могут быть соединены последовательно или параллельно.
2.74.Напишите программу, которая запрашивает у пользователя номер месяца и затем выводит соответствующее название времени года. В случае, если пользователь введет недопустимое число, программа должна вывести сообщение «Ошибка ввода данных».
2.75.Написать программу проверки знания даты начала второй мировой войны. Программа должна вывести вопрос и три варианта ответа. Пользователь должен выбрать правильный ответ и ввести его номер. В случае неправильного ответа пользователя, программа должна выводить правильный ответ.
2.76.Написать программу, которая бы по введенному номеру единицы измерения (1 - дециметр, 2 - километр, 3 - метр, 4 - миллиметр, 5 - сантиметр) и длине отрезка L выдавала бы соответствующее значение длинны отрезка в метрах.
2.77.Имеется пронумерованный список деталей: 1 - шуруп, 2 - гайка, 3 - винт, 4 - гвоздь, 5 - болт. Составить программу, которая по номеру детали выводит на экран ее название.
2.78.Пусть элементами прямоугольного равнобедренного треугольника являются:
š катет a;
š гипотенуза b;
š высота, опущенная из вершины прямого угла на гипотенузу h;
š площадь S;
Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника.
2.79.Написать программу, которая бы по введенной букве (первая буква сезона з - зима, в - весна, л - лето, о - осень) выдавала соответствующие этому времени года месяцы.
2.80.Даны три угла. Проверить могут ли они быть углами треугольника, если да, то проверить будет ли этот треугольник остроугольным.
2.81.Написать программу, которая запрашивает у пользователя номер дня недели и выводит одно из сообщений: "Рабочий день", "Суббота" или "Воскресенье".
2.82.Даны две стороны треугольника и противолежащие им углы. Проверить будет ли существовать треугольник с такими углами, если да, то проверить является ли он прямоугольным. В случае положительного ответа вывести на экран длину гипотенузы.
2.83.Напишите программу, которая запрашивает у пользователя номер месяца и затем выводит соответствующее название времени года. В случае, если пользователь введет недопустимое число, программа должна вывести сообщение "Ошибка ввода данных".
2.84.Даны действительные числа a, b, c (a>0). Полностью исследовать биквадратное уравнение ax4+bx2+c=0, то есть, если действительных корней нет, то выдать об этом сообщение, иначе найти все действительные корни, сообщив при этом, сколько их них являются различными.
2.85.Написать программу вычисления стоимости разговора по телефону с учетом 20% скидки, предоставляемой по субботам и воскресеньям.
2.86.Билеты в кинотеатр стоят: с 1 по 10 ряд - 3 р., с 11 по 15 ряд – 2 р.45 к., с 16 по 20 ряд – 2 р. Количество билетов и ряд ввести с клавиатуры. Вывести на экран стоимость билетов, ввести сумму денег и вывести на экран сдачу либо сообщение что денег не хватает.
2.87.Даны числа N, и предполагаемый делитель k (0<k<N/2). Проверить будет ли введенное число N двузначным, если да, то будет ли оно кратно k. Выводить на экран соответствующие сообщения.
2.88.Своими координатами заданы точки А и В на оси абсцисс. Проверить будет ли точка С(х1, у1) находиться между точками А и В. Если да, то найти к какой из них точка С находится ближе.
2.89.Написать программу, вычисляющую и выдающую на экран значение функции F(x) для любых значений х:
x/2 + (x/5)2 , при х < -10
F(x) = (x+1)2 + 3(x+1)/4, при -10 < x < 10
x2/2 + 5x –2, при x > 10
2.90.Пусть элементами круга являются радиус (первый элемент), диаметр (второй элемент), и длина окружности (третий элемент). Составить программу, которая по номеру элемента запрашивала бы его соответствующее значение и вычисляла бы площадь круга.
2.91.Написать программу, которая выводит пример на вычитание (в пределах 100), запрашивает ответ пользователя, проверяет его и выводит сообщение "Правильно!" или "Вы ошиблись" и правильный результат.
2.92.Определить, имеется ли среди чисел а, b, с хотя бы одна пара взаимно противоположных чисел, если имеется то вывести эти числа, а затем вывести сумму абсолютных значений этих чисел.
2.93.Написать программу, которая бы по введенному номеру единицы измерения (1 - миллиграмм, 2 - грамм, 3 - центнер, 4 - тонна) и массе тела m выдавала бы соответствующее значение в системе СИ.
2.94.Для данного аргумента х вычислить значение функции:
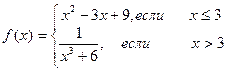
2.95.С клавиатуры вводят знаки двух электрических зарядов. Написать программу выводящую сообщение о взаимодействии этих зарядов (заряды отталкиваются или заряды притягиваются).
2.96.Написать программу-тест: на экране появляются по очереди три вопроса (на любую тему, по усмотрению программиста) и варианты ответов на них. В конце работы программа выдает количество баллов, заработанных тестируемым, по результатам ответа.
2.97.Найти площадь треугольника по заданным двум сторонам и углу между ними. Предоставить возможность ввода угла в радианах или в градусах. Замечание: функция sin, встроенная в среду программирования СИ работает только с радианной мерой угла.
2.98.Дан радиус сферы. По выбору пользователя выводить на экран значение площади поверхности сферы или объема сферы.
2.99.Даны два числа. Найти их наименьший общий делитель.
2.100. Найти порядковый номер максимальной и минимальной цифры в четырехзначном числе.