Значений из функции).
6.01 Написать функцию, которая вычисляет объем цилиндра. Параметрами функции должны быть радиус и высота цилиндра.
6.02 Написать функцию, которая возвращает максимальное из двух целых чисел, полученных в качестве аргумента.
6.03 Написать функцию, которая сравнивает два целых числа и возвращает результат сравнения в виде одного из знаков: >, <, =.
6.04 Написать функцию, которая вычисляет сопротивление цепи, состоящей из двух резисторов. Параметрами функции являются величины сопротивлений и тип соединения (последовательное или параллельное). Функция должна проверять корректность параметров: если неверно указан тип соединения, то функция должна возвращать –1.
6.05 Написать функцию, которая вычисляет значение ab. Числа a и b могут быть любыми дробными положительными числами.
6.06 Написать функцию, которая находит определитель матрицы 3*3.
6.07 Написать функцию Prosent, которая возвращает процент от полученного в качестве аргумента числа.
6.08 Найти площадь треугольника, заданного координатами своих вершин, определив функцию для расчета длины отрезка по координатам его вершин.
6.09 Написать функцию, которая решает систему линейных уравнений, коэффициенты которых вводятся с клавиатуры.
6.10 Написать функцию «Факториал» и программу, использующую эту функцию для вывода таблицы факториалов.
6.11 Написать функцию Dohod, которая вычисляет доход по вкладу. Исходными данными для функции являются: величина вклада, процентная ставка (годовых) и срок вклада (количество дней).
6.12 Написать функцию glasn, которая возвращает 1, если символ, полученный функцией в качестве аргумента, является гласной буквой русского алфавита, о ноль – в противном случае.
6.13 Написать функцию, обеспечивающую решение квадратного уравнения, Параметрами функции должны быть коэффициенты и корни уравнения. Значение, возвращаемое функцией, должно передавать в вызывающую программу и информацию о наличии у уравнения корней: 2 – два разных корня, 1 – корни одинаковые, 0 – уравнение не имеет решения. если исходные данные не верные, то функция должна возвращать –1.
6.14 Написать функцию, которая выводит строку, состоящую из одинаковых символов. Длина строки и символа являются параметрами процедуры.
6.15 Написать функцию, которая вычисляет объем и площадь параллелепипеда.
6.16 Написать функцию frame, которая выводит на экран рамку. В качестве параметров функции должны передаваться координаты левого верхнего угла и размер рамки.
6.17 Найти периметр треугольника, заданного координатами своих вершин, определив функцию для расчета длины отрезка по координатам его вершин.
6.18 Найти все трехзначные простые числа, определив функцию, позволяющую распознавать простые числа.
6.19 Написать программу вычисления суммы факториалов всех нечетных чисел от 1 до 9, использовав функцию вычисления факториала.
6.20 Даны основания и высоты двух равнобедренных трапеций. Найти сумму их периметров, определив функции периметра равнобедренной трапеции по ее основаниям и высоте.
6.21 Даны шесть различных чисел. Найти максимальное из них, определив функцию, находящую максимум двух различных чисел.
6.22 Даны два натуральных числа. Выяснить в каком из них больше цифр, определив функцию для расчета количества цифр натурального числа.
6.23 Сколькими способами можно отобрать команду в составе 5 человек из 8 кандидатов, из 10 кандидатов, из 11 кандидатов? Вычисления оформить в виде функции.

6.24 В порт в среднем заходит 3 корабля в день. Какова вероятность того, что в порт придет 2 корабля; 4 корабля? Вычисления оформить в виде функции.

6.25 Два спортсмена начинают одновременно движение из одной точки. Первый начинает движение со скоростью 10 км/час и равномерно увеличивает скорость на 1 км за каждый час. Второй начинает движение со скоростью 9 км/час и равномерно увеличивает скорость на 1,6 км за каждый час. Выяснить какой из спортсменов преодолеет больший путь через 1 час, 4 часа. Вычисления путей оформить в виде функции.
6.26 Два спортсмена начинают одновременно движение из одной точки. Первый начинает движение со скоростью 10 км/час и равномерно увеличивает скорость на 1 км за каждый час. Второй начинает движение со скоростью 9 км/час и равномерно увеличивает скорость на 1,6 км за каждый час. Определить, когда 2-й спортсмен догонит первого. Вычисления оформить в виде функции.
6.27 В партии из K изделий имеется L дефектных. Для контроля выбираются R изделий. Определить вероятность того, что S изделий будут дефектными. Решить задачу для K=10, L=5, R=4, S=2; и K=10, L=4, R=5, S=3. Вычисления оформить в виде функции. 
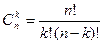
6.28 Два треугольника заданы координатами своих вершин A, B, C. Вычислить площади треугольников с помощью формулы Герона и определить какой из них имеет большую площадь. Данные для первого треугольника: A(1;1), B(4;2), C(2;3,5). Для второго треугольника: A(1;2), B(4;1), C(3;3,5). Вычисления оформить в виде функции. 

6.29 Футболист ударом ноги посылает мяч вертикально вверх с высоты 1м и с начальной скоростью 20м/сек. На какой высоте мяч будет через 1 с, 3 с. Вычисления оформить в виде функции.
6.30 Два простых числа называются «близнецами», если они отличаются друг от друга на 2 (например числа 41 и 43). Напечатать все пары чисел-близнецов, не превышающих 200.
6.31 Найти все трехзначные простые числа, определив функцию, позволяющую распознавать простые числа.
6.32 Дата некоторого дня характеризуется тремя натуральными числами: g (год), m (порядковый номер месяца), n (число). По заданным g, m, и n вычислить дату предыдущего дня и дату следующего дня, определив функцию, вычисляющую количество дней в том или ином месяце. Учесть случаи, когда год не является високосным и может быть високосным.
6.33 Даны натуральные числа a и b. Найти их наименьшее общее кратное, определив функцию для расчета наибольшего общего делителя двух натуральных чисел, используя алгоритм Евклида.
6.34 Круг задан координатами центра Q и координатами одной из точек окружности (точка Z). Внутри круга содержится квадрат, заданный координатами трех своих вершин А, В, С. Произвольно выбирается точка внутри круга. Найти вероятность того, что эта точка попадет в квадрат. Задачу решить для Q(4,5), Z(7,5), A(2,4), B(4,6),C(2,6) и для Q(5,4), Z(5,7), A(5,3), B(3,5;4,5),C(5,6). Вычисления оформить в виде функции.
Искомая вероятность равна 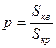 .
.
6.35 Футболист ударом ноги посылает мяч вертикально вверх с высоты 2м и с начальной скоростью 30м/сек. Определить, когда мяч будет на высоте 5м, 10м. Вычисления оформить в виде функции.
6.36 Определить вероятности того, что среди 5 детей одной семьи нет ни одной девочки, две девочки, три девочки, четыре девочки, 5 девочек. Вероятность рождения девочки и мальчика одинакова (р=0,5, q=1-p).  (из n детей m девочек). Вычисления оформить в виде функции.
(из n детей m девочек). Вычисления оформить в виде функции.


6.37 Футболист ударом ноги посылает мяч вертикально вверх, с высоты 1м и с начальной скоростью 25м/сек. Определить с точностью до 0,35 сек, когда и на какой максимальной высоте окажется мяч в течение 4 с. Вычисления оформить в виде функции.
6.38 Круг задан координатами центра Q и координатами одной из точек окружности (точка Z). Внутри круга содержится треугольник, заданный координатами своих вершин А, В, С. Произвольно выбирается точка внутри круга. Найти вероятность того, что эта точка попадет в треугольник. Задачу решить для Q(4,5), Z(7,5), A(2,4), B(5,5),C(3,6) и для Q(5,4), Z(5,7), A(3,3), B(7,5),C(5,6). Вычисления оформить в виде функции.
Искомая вероятность равна  .
.
6.39 Футболист ударом ноги посылает мяч вертикально вверх с высоты 2м и начальной скоростью 30м/сек. Определить с точностью до 0,15 с, когда и на какой высоте будет максимальная скорость мяча в течение 7 с. Вычисления оформить в виде функции.
6.40 Два спортсмена начинают движение из одной точки. Первый начинает движение со скоростью 10 км/час и равномерно увеличивает скорость на 1 км за каждый час. Второй начинает движение со скоростью 9 км/час и равномерно увеличивает скорость на 1,6 км за каждый час. Определить с точность до 0,25 часа, когда и каким окажется максимальное расстояние между спортсменами в течение 5 часов. Вычисления оформить в виде функции.
6.41 Стрелок производит по мишени 5 выстрелов. Вероятность попадания в мишень при каждом выстреле 0,6. Вычислить вероятность попадания в мишень: ни разу, 1 раз, 2 раза, 3 раза, 4 раза, 5 раз. Определить когда будет максимальная вероятность. Вычисления оформить в виде функции.


6.42 Составить программу для нахождения числа, которое образуется из данного натурального числа при записи его цифр в обратном порядке, используя функцию.
6.43 Дано натуральное число N. Составить программу формирования массива, элементы которого являются цифры числа N, используя функцию.
6.44 Найти все простые числа, не превосходящие n, используя функцию для определения, является ли число палиндромом
6.45 Дано четное число n>2. Используя функцию, проверить для него гипотезу Гольдбаха: каждое четное n представляется в виде суммы двух простых чисел.
6.46
Литература
1. М. Уэйт, С. Прайт, Д. Мартин. Язык СИ. - М.:"Мир", 1988 г.
2. Кеpниган Б., Ритчи Д. "Язык пpогpаммиpования Си.", - М.:Финансы и статистика, 1992г.
3. Подбельский В.В., Фомин С.С. Программирование на языке СИ. – М.:Фининсы и
статистика, 1998г.
4. Подбельский В.В. Программирование на языке С++. – М.:Фининсы и статистика, 2001г.