Общая тенденция при решении такого рода задач— это сразу же начать обдумывать возможные улучшения существующего решения (если, оно, конечно, есть). В нашей задаче напрашивается начать с тщательного исследования решения, приведенного на рис. 6-2, и искать улучшения, которые сделают процесс более экономичным. Инженер, решающий эту задачу, сразу же начнет интересоваться различным оборудованием для укладки, взвешивания и зашивания мешков, новыми приспособлениями, облегчающими труд, лучшими способами перевозки тяжелых мешков, объединением нескольких операций в одну и др. Но это как раз то, чего не нужно делать при знакомстве с задачей, так как такой подход только усложнит процесс нахождения решения. Однако вся эта деятельность принесет большую пользу на дальнейших этапах. Поступая описанным образом, инженер вырабатывает решение задачи, которую ему не удалось определить. Та«ая практика едва ли приемлема для нахождения эффективного решения задачи. Кроме того, не определив задачу, инженер может искать решение вовсе не той задачи или же его решение будет плохим.
Вспомним, что формулирование задачи — это общий обзор, без углубления в детали. Основная цель его — определение состояний А - я В. Важно,.чтобы инженер выполнил такое определение в самом начале и чтобы на этом этапе он не задумывался ни о каких возможных решениях. Вот несколько различных формулировок задачи:
1. Найти наиболее экономичный способ взвешивания, наполнения, сшивания и укладки мешков с кормами.
2. Найти наиболее экономичный метод перехода от бункера-смесителя (состояние А) к штабелю мешков в товарном складе (состояние В).
3. Найти наиболее экономичный метод перехода от бункера-смесителя к мешкам нагруженным на грузовик.
\091\
4. Найти наиболее экономичный способ перехода от бункера-смесителя к грузовику.
5. Найти наиболее экономичный метод перехода от бункера-смесителя к вывозящему транспорту.
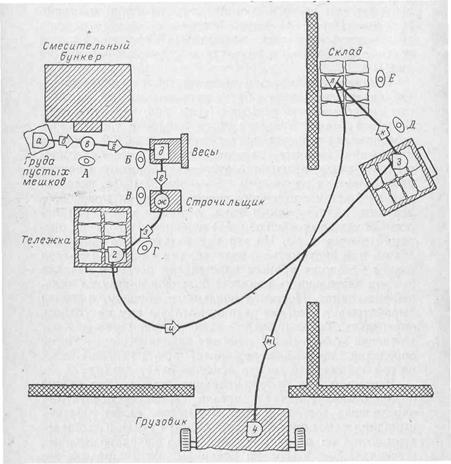
Рис. 6-2. Существующий метод наполнения, хранения и погрузки мешков с кормами.
а —сложенные в груду мешки ждут наполнения; б — человек А берёт пустой мешок и подставляет его под край желоба для наполнения; в — человек Л насыпает в мешок 40 кг кормов, вручную управляя скоростью засыпки; г — человек Л передает мешок человеку Б; д — человек Б проверяет вес и добавляет или же отсыпает корма, чтобы вес мешка был приблизительно 40 кг; е — человек Б передает мешок человеку В; ж— человек В загибает и застрачивает верх мешка; з — человек Г берет мешок и грузит его на тележку; и — нагруженная тележка буксируется к складу; к — мешки складываются в штабель людьми Д и Е; л —мешки на складе, м — мешки нагружены на грузе» вик для доставки заказчику*
\092\
6. Найти наиболее экономичный метод перехода от бункера-смесителя к хранилищу потребителя.
7. Найти наиболее экономичный метод перехода от хранилища корма к хранилищу потребителя.
8. Найти наиболее экономичный способ перехода кормов от производства >к потребителю.
Формулировка 1 неудовлетворительна, так «ак с ее помощью не удается определить состояния А и В. Кроме того, она содержит ограничения «наполнение, взвешивание, сшивание и укладка», которым не место в формулировке задачи. Заметьте, что эти ограничения не что иное как частные характеристики существующего решения задачи. Частая ошибка в определении задачи — неоправданное принятие инженером некоторых характеристик имеющегося решения, присутствие которых он считает необходимым в новом решении. В результате инженер отрезает себе дорогу ко многим решениям, которые при других обстоятельствах можно было бы с пользой применить. Преодолеть эту тенденцию — первейшая задача молодого инженера.
Формулировки 2 и 8 можно принять, так как они определяют состояния А и В; они не имеют никаких ограничений и почти свободны от ненужных деталей. Однако они неравноценны. Такое большое число формулировок и различные результаты, достигаемые при их реализации, заставляют нас обратиться к тому, что называют «широтой формулировки задачи».
Широта формулировки задачи
В формулировках 2 и 3 принято, что в состоянии В корма должны быть в мешках. В формулировке 4 оговорен только грузовик, что позволяет использовать любую другую тару или не пользоваться ею вовсе. В формулировке 5 оговорен только вывозящий транспорт, что открывает дополнительные возможности по применению различных видов транспорта. Это исключение специфических деталей состояний А и В продолжается до тех пор, пака не останутся только производитель и потребитель. Благодаря этому перед инженером открываются широкие возможности по применению различных методов управления, способов транспортировки, упаковки, • типов и размеров тары и т. д. Из приведенных примеров очевидно, что чем шире сформулированы состояния А и
\093\
В, тем больше может быть у инженера разнообразных решений. Инженер должен стараться сделать свою формулировку настолько общей, насколько позволяет важность задачи. Нарушение этого правила может быть причиной того, что целая область выгодных решений

Рис. 6-3. Различные формулировки задачи о распределении кормов, иллюстрирующие постепенное расширение формулировки задачи.
будет исключена из рассмотрения. Так, инженер, не раздумывая, принявший за состояние В штабель мешков на складе, так и закончит процесс проектирования, не сознавая, что он сам себя «обокрал».
В формулировке 2 состояние В — это штабель на складе, как показано на рис. 6-3. В формулировке 3 состояние В простирается до грузовика, а в формулировке 6—до потребителя. В формулировках 7 и 8 состояние А —"Протяженное. В обоих случаях задача сформулирована гораздо шире, чем в предыдущих. В общем, инженер должен стараться так широко сформулировать свою задачу, как позволяют экономика и организация производства. Чем больше общая задача подразделена на независимые частные, тем меньше эффективность общего решения. Если погрузка кормов считается одной задачей, перевозка и хранение—другой, перевозка к потребителю — третьей и разгрузка у потребителя -— четвертой, то система в общем будет далека от оптимума. Широкий же подход к задаче гораздо чаще поз-
\094\
воляет достичь оптимального решения и ценой гораздо меньших затрат.
То, как подробно определены состояния Л и В задачи, и то, как они общи, будем называть широтой формулировки задачи.
Важность широкой формулировки задачи
Если инженер, решающий задачу, описанную в предыдущем разделе, сумеет освободиться от ограничений, связанных с применением мешков, то возникнет проблема обращения с кормом внавал. Если ему удастся хорошо сформулировать задачу доставки груза потребителю, он встанет перед проблемой возможности транспортировки сыпучего корма прямо в хранилище заказчика. Очевидно, кто-то уже преуспел здесь, так как после многих лет усовершенствований методов доставки люди сейчас поставляют корма, подавая их под давлением через специальный рукав прямо в хранилище заказчика. Никаких емкостей не требуется; процесс -быстр и малотрудоемок.
Одним из наиболее важных достижений инженеров является более широкое рассмотрение задачи, чем раньше, когда задача рассматривалась по частям. Значительные нововведения в военной технике последних лет и в системах гражданской связи, информации и транспортировки являются главным образом следствием широкой постановки задач. Перед инженерами, которые смотрят на задачу шире, чем обычно, открываются огромные возможности.
Представим себе для примера некоторый город X, который подобно многим большим городам стоит перед проблемой стоянки транспорта в деловой части города. Площадь, необходимая для стоянки, составляет 40% площади Города. Такое положение заставило «отцов» города обратиться к инженерам с просьбой разработать устройство для стоянки 600 автомобилей, которое будет одной из составных частей общей стоянки, решающей проблему.
Перед тем как разбираться в деталях проектируемого устройства, инженер подумал о конструкциях, которые могут быть решением задачи. (Заметьте, что «отцы» города уже дали инженеру решение задачи!) Его задача как консультанта состоит ib том, чтобы опреде-
\095\
лить детали решения, с тем чтобы они подходили конструктивно, экономически и функционально. Инженер не рассматривает эту задачу, как средство перевозки большого числа людей из дома к месту работы и обратно. Между такой постановкой проблемы и задачей, поставленной перед нашим консультантом, большая разница. Такая широкая постановка задачи открывает перед инженером широкую область многообещающих решений. Одним из них является крупная высокоскоростная транспортная система. И, конечно, ничто в этом инженерном определении не устраняет возможности строительства города совершенно другого типа, исключающего или сокращающего необходимость в массовых перевозках пассажиров. Эта городская дилемма возникла несколько лет назад из-за недальновидности тех, кто решает Проблемы города. Тогда они посоветовали строить сеть высокоскоростных магистралей, позволяющих легко и быстро добраться на автомобиле с окраин в деловой центр. Результат этого легко можно было предсказать. Вскоре многие владельцы сезонных билетов на транспорт воспользовались преимуществом автострад и наводнили своими автомобилями коммерческие районы. Решая поставленную задачу, инженер коснулся и этической стороны дела. Он сообщил властям, что, по его мнению, увеличение площадей под стоянки для автомобилей вовсе не очевидное решение проблемы и что он не желал бы проектировать предложенное оборудование. Он высказал свою оценку этой проблемы и предложил несколько главных вариантов решения, основанных на его точке зрения. Отличительной чертой настоящего инженера является выбор решения, основанного на широком рассмотрении проблемы и умении настоять на принятом решении, если оно отвечает интересам заказчика.
Насколько широко может инженер формулировать задачу?
Решить этот вопрос — дело самого инженера. Формулировка задачи — это выражение его точки зрения и способ, с помощью которого он постигает задачу. Формулировка может состоять из нескольких мыслей или беглых замечаний, не обязательных и не категоричных. При необходимости инженер может и должен формули-
\096\
ровать задачу широко: в этом его право и преимущество. Он подведет себя и своего заказчика, если поступит иначе. Однако широкая формулировка «в уме» — это одно, а как широко инженер сумеет применить ее в процессе проектирования — это совсем другое. Реализация этой широкой формулировки часто приводит к конфликту между инженером и заказчиком.
Инженер, которому поручено решить задачу о. распределении кормов, может, например, встретить трудности, когда попытается реализовать свою широкую формулировку (изготовитель — потребитель), хотя реализовать ее — в интересах предприятия. В конце концов ему придется убеждать людей, ответственных за принятие решения, отказаться от мешков или внести изменения в методы хранения, торговую политику и пр. Некоторые люди будут сопротивляться попыткам инженера реализовать свою формулировку и будут заставлять его принять более узкое решение.
Различные способы формулировать задачу
Задачу можно удовлетворительно сформулировать словесно или схематически. Во многих случаях вполне достаточно словесной формулировки, как показано на стр. 91. Задачу можно также сформулировать с помощью простой схемы, как показано на стр. 8. Метод формулирования задачи с помощью «черного ящика», описанный в гл. 1, схематичен. Пользу такого метода можно проиллюстрировать, применив его к задаче обработки информации, которую часто решают неудовлетворительно.
Учреждение, занимающееся бронированием мест, например, в самолете или театре, является системой обработки информации. Будущий пассажир или зритель приходит в кассу и называет нужное ему время, число мест и т. д. Это — входные данные системы, показанной на рис. 6-4. Выходом тоже является информация, подтверждающая требования заказчика или же предлагающая ему другие варианты. Решение задачи происходит в «черном ящике», содержимое которого нам неизвестно или не представляет интереса. Он заменяет те детали, которых мы стараемся избежать на этом этапе проектирования, и в этом заключается польза «черного ящика». Представлять так процесс обработки информа-
\097\

Рис. 6-4. Формулировка знакомой нам задачи обработки информации с помощью «черного ящика».
ции или любую другую задачу — очень удобно. Такой способ делает задачу яснее и помогает разработчику отойти от готовых решений. Простота такого подхода может, однако, создать неверное представление об его эффективности при решении задач.
Ловушки в начале процесса проектирования
Нечасто инженеру приходится задумываться о ловушках на его пути. Он должен определить, что же действительно представляет собой задача. Сделать это часто бывает трудно, так как существо задачи скрыто за большим количеством не относящейся к делу информации, применяемыми решениями, сбивающими с толку, и бесполезными мнениями. Этому не способствует и то, что в колледжах перед студентами ставят задачи в нереально чистом виде, и студенты не привыкают и не имеют опыта распознавания задач. Описанные две ситуации заставят инженера особенно наглядно увидеть эти ловушки. Одну из них часто называют фиктивной задачей, т. е. задачей, в решении которой нет нужды. Инженер, который разрабатывает часть грузовика, в которой нет необходимости, или проектирует производственную операцию, которая может быть полностью исключена, решает фиктивную задачу. Ошибка в определении задачи, являющемся первым шагом к ее решению, приводит к плачевным результатам.
Другая распространенная ловушка возникает из-за тенденции путать задачу с решением. Общепринятое решение задачи -и это не сама задача. Если это положение кажется очевидным,.почему же мы тогда часто критикуем решение, вместо того чтобы критиковать задачу? Мы очень легко попадаем в эту ловушку, и то, как важно избежать ее, трудно переоценить. Действительно, ворчание
\098\
по поводу общепринятого решения, его неэффективности и несоответствия требованиям не имеют ничего общего с определением задачи и нахождением наилучшего решения в процессе проектирования.
Выводы
В самом начале при подходе к задаче инженеру следует тщательно сформулировать ее и убедиться: 1) что задача достойна внимания; 2) что рассмотрел он её всесторонне; 3) что он избежал деталей и 4) что он не попал под влияние имеющихся решений.
Любую задачу можно сформулировать с различной степенью широты. Инженеру следует формулировать задачу так широко, как позволяют обстоятельства.
Отход от традиционного узкого рассмотрения задача часто неожиданно приводит к значительному улучшению решения.
Что же касается ловушек и препятствий, то будущим инженерам надлежит набраться опыта в формулировании реальных задач.
Когда задача сформулирована, первая и очень важная часть определения задачи достигнута.
Упражнения
1. Определите состояния Л и В, а если необходимо, сделайте предположения для задач, стоящих перед лицами следующих профессий:
а) разносчик газет;
б) альпинист;
в) повар;
г) пожарный;
д) учитель;
е) мастер то ремонту телевизоров;
ж) гончар.
2. Опишите критерии, которые должны быть использованы в каждой из перечисленных задач.
3. Ниже приведены решения некоторых задач..Попробуйте сформулировать эти задачи:
а) общественная адресная система;
б) электрический утюг;
в) кондиционер воздуха;
г) телефонная система;
д) международный нефтепровод;
е) бутылочный завод;
ж) аэропорт;
з) очистка нефти;
и) снегоочиститель.
\099\
Глава седьмая. ПРОЦЕСС ПРОЕКТИРОВАНИЯ. АНАЛИЗ ЗАДАЧИ
Задача о стиральной машине
Фирма-изготовитель бытовых приборов предложила выпустить новый тип автоматической стиральной машины. Дирекция фирмы решила, что эта машина, помимо обычных операций стирки, будет также работать как домашняя химчистка. Был принят также ряд других решений, касающихся характеристик этой двухцелевой маши-

Рис. 7-1. Как анализирует задачу инженер, разрабатывающий стиральную машину общего назначения.
ны. Среди них следующие:
1. Устройство должно быть не более 75 см в ширину, 95 см в высоту и 75 см в.глубину.
2. Оно должно работать от сети переменного тока напряжением 115 в и частотой 60 гц.
3. Оно должно быть одо брено лабораториями страховых компаний.
4. Стоимость производства не должна превышать 125 долл.
5. Устройство должно удовлетворительно обрабатывать все виды натуральных и синтетических тканей.
После долгих консультаций с руководством и представителями торговли, хорошо знающими вкусы потребителей, а также после многих исследований и отбора инженер, которому поручили разработать эту двухцелевую
\100\
машину, анализировал задачу так, как показано на рис. 7-1. Этот анализ, обсуждаемый на последующих страницах,— Образец, рекомендуемый для анализа всех инженерных задач.
Определение состояний А и В
Согласно формулировке задачи состояние А можно определить, как некоторое количество загрязненных вещей, а состояние В — как те же вещи, очищенные от грязи. Однако для того чтобы удовлетворительно решить поставленную задачу, необходимо знать значительно больше о входе и выходе. Обор этой информации — главное в анализе задачи. На этом этапе проектирования определяются все относящиеся к делу качественные и количественные характеристики состояний Л и В. Такая спецификация входа и выхода для этой задачи показана на рис. 7-1.
Вариации входа и выхода. Только несколько характеристик входа и выхода остаются неизменными при работе машины в течение долгого времени. Следующие друг за другом загрузки изменяются по весу от нуля до 6,5кг, изменяются сами вещи и содержание влаги в них. Это динамические характеристики состояний А и В. (Динамическими характеристиками входа сталеплавильного предприятия, например, являются размеры кусков и химический состав поступающих партий руды.) Существуют средние скорость и мощность автомобильного двигателя, но эти выходные данные, конечно же, изменяются. Число автомобилей, проходящих по шоссе, изменяется по закону случайных величин, но имеет, однако, максимальное значение (пик). Точно так же вход и выход значительно изменяются в задачах об аэровокзале, системе связи и электростанции. Прежде чем решать задачу, инженер должен располагать надежной информацией об ожидаемых вариациях входа и выхода,
Определение ограничений
Другая важная функция анализа задачи состоит в определении ограничений решения. Если вход и выход определены, как грязная и чистая одежда, то это автоматически определяет неизбежную характеристику всех «приемлемых решений — они должны удалять грязь. Этот
\101\
тип ограничений, возникающий при установлении состояний А и В, обычно может быть выделен дедуктивно. Существует, конечно, и другой тип ограничений — ограничения, установленные дирекцией (сверху). Примерами таких ограничений являются ограничения 2 — 6 на рис. 7-1. Инженер обычно изучает ограничения такого типа через контакты с исполнителями, потребителями, заказчиками и пр., а также собирая различные -факты (например, определяя, каковы ограничения при домашнем применении).

Рис. 7-2. Задача с тремя переменными решения, каждая из которых имеет ограничения, изображенная в трехмерном пространстве.
Переменные решения и пространство решения. В процессе проектирования.возможные решения зависят от различных факторов. Решение задачи о стиральной машине может быть различным в смысле размеров, формы, веса, типа механизма, применяемых материалов и др. Величины, в зависимости от которых может изменяться решение определенной задачи, будем называть переменными решения. Окончательно решение задачи состоит ич определенных значений каждой переменной, например размера, веса, формы и пр. Иными словами, решение можно рассматривать как функцию N переменных в N-мерном пространстве. Для задачи с тремя переменными: x, у и z решение имеет три измерения, как показано на рис. 7-2. Значения некоторых переменных могут быть ограничены, например размеры и стоимость производства стиральной машины. Это означает, что существуют границы -многомерного пространства, определяющие область, внутри которой инженер должен выбрать окончательное решение. Это пространство называют областью приемлемых решений. Пусть в задаче с тремя
\102\
переменными х не должен быть больше а, у не должен превышать и, a z не больше с. Тогда область приемлемых решений будет иметь вид, показанный на рис. 7-2. Решения задачи должны быть внутри этой области. Значения a, b и с — ограничения решения.
Некоторые переменные решения устанавливаются заранее и не могут быть изменены инженером. Например, в случае стиральной машины питание установлено 115 в, 60 гц. Другие переменные можно менять, но только внутри некоторых пределов; например, высота прибора не должна быть больше 95 см.
Ограничения, которые инженер не может принять. Можно разработать стиральную машину, которая будет обрабатывать все виды тканей, но затраты на ее разработку и производство будут высоки. Инженер знает, что себестоимость такой машины будет много выше себестоимости машины, обрабатывающей почти все ткани. Он убежден, что создание машины, стирающей все виды тканей, экономически нецелесообразно. Учитывая эти обстоятельства, инженер должен решить, принять это ограничение (обработка всех видов тканей) или попытаться убедить руководство отменить первоначал --но принятое решение.
Более того, инженеру ясно, что два из налагаемых ограничений несовместимы. Стоимость производства машины, обрабатывающей все виды тканей, не может быть 125 долл. или меньше. Одно или оба эти ограничения должны быть облегчены, иначе решение найти будет невозможно.
Таким образом, некоторые налагаемые ограничения не могут быть приняты во внимание. Наивно полагать, что все налагаемые ограничения, приводящие якобы к оптимальному решению, должны быть приняты беспрекословно. Большинство решений, принятых администрацией, инженерами и другими специалистами, только приближается к оптимальным. Невозможность прийти к оптимальному решению объясняется такими факторами, как элемент случайности в нахождении решения, сравнительно короткие сроки, отводимые на принятие решения, влияние.готовых решений, сложности и последствия, которые невозможно предвидеть, выделена ли задача в самостоятельную проблему и тот факт, что многие решения являются совсем не объективными, нерациональными, небеспристрастными. В результате инженер часто
\103\
выясняет, что некоторые ограничения нельзя принять, а другие принять можно, но лишь при значительном повышении цены изделия. Таким образом очень часто ограничения не принимают во внимание, конечно после договоренности с теми, кто эти ограничения выдвинул.
Недопустимо также, чтобы инженер считал все решения, принятые до него, ограничениями. Многие новшества обязаны своим существованием инженеру, который не принял автоматически все ограничения как установленные однажды,и навеки.
Ложные ограничения. Рассмотрим простую задачу, в которой требуется соединить эти девять точек четырьмя

прямыми линиями, не отрывая карандаша от бумаги. Некоторые вообще не могут решить эту задачу, а другим требуется довольно много времени на ее решение. А все потому, что они неоправданно и, вероятно, не подозревая об этом, исключают возможность существования линий вне квадрата, образованного точками. Они считают, что проводить линии вне квадрата запрещено, хотя о таком ограничении не упоминалось в условии. Это неоправданное и нежелательное исключение равноправных решений является ложным ограничением. В большинстве случаев ложное ограничение выражено неявно. Оно возникает автоматически.
В задаче с кормами, описанной в гл. 6, многие считали, что корма должны храниться обязательно в мешках, хотя никто не оказал, что именно так и должно быть. Тот факт, что при сознательном рассмотрении ложные ограничения улетучиваются, является лучшим доказательством их иллюзорности. Если их выяснить подробно, то станет очевидной их абсурдность. Для примера обратимся опять к задаче с кормами и предположим, что мы приняли некоторые из характеристик имеющегося решения за ограничения. Корма должны быть нагружены в мешки; мешки должны транспортироваться в хранилище на тележке и нужно укладывать каждый мешок. Все это не более чем характеристики существующей системы, в которых слово «есть» заменено «должно быть».
Большинство людей поразительно легко поддаются ложным ограничениям. Из-за этой склонности и потому,
\104\
что ложные ограничения влекут за собой и недостойные внимания решения, вполне оправданы особые усилия для устранения таких «ограничений». Наиболее эффективный способ избежать их—это, по-видимому, тщательные формулировка и анализ задачи.
Определение критериев
Критерий или критерии, которыми будут пользоваться при нахождении наилучшего решения, должны быть определены в процессе анализа задачи. Проиллюстрируем это положение примером. Предположим, что отличительной чертой нового ружья должно быть его высокое качество. Так как качеству ружья уделяется особое внимание, разработчик подбирает другие материалы, механизмы, и пр., чем при разработке обычного ружья. Главный критерий оказывает воздействие на разработчика при выборе решения, поэтому он (критерий) должен быть известен прежде, чем начались поиски решения.
Определение применения
Если реку нужно пересекать только изредка в данном месте, то решение задачи — мост, по-видимому, не обеспечивает минимальную стоимость (проект плюс строительство плюс стоимость переправы). С другой стороны, если миллионам людей необходимо в данном месте пересекать реку в течение определенного времени, лодка также не окажется предпочтительным решением, хотя она и удовлетворяет критерию минимальной стоимости. Количество переходов из состояния А в состояние В здесь становится главным независимо от общей стоимости. Вспомним разработку метода производства телефонных реле. Если бы их требовалось только несколько тысяч, то разработчик выбрал бы наверняка другое решение. А поскольку переключателей нужно было много миллионов, инженер, естественно, рассмотрел различные виды автоматов для выполнения этой работы. Разработка и строительство такой машины сравнительно дороги, но окупаются ее высокой производительностью. Если в случае задачи со стиральной машиной стирать нужно будет только несколько раз, то такое редкое употребление должно быть учтено при.конструировании. Если же машину нужно применять тысячи раз, то ее материалы,
\105\
механизмы и пр. будут совсем другими. Разработчик стиральной машины, или любого другого прибора, конструкции или технологического процесса должен определить ожидаемое применение (т.е. как интенсивно будет.использовано решение), так как это сильно влияет на то, какое решение будет в этих условиях оптимальным. Таким образом, очень важно как можно точнее определить применение решения еще в процессе анализа задачи, так как знание этого помогает инженеру направить поиски решения в наиболее выгодную область. Эта информация также необходима инженеру для принятая разумного решения о времени, требуемом ему для проектирования.
Определение объема производства
Предположим, что нужно изготовить только десять стиральных машин. Решая эту задачу, разработчик будет мало обращать внимания на технологичность изготовления машины. Нестандартные дорогие детали, ручная работа и сборка—,все это может быть применено, поскольку машин выпускается только десять. Совсем иное дело, если (нужно изготовить 300000 машин. В этом случае инженер -глубоко заинтересован в том, как влияют на общую стоимость машины стоимость различных деталей, применяемых в. ней. Существует разница между тем, как часто применяют машину, и количеством машин, которое нужно изготовить. Последнее называется объемом производства и оно определяет, какое решение задачи окажется оптимальным.
Стараясь определить применение и объем производства, инженер должен попытаться точно предсказать общую тенденцию, а также циклические и случайные отклонения. Ошибка в определении может привести к конфузу. Представьте себе, как будет реагировать публика на создание инженерами сверхскоростного шоссе, которое, судя по объявлениям, должно удовлетворять нужды транспорта в течение 10 лет и которое на самом деле станет непригодным через полгода после пуска.
Выводы
На рис. 7-3 отмечены виды информации, которые ип-женер должен получить при анализе задачи. Применяя эти терминологию и систему обозначений, задачу мож-
| Вход (состояние Л) | Состояние дел, существующее Перец выполнением необходимого преобразования, например загрязненные ТК2 НЧ |
| Входные переменные | Характеристики входа, которые могут изменяться во времени, например могут быть различные типы тканей, их вес, объем и количество грязи на них. |
| Входные постоянные входные ограничения) | Ограничение свойств в выходной переменной (например, содержание влаги не должно превышать 30%). |
| Переменные решения переменные проекта, па->аметры проекта) | Изменяемые характеристики решения, например размеры прибора, его вес и материалы, применяемые при его создании |
| Ограничение | Ограничение свойства, которое может принять переменная решения, например прибор не должен быть больше чем 75 см в ширину, 95 см в высоту и 75 см R лтт ину |
| Критерий (мера эффективности) | Основа, на которой производят сравнительную оценку возможных решений, например стоимость производства. |
| Объем | Сколько раз будет воспроизведено решение (например, будет построено 300000 стиральных машин). |
| Применение | Как долго можно пользоваться данным решением для выполнения нужного преобразования, например владелец стиральной маглины может воспользоваться ею приблизительно 1 500 раз. |
Рис. 7-3. Терминология, используемая при инженерном проектировании.