Таблица 2
Отклонения прибытия поездов от расписания
| +2 мин* | + 13 | +2 | +6 | +9 | —I | +4 | +5 | +11 | +8 |
| +8 | + 11 | +4 | +5 | + 13 | +2 | —2 | + 11 | +5 | +2 |
| + 12 | +8 | +6 | +2 | +21 | +5 | +3 | +20 | +8 | +5 |
| —6 | +5 | +9 | + 15 | + 17 | +9 | +7 | + 1 | +20 | |
| + 1 | +5 | +7 | +9 | +3 | +8 | +4 | —1 | + 11 | |
| +4 | + 14 | + 10 | + 10 | +3 | —3 | +5 | + 1 | +7 | +7 |
| +6 | _ з | + 12 | +8 | +5 | + 3 | +7 | +6 | +9 | + 3 |
| +6 | + 17 | + 12 | —4 | +4 | — 12 | + 16 | +6 | ||
| + 1 | +2 | +6 | +5 | +8 | + 10 | —1 | +4 | +2 | + 16 |
| + 3 | + 11 | +3 | +2 | +6 | +7 | —10 | +9 | +7 | +4 |
| + 10 | +5 | — 1 | —7 | + 19 | +4 | +9 | +8 | +4 | +13 |
| +22 | + 1 | —8 | +6 | + 10 | —4 | + 15 | + 13 | —6 | + 2 |
| +4 | + 16 | +3 | +7 | —2 | + 1 | +25 | +29 | + 17 |
* Знак плюс означает, что поезд опоздал на 2 мин.
\075\
Время, необходимое для расформирования прибывшего состава, зависит от числа вагонов в нем. Конечно, это время зависит также от различных случайных величин. Поэтому два состава, имеющие одинаковое число вагонов, будут, вероятно, расформированы за различное время. Данные о формировании составов с различным числам вагонов приведены в табл. 3. Средние размеры составов, видимо, не изменятся в будущем, поэтому при проектировании новой распределительной горки можно учесть данные прошлых лет
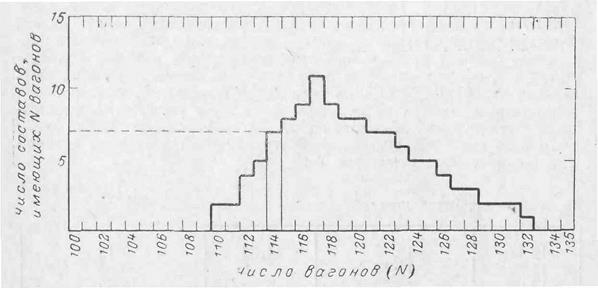
Рис. 4-25. Данные о размерах 120 поездов, представленные в виде частотной гистограммы-. Этот график показывает, что 7 из 120 поездов (17%) состоят из 114 вагонов.
о количестве вагонов в составах. Эти же данные могут быть учтены при определении производительности новой горки. Данные о размерах составов приведены на рис. 4-25 в виде графика. (Эти данные, представленные в виде графической модели, называют частотной гистограммой; она является удобным и эффективным способом представления большого числа наблюдений.)
Вас попросили осуществить цифровое моделирование процесса формирования составов. Для этого составьте таблицу по примеру той, которая приведена на стр. 57.
Таблица 3
|
|
Данные о формировании составов
| Число вагонов в составе | Время формирования, мин | Число вагонов в составе | Время формирования, мин |
| 36,8 | ПО | 32,8 | |
| 34,2 | 37,9 | ||
| 37,7 | 35,4 | ||
| 36,0 | 38,6 | ||
| 41,0 | 34,4 | ||
| 35,8 | НО | 29,7 | |
| 39,8 | 39,1 | ||
| 33,5 | 33,8 |
\076\
Сеё помощью вы сможете отмечать время прибытия составов, время начала и конца формирования состава, время ожидания и пр. Для моделирования необходимо принять некоторые предположения. Первое — отсутствие связи между временем прибытия составов по расписанию и числом вагонов в них. Другое — составы будут формироваться в порядке их прибывания.
Отклонения от расписания можно моделировать с помощью метода Монте-Карло. Простейший способ воспользоваться этим методом — написать на листках бумаги числа, приведенные в табл. 2, и
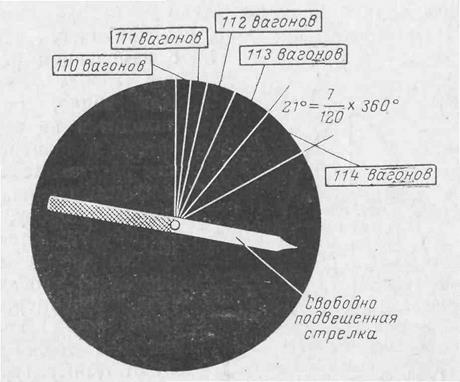
Рис. 4-26. Круговая частотная гистограмма, объединенная со свободно подвешенной стрелкой, может быть использована для определения числа вагонов в данном поезде. Для иллюстрации того, как составлена гистограмма, показано построение сегмента, соответствующего количеству поездов, состоящих из 114 вагонов. Генератор случайных величин, построенный по такому принципу, показан на стр. 56.
перемешать их. Затем, чтобы определить отклонение от расписания, нужно взять любой из листков. Время, указанное па листке, покажет отклонение времени прибытия состава от указанного в расписания.
Для определения числа вагонов в составе можно воспользоваться тем же способом вытягивания бумажек из шапки, что и в предыдущем случае. Иначе число вагонов можно определить с помощью рулетки, показанной на рис. 4-26. Чтобы приготовить такой прибор, нужно нанести данные рис. 4-25 по окружности.
|
|
Смоделируйте по крайней мере десяток прибытий поездов. Включите в Ваш отчет объяснение процесса моделирования и краткое изложение предположений, которые Вы приняли ib добавление к тем двум, которые были описаны выше.
\077\
Глава пятая. ОПТИМИЗАЦИЯ
Термин оптимальный означает лучший с точки зрения данных критериев. Как Вы знаете, существует определенное положение фокусирующей линзы, при котором рассматриваемое изображение самое четкое. Критерием в данном случае является четкость изображения. На рис. 6-1 графически показано, как изменяется четкость с изменением расстояния между линзами. Как видно, оптимум находится на вершине кривой и по мере того, как расстояние между линзами изменяется в любую сторону, четкость ухудшается. Подобные кривые встречаются во многих случаях, например, скорость роста колонии бактерий также зависит от температуры организма.
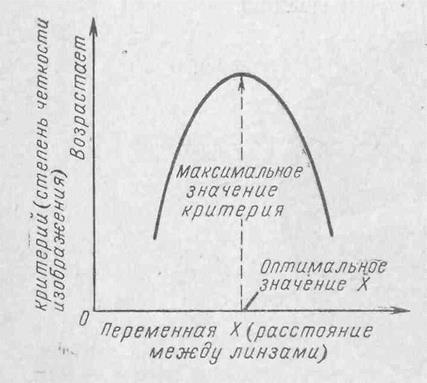
Рис. 5-1. Графическое представление понятия оптимума.
В этом случае переменная X на рис. 5-1—температура, а критерий — скорость роста. Как показывает эта кривая, существует определенная температура, при которой скорость роста максимальна. Это и есть оптимальная температура с точки зрения скорости роста, являющейся критерием. Такая же зависимость наблюдается между скоростью выполнения работы и общим ее количеством, совершенным за определенное время, между стоимостью товара и доходом от его продажи, между температурой в помещении и комфортом и пр. В каждом случае имеется оптимальное значение независимой переменной, например скорости выполнения работы, цены, температуры.
|
|
Понятие оптимума чрезвычайно важно в инженерном деле, так как почти каждая инженерная задача имеет оптимальное решение. Более того, из многих характеристик оптимального решения только несколько не имеют
\078\
оптимального значения. Например, есть оптимальная скорость подачи топлива с точки зрения эффективности работы двигателя, оптимальная жесткость щетины с точки зрения очищающей способности механической зубной щетки, оптимальные размеры и форма кофейника, позволяющие максимально легко им пользоваться, и оптимальная мощность гидростанции.
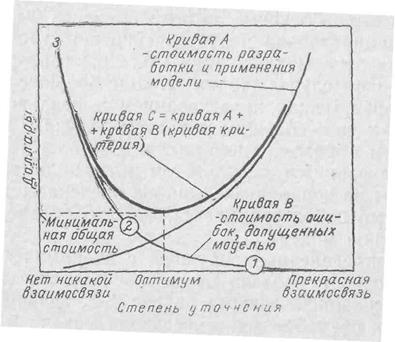
Рис. 5-2. При разработке предсказывающих моделей должен быть достигнут компромисс между двумя противоречивыми критериями—стоимостью разработки и применения предполагаемой модели и затратами, связанными с ошибками, допущенными моделью.
Понятие оптимума применимо к работе инженера, так же как и к его решениям. Так, например, существуют оптимальное количество времени, которое следует уделить той или иной задаче, и оптимальная степень точности, с которой нужно изготовить модель. В последнем случае, поскольку дополнительные усилия направлены на улучшение связи между результатом, предсказанным моделью, и действительным результатом, становится значительно труднее применять улучшенную модель. Общую связь между тем, как близко модель соответствует реальной жизни, и затратами на Осуществление такой связи показывает кривая А на рис. 5-2.
По мере того как стоимость разработки модели возрастает из-за дополнительных затрат на повышение точности, другие важные затраты уменьшаются (кривая В). Эта кривая показывает, как дорого стоят ошибку при использовании моделей.
\079\
Пусть, к примеру, проектировщики химического завода полагаются в своей работе «а некоторую модель. Если после того, как завод будет построен, обнаружится небольшое несоответствие между тем, что предсказала модель, и что получилось в действительности, его сочтут неизбежным. В этом случае стоимость этого несоответствия незначительна, как показано на рис. 5-2 (криваяS, точка 1). Бели бы несоответствие было большим, то потребовалась бы некоторая модификация завода после завершения строительства и стоимость этой модификации была бы гораздо больше, чем в первом случае (точка 2). Еще большее отсутствие взаимосвязи между предсказанием и реальностью привело бы к еще большим затратам (точка 3 на кривой В). Таким образом, с повышением несоответствия между предсказанным результатом и реальностью растут и затраты на исправление ошибок предсказывающей модели. Само собой разумеется, что это справедливо для любого типа модели.
Для определения наилучшей с экономической точки зрения точности модели нужно воспользоваться обоими графиками, приведенными на рис. 5-2: графиком общей стоимости разработки и применения модели и графиком стоимости ошибок, допущенных в результате неточного предсказания. Оптимальной при этом является точка С на рис. 5-2. Такое же положение существует и при разработке измерительных систем. Если при все возрастающих усилиях инженеров результаты начинают ухудшаться, то это говорит о том, что здесь имеется оптимум с точки зрения точности прибора и усилий инженеров. Таким образом, понятие оптимума касается многих аспектов инженерной работы. Оно руководит многими действиями инженера, диктует решения и является доминирующим как в самом решении, так и в способе его достижения.
Оптимизация
Оптимизация — процесс поисков оптимального решения или оптимальных условий. Фокусировка бинокля — вот простейший пример оптимизации. В большинстве инженерных задач этот процесс гораздо сложнее, главным образом потому, что при этом существуют не два, как в предыдущем случае, а много противоречивых критериев.
Противоречивые критерии. Телезритель, настраивая свой приемник, стремится получить четкое изображение при хорошем звуке. Если наиболее четкое изображение и высокое качество звучания достигаются при одном и том же положении рукоятки настройки, то задача тривиально проста, как и при фокусировке бинокля. Предположим, однако, что оптимум звука и изображения не совпадают: при достижении максимальной четкости звук
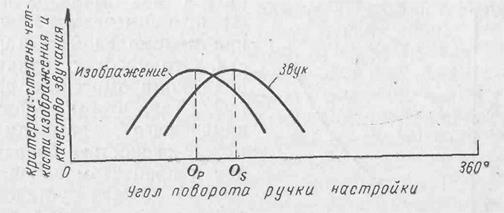
Рис. 5-3. Графическая модель зависимости между четкостью изображения и качеством звучания. Ор предполагает оптимальную четкость изображения; Os — оптимальное качество звукового сопровождения.
становится плохим и наоборот. Такое положение графически представлено на рис. 5-3. Тогда зритель должен найти компромисс между двумя противоречивыми критериями— четкостью изображения и качеством звучания, противоречивыми в том смысле, что при улучшении одного показателя ухудшается другой. Прежде чем искать компромисс, телезритель должен решить, что ему важнее — четкость изображения или качество звука. Хотя каждый телезритель имеет на этот счет особое мнение, все же для большинства компромиссом будет точка в середине между оптимумами Ор и Os на рис. 5-3.
Инженерная практика изобилует такими положениями, когда нужно найти компромисс между противоречивыми критериями. Однако обычно в противоречие вступают не два, а много критериев. Рассмотрим, к примеру, задачу разработки машины для сбора цитрусовых плодов. Инженер должен принять во внимание следующие специфические критерии: скорость сбора плодов, безопасность сборщика, процент порчи плодов при сборе машиной (битые плоды), стоимость работы, стоимость создания машины и ее ремонта. Положение нашего инженера подобно тому, в котором находится упомянутый
\081\
нами телезритель. Если, например, инженер повысит безопасность машины, то скорость сбора неизбежно уменьшится и возрастет стоимость конструкции. Если же уменьшить процент порчи плодов, то автоматически уменьшится скорость сборки и увеличится стоимость конструкции.
Инженер должен принять во внимание все эти несовместимые критерии и в окончательном решении добиться максимальной поль-
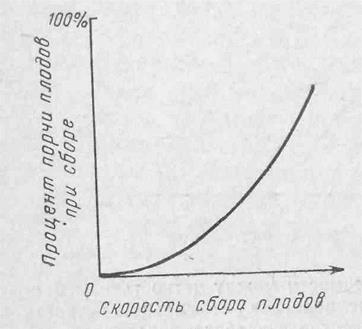
Рис. 5-4. Графическая модель зависимости между двумя из нескольких критериев, используемых инженером при разработке машины для сбора цитрусовых плодов. Он разработал эту модель в помощь себе для нахождения оптимального компромисса между этими двумя критериями.
зы от применения машины при минимальной ее стоимости. Это требует принятия ряда компромиссных решений. Так, чтобы добиться наилучшего компромисса между скоростью сбора плодов и процентом порчи, инженер должен установить зависимость между этими двумя критериями. На основе предыдущего опыта и собственных экспериментов инженер установил, что процент повреждения плодов зависит от скорости сбора приблизительно так, как показано на рис. 5-4. С помощью этой модели инженер может уже предсказать, насколько уменьшится брак, если он пожертвует определенной скоростью, или что даст некоторое превышение скорости с точки зрения повреждения плодов. Так размышляя, инженер выясняет, какой же должна быть скорость, чтобы было оптимальным соотношение между двумя этими критериями.
Сравнительная оценка. Инженер не сумеет достичь компромисса между несколькими критериями, не оценив сравнительной важности каждого из них, что, к сожалению, сделать не так легко. Знание зависимости, показанной на рис. 5-4, мало поможет инженеру, если он не изучил важность различных скоростей и процента повреждения плодов для тех людей, кто в дальнейшем будет эксплуатировать машину. Возможно, что большинство людей, работающих на машине, предпочтут рабо-
\082\
тать на высоких скоростях и в жертву скорости принесут довольно высокий процент повреждения плодов. А раз так, то инженер должен разумно оценить необходимость такой жертвы на фоне остальных критериев, с тем чтобы весь проект был оптимальным.
Определение сравнительной ценности (сравнительных весов) противоречивых критериев часто называют сравнительной оценкой. Когда телезритель решает, что ему важнее — четкость изображения или качество звучания, он совершает сравнительную оценку. В инженерной работе бывает трудно совершить эту оценку еще и потому, что инженер должен также предвидеть то, как оценят тот или иной критерий потребители. Так, например, разработчик механической зубной щетки должен определить, пожелает ли значительная часть потребителей заплатить на X долл. больше, чтобы избежать неудобств и опасности, связанных с применением соединительного шнура с вилкой, включающейся в электросеть.
Сравнительная оценка наиболее сложна при разработке систем, связанных с риском для человека. Так, проектировщики скоростной автострады должны рассмотреть такие критерии, как стоимость строительства, пропускная способность, безопасность, долговечность и стоимость ремонта. Стоимость строительства и безопасность— противоречивые критерии. Стенка, разделяющая автостраду на два проезда на две трети сокращает число несчастных случаев, но удорожает строительство на 750000 долл. Стоит ли дополнительная безопасность таких затрат? Некоторые проектировщики считают, что дополнительные расходы «а безопасность оправдываются, если благодаря им будет спасена хотя бы одна жизнь. Другие, зная, что на многих автострадах таких стенок нет, будут против дополнительных расходов при строительстве новой автострады.
Нахождение оптимума. К сожалению, не существует прямого пути нахождения оптимального решения задачи. В большинстве случаев инженер должен полагаться на несколько методов нахождения оптимума, сочетание которых позволяет ему переходить от одной ситуации к другой. Эти методы формальны и строги. Одним из таких формальных методов является метод, описанный ниже.
Модели всегда основаны на возможности оптимизации. Приведенный ниже пример показывает наиболее
\083\
общий способ применения математики для оптимизации. Инженеры-автодорожники решили определить оптимальную скорость потока транспорта через один из оживленных туннелей Нью-Йорка. Они наблюдали потоки транспорта, проходящие через туннель, чтобы определить зависимость между интервалом между машинами и их средней скоростью. Результаты их исследований приведены на рис. 5-5 в виде точек, соединенных кривой.
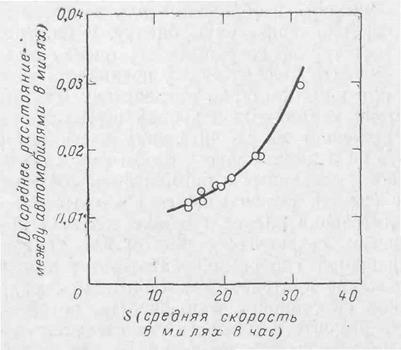
Рис. 5-5. Результаты измерения скорости и расстояния между машинами, движущимися в туннеле. Кривая, проведенная через полученные при измерении точки, показывает зависимость между скоростью и расстоянием между машинами,
Уравнение этой кривой, а следовательно, математическая модель зависимости интервала между машинами от скорости их имеет вид:
где D — среднее расстояние между машинами, миль/маш; S — средняя скорость этих машин, миль/ч.
Число машин, проходящих через туннель за определенный интервал времени, прямо пропорционально их средней скорости и обратно пропорционально среднему расстоянию между ними, т. е.
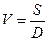маш/ч.
\084\
Преобразовав это выражение в
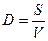
и объединив его с выражением (1), получим:
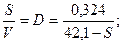
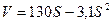
График этой математической модели показан н рис. 5-6. Форма его уже знакома нам. Оптимальную скорость теперь можно
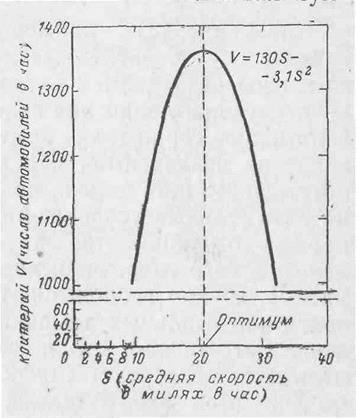
Рис. 5-6. Графическое представление зависимости между средней скоростью автомобиля и числом автомобилей, проходящих через туннель за час (V). График показывает, что с точки зрения этого критерия существует оптимальная скорость 21 миль/ч.
визуально определить; максимуму соответствует скорость 21 миль/ч (около 34 км/ч). Другими словами, оптимальная скорость 21 миль/ч удовлетворяет критерию наибольшей пропускной способности туннеля. Тот же результат можно получить, совершив элементарные вычисления. Продифференцировав выражение (3) по S, получим:
где dV/dS —наклон кривой, показанной на рис. 5-6.
Из уравнения (4) и рис. 5-6 очевидно, что этот наклон различен при различных значениях 5. Мы знаем, что на вершине кривой, где Vмаксимально, этот наклон равен нулю. Таким образом, остается определить значение S, при котором
то есть 
Решив это уравнение, найдем, что оптимальным значением является 21 миль/ч. Это простой пример, но он
\085\
показывает, как полезны математические модели при оптимизации.
Уравнение (3) —пример выражения, которого стремится достичь инженер при нахождении оптимума. Оно математически описывает связь между критерием и зависимыми переменными (в нашем примере единственной зависимой переменной была скорость). Знание математической зависимости критерия от независимых переменных— мощное оружие инженера при нахождении оптималшого решения задачи.
Оптимизирующие модели типа вход—выход
Уравнение (3) — пример модели типа вход — выход. В этом случае численные значения (вход) могут быть заменены независимой переменной для определения результирующего значения зависимой переменной (выход). С помощью серии таких замен можно найти оптимальное значение независимой переменной. В отличие от этого оптимизирующая модель позволяет найти непосредственно оптимальные условия. Модель управления процессом производства цемента, описанная в гл. 4, является моделью такого типа. Зная характеристики исходных материалов,- можно воспользоваться уравнением для определения оптимальных, температуры и скорости вращения •печи. Естественно, что поскольку оптимизирующая, модель дает непосредственный результат, ее предпочитают модели типа вход — выход, но создать такую модель гораздо труднее, чем модель типа вход—выход.
Все моделирование основано на создании моделей типа вход — выход. Принимаются определенные условия (вход), ставится эксперимент -и наблюдается результат (выход). Этот процесс может быть повторен несколько раз для исследования оптимальных условий.
Оптимум как цель работы
Оптимум—основная и чрезвычайно важная цель, к которой стремится инженер в своей работе. Он ищет оптимальное решение и старается применить его. (Заметьте, что мы сказали не добиться, а стараться достичь оптимума.) Хотя оптимальное решение почти всегда — цель инженера, она, однако, не всегда достижима. Существует много задач, настолько сложных, что найти
\086\
их оптимальные решения за период времени, отведенный на разработку, не представляется возможным. Во многих случаях время, необходимое для нахождения оптимального решения, больше, чем время жизни самой задачи. Существует много других задач, ждущих, когда инженеры обратят на них внимание, и часто инженер принесет больше пользы, переключившись на решение •новой задачи, чем продолжая поиски оптимального решения старой.
Упражнения
1. Для любых двух из перечисленных ниже приборов, устройств или технологических процессов назовите критерии, которые должен учесть разработчик. Определите противоречивые критерии:
а) перекресток двух автострад;
б) гигантский океанский лайнер;
в) искусственная рука;
г) автомобиль;
д) автомат, производящий колбы для электроламп;
е) фабрика бытовых холодильников;
ж) любой из примеров, описанных в гл. 1.
2. Придумайте десять ситуаций, в которых, по Вашему мнению, существует оптимальное значение некоторой переменной по отношению к установленному критерию. (Например, существует оптимальная скорость чтения по отношению к объему приобретаемых знаний.)
Глава шестая. ПРОЦЕСС ПРОЕКТИРОВАНИЯ. ФОРМУЛИРОВКА ЗАДАЧИ
Процесс решения инженерной задачи в основном состоит из поисков оптимального решения среди тех, которые удовлетворяют условиям. Ниже описывается общая методика нахождения этого решения. Эта общая методика с небольшими изменениями называется процессом проектирования. Описанию этого процесса посвящены следующие пять глав.
Общая методика решения задачи
Первый логический шаг при решении любой задачи — определение этой задачи. О том, что такое инженерная задача и как она определяется, мы говорили в начале этой книги. Вот пример определения знакомой нам задачи,
\087\
Состояние А. Молодой человек, только что закончивший среднюю школу.
Состояние В. Тот же человек, преуспевающий в жизни, имеющий семью, пользующийся авторитетом у сослуживцев-
Ограничения. Переход из состояния А в состояние В должен произойти законными путями.
Критерий. Трудности в достижении цели, время, долг перед обществом.
Говорят, что правильно определить задачу — это значит почти решить ее. Сказано, конечно, слишком сильно, но большая доля правды здесь есть. Инженер, решающий задачу, должен вникнуть в суть существующих решений, для того чтобы понять истинную природу задачи. Это требует знания основных характеристик задачи, настойчивости и, вероятно, большего времени, чем мы склонны уделять этой важной фазе решения.
За определением задачи следуют поиски возможных решений. Эта фаза решения задачи требует наведения справок, поисков, исследований и другой деятельности, чтобы сформулировать решения имеющейся задачи, достойные внимания.
Третий этап в методике решения инженерных задач— процесс принятия решения. Большинство найденных решений, несомненно, неодинаково, и их нужно оценить для определения предпочтительного решения. Это процесс отбора, основанный на известных критериях, в результате которого находят предпочтительное решение.
Процесс проектирования
Предпочтительна следующая последовательность в решении типовой инженерной задачи.
Формулирование задачи. При этом задачу определяют в общем, не вникая в детали; выделяются состояния А и В.
Анализ задачи. Определяются все детали задачи, производятся необходимые исследования для получения информации о специфических особенностях задачи.
Поиски возможных решений. Некоторые решения инженер изобретает сам, другие познает, знакомясь с литературой.
Принятие решения. Оценка возможных решений, их сравнение и нахождение наилучшего.
\088\
Уточнение решения, в результате чего дается полное описание решения со всеми его характеристиками.
Описанный процесс, называемый процессом проектирования, почти полностью совпадает с методикой нахождения решения и отличается от нее только двумя моментами. Во-первых, тем, как определяется задача.
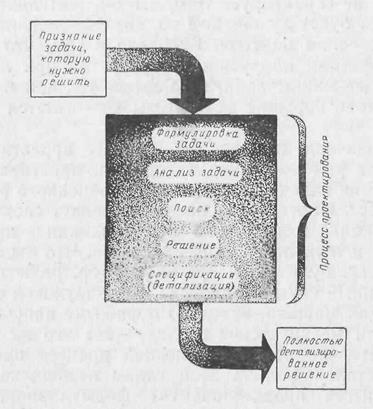
Рис. 6-1. Процесс проектирования начинается с выявления потребности (нужды) и завершается спецификацией средств удовлетворения этой потребности.
Процесс проектирования начинается с определения задачи в общих чертах, а уже затем.следует уточнение деталей. Это делается для того, чтобы предостеречь инженеров от внимания к деталям до ознакомления со всей задачей в целом. Во-вторых, добавляется процесс уточнения решения (спецификация), который необходим, так как при реализации решения инженеру придется работать совместно с людьми, которые утверждают решение, строят прибор, налаживают его и работают с ним.
Опрос инженеров и преподавателей показывает, что применение такого процесса проектирования в течении
\089\
долгого времени приносит наилучшие результаты как с точки зрения качества принимаемого решения, так и цены, которой оно достигнуто. Бывает и так, что самый легковесный подход к решению задачи приносит хороший результат, так как при поисках решения не исключен элемент случайности. Более того, даже нахождение оптимума не гарантирует того, что окончательное решение задачи будет лучше, чем то, которое получено было при легковесном подходе. Все дело в том, что вероятность получения наилучших результатов три легковесном подходе минимальна, в то время как при методическом подходе хорошие результаты достигаются гораздо чаще.
Как показано на рис. 6-1, процесс проектирования охватывает ряд поступков и событий, простирающихся от признания задачи до получения уточненного решения. Это процесс, в котором инженер (Применяет свои знания, квалификацию и интуицию при создании приборов, устройств и технологических процессов. Что бы инженер ни создавал, будь это ядерный реактор, радиотелескоп, искусственный спутник, плотина, сверхзвуковой самолет, печатающая машина, завод по обработке пищевых продуктов или механическое сердце, — всё это он создает, последовательно проходя основной процесс проектирования. Остальная часть этой главы посвящена первой фазе процесса проектирования—формулированию задачи.
Формулирование задачи
Одобряете ли (Вы тех, кто пытается решить задачу, толком не зная, что она собой представляет? Конечно, нет! Однако такой подход к решению задачи все еще нередко практикуется и, естественно; приносит только вред. Имеет смысл ознакомиться с задачей в целом, прежде чем углубляться в детали. Первое, что нужно сделать при формулировании задачи, — это определить ее ib_общих чертах и решить, стоит ли ею вообще заниматься. Этот период [критического осмысливания задачи обычно отнимает небольшую часть времени, отведенного на решение задачи. То обстоятельство, что иногда на это может потребоваться всего несколько минут, не умаляет важности формулирования задачи в процессе проектирования.
\090\
Формулирование задачи производства и хранения кормов
Дирекция крупной организации, производящей и распределяющей животноводческие корма, обеспокоена сравнительно высокой стоимостью их.производства и хранения. Перед инженером поставлена задача отыскать возможность сократить эти расходы. В настоящее время корма производятся и хранятся по схеме, показанной на рис. 6-2.