Все эти варианты инженер должен анализировать с помощью модели. Упрощенный вариант такой модели показан на рис. 4-10. На этом рисунке случайные элементы и времена событий представлены генераторами случайных величин, показанными в виде окружностей. Главной частью такого генератора, представляющего собой рулетку, является свободно подвешенная
\055\

Рис. 4-10. Схематическое изображение одной из фаз цифрового моделирования. Анализируются операции взлета и посадки на двух взлетно-посадочных полосах аэропорта. Подобная процедура может быть повторена сотни раз для получения окончательных результатов.
\056\
стрелка. Чтобы определить время, необходимое для приземления данного самолета, оператор вручную устанавливает стрелку соответствующего генератора случайных величин, выполняет вычисления и определяет «да» или «нет» в соответствии с действиями, показанными на рис. 4-10.
| Самолет | X | Х+1 | X-f-2 |
| Прибыл в | 7.14* | 7.15 | 7.21 |
| Полоса свободна для посадки в | 7.17* | 7.20 | 7.24 |
| Полоса свободна для следующего самолета в | 7.20* | 7.24 | |
| Подготовка полосы ко взлету в | 7.54* | ||
| Полоса свободна для взлета в | 7.59* | -- | |
| Полоса свободна для приема следующего самолета в | 8.03* | ||
| Время ожидания посадки, мин | -- | ||
| Время ожидания взлета, мин | |||
| Время подготовки полосы, мин | |||
Рис. 4-11. Часть табличной записи, выполняемой при моделировании, показанном на рис. 4-10.
Кроме того, оператор записывает данные в таблицу, показанную на рис. 4-11. Так как в такой системе проектирования основой являются цифры, то она получила название цифрового моделирования.
В основном цифровое моделирование представляет собой серию последовательных цифровых выкладок по определенным правилам, приводящую к тому или иному
* Это время определено с помощью генератора случайных величин, подобного показанному на рис.4-10
\057\
решению. Это позволяет выполнить операции на ЭВМ, так как ручные вычисления очень трудоемки.
Применение ЭВМ для цифрового моделирования становится все более популярным в инженерной практике. В большинстве цифровых моделирующих систем учитывается фактор случайности, подобно тому, как это делалось в рассмотренном выше случае реконструкции аэропорта. Такое моделирование часто называют моделированием по методу Монте-Карло2. Этим методом пользуются в военном деле (теория стратегических игр), на транспорте, в строительстве, на производстве и пр.
Цифровое и аналоговое моделирование дают более точные результаты, чем другие виды моделирования, не говоря уже о том, что они требуют гораздо меньше времени. С помощью цифрового и аналогового моделирования можно экономить годы человеческого труда. Так, например, ЭВМ может решить задачу о реконструкции аэропорта с двумя взлетно-посадочными полосами буквально за несколько минут. Таким образом, аналоговые и цифровые модели в очень короткий промежуток времени могут синтезировать опыт, который мог бы потребовать годы человеческого труда.
Другие виды моделирования
Существуют и другие виды моделирования. Так, например, космонавт на рис. 4-12 хочет осуществить посадку на Луну, сидя в модели космического корабля, установленной в наземной лаборатории. Сигналы о том, как этот «космонавт» осуществляет посадку корабля на Луну, передаются в ЭВМ. Она управляет перемещением телевизионной камеры, направленной на модель Луны. Изображение поверхности ее на телевизионном экране в кабине космонавта создает ему иллюзию полета. На рис. 4-13 показано устройство, с помощью которого моделируются условия работы будущего космонавта.
На рис. 4-14 показано, как с помощью аппаратуры удается моделировать положение многих самолетов в воздухе. Благодаря такому широкомасштабному моделированию удается разрешить все сложные вопросы регулирования движения нескольких реактивных самолетов, приближающихся к аэропорту.
Во всех рассмотренных выше примерах один или несколько человек участвуют непосредственно в моделировании.
\058\
Если два человека или более соревнуются в таком виде моделирования, то его называют «игрой».3 Моделирование с участием человека полезно как для предсказаний, так и для тренировки. Весьма желательно, разумеется, чтобы молодые пилоты учились на своих ошибках,не на самолетах, а на их моделях, создающих

Рис. 4-12. Этот человек тренируется в осуществлении посадки на Луну и стыковки с другим космическим кораблем. В 5 ч пополудни он, однако, пойдет домой, как и большинство других служащих авиафирмы, поскольку полет он совершал о модели космического корабля в лаборатории.
для пилота реальные условия полета, потому что ошибка в реальном полете более печальна, гаем звук сирены, возвещающей об ошибке при тренировке на модели.
Другие устройства, с помощью которых моделируются условия полета, показаны на рис. 4-15 и 4-16. Первое устройство имеет кабину пилота с приборами управления и специальную проекционную камеру, которая проецирует на экран перед пилотом движущийся пейзаж, создавая полную иллюзию полета. Пилот с помощью рычагов управления совершает взлет самолета, его маневры в воздухе и посадку, а аналоговая модель определяет, как ведет себя самолет при тех или иных действиях пилота.
\059\
Снятую картину «полета» затем показывают пилоту на экране, чтобы он мог увидеть, как он управлял самолетом. Такую же процедуру выполняют и во время испытательных полетов. Ощущения пилота при работе на такой модели такие же, как и при работе на реальном самолете. Используемые узлы и системы

Рис. 4-13. Благодаря воздушной подушке (а) опоры конструкции находятся на высоте 2,5 см над полом, устраняя трение между опорами и полом. Воздушные «подшипники» и оси вращения с малым трением (б и в) по существу настолько устраняют действие сил трения, к которым человек привык на Земле, что он может передвигать себя выдыхаемым или вдыхаемым потоком воздуха. Этот прибор применяется для моделирования условий космоса,где нет трения, для оценки способности космонавта выполнять операции, связанные с управлением кораблем, его ремонтом и профилактикой. Когда космонавт пользуется гаечным ключом, он;вращается вместе с ним вокруг гайки.
\060\

Рис. 4-14. На диспетчерском пункте аэропорта проводится широкомасштабное моделирование управления движением самолетов. Каждый из участников осуществляет заранее установленный план полета (выдерживает заданный курс, расписание, скорость, высоту полета и т. д.). По мере того как операторы выполняют план полета, манипулируя рукоятками на пульте, на экране радиолокационной станции, контролирующей движение самолетов, появляются эхо-сигналы от самолетов. Переговоры между пилотом (сидящим в соседней комнате) и диспетчером-руководителем полета ведутся с помощью двусторонней радиосвязи. Так моделируются полеты и управления ими, подобные реальной ситуации в воздухе.
самолета монтируют на раме за пилотской кабиной (см. рис. 4-15). Электрическая аналоговая машина моделирует работу отсутствующих узлов самолета. Подобный метод позволяет оценить работоспособность новых узлов и систем самолета.
Важность пользования методом моделирования
Методы представления, описанные в этой главе, часто называют общим словом «модели». В инженерной терминологии слово «модель» звучит одинаково со словом «представление». Инженер пользуется наглядными" моделями, графическими, математическими и др. Важность и общность этих моделей не всегда становятся сразу же очевидными. В любом случае модель — это подобие реального объекта или процесса, описывающее.структуру и поведение его в реальных условиях.
\061\

Рис. 4-15. Устройство для моделирования полетов, позволяющее инженерам испытать прототип самолета до его постройки. Применение подобных устройств позволяет испытать в полете несуществующий самолет. Устройство позволяет, кроме того, оценить работу некоторых реальных узлов и приборов проектируемого самолета при меньших затратах времени и средств, чем на реальном самолете, и без риска потерь.

Рис. 4-16. Крупный план модели кабины, показанной на рис. 4-15. Кабина с приборами и рычагами управления окружена экраном, на который проецируется движущаяся поверхность Земли. Кабина неподвижна, но изображения на экране движутся в соответствии с действиями пилота, что и создает иллюзию полета. 62
\062\
Рис. 4-17. График изменения скорости воздушных потоков во времени.
Очень большая роль уделяется моделям при обучении инженеров. Курс черчения учит инженера готовить наглядные диаграммы и графические модели и читать их. Курс математики дает возможность научиться обращаться с различными символами и применять на практике такую систему моделирования. При обучении естественным наукам студентов также знакомят с моделями различных структур и их поведением в природе. Обучение во втузе знакомит будущих инженеров с различными моделями и учит их, как и где использовать эти модели при решении инженерных задач.
Модели как помощь в мышлении. Модель облегчает понимание работы системы, устройства и явления, которые с первого взгляда трудно понять. Сложность электронных цепей, производственных систем, химических процессов и механизмов требует графического или какого-либо другого типа моделирования для понимания их действия. Наглядные схематические и графические модели особенно полезны тогда, когда требуется составить себе общее компактное и упрощенное представление о процессе. Размышляя над каким-либо физическим явлением, инженер старается представить его так, чтобы оно было свободно от излишних сложностей, не относящихся к делу. Такая модель позволяет более легко и главное с большей пользой размышлять о природе того или иного явления. Так, например, переменный ток обычно представляют в виде синусоиды на графике, а не в виде потока электронов в проводнике, меняющего направление. Можно судить о порыве ветра по ощущению прохлады на лице. Но инженер, разрабатывающий проект самолета или моста, чаще всего представляет себе такой ветер в графической форме, как показано на рис. 4-17. Таким образом, инженер часто изображает физические явления в виде диаграмм, графиков или математических формул и думает этими категориями, пользуясь ими при анализе того или иного события. Важной целью инженерного образования является
\063\
научить инженеров пользоваться такими абстрактными категориями.
Модели как средство общения. Модели облегчают понимание устройства и работы инженерного сооружения, особенно тем людям, которые должны разрабатывать, строить, использовать и ремонтировать это сооружение. Наглядные (чертежи и графики), словесные и математические модели широко попользуются как средства передачи информации.
Модель как средство предсказания. Решая ту или иную задачу, инженер обычно рассматривает ряд различных вариантов. Для того чтобы установить, какой из них наилучший, он должен определить результат, получаемый от каждого варианта. Модели чрезвычайно полезны для этой цели, так как они позволяют инженеру делать необходимые заключения. Применяя математические или физические модели, можно оценить различные варианты решений за гораздо меньшее время и с гораздо меньшими затратами, чем при экспериментах.
Пусть, к примеру, требуется определить среднее время простоя автомобиля перед разгрузкой -на складе, чтобы оценить, достаточна ли емкость этого склада. Для этого полезна следующая математическая модель:
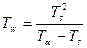
где Tw — среднее время ожидания прибывающего груза; Та — среднее время между прибытием грузовиков для разгрузки; Ts — среднее время, необходимое для разгрузки грузовика*.
Если время прибытия и время разгрузки каждого грузовика известны, то это упрощает решение задачи. К сожалению, как это часто бывает на самом деле, время прибытия грузовиков предсказать нельзя, а время, затрачиваемое на ожидание разгрузки, зависит от случайных величин, размеров и типа груза. Однако в этом случае можно оценить как среднее время между прибытиями автомобилей, так и среднее время разгрузки. Выбирая такую модель как средство
* Такая модель дает удовлетворительные результаты только при определенных условиях, и, конечно, инженер принимает их во внимание. Подобная оговорка может возникнуть и при любой другой модели.
\064\
проектирования, инженер нуждается в некоторой информации. Он должен определить среднее время между прибывающими друг за другом грузовиками и среднее время разгрузки. Необходимо также определить величины Та и Та, чтобы вычислить Тю. Приняв, что Га= 2,3 ч, a Ts=<0,7 ч, среднее время ожидания автомобиля под погрузку получим равным

Процесс предсказания, описанный в этом примере, знаком инженеру. В общем случае он начинается с получения необходимой информации. Источником ее может быть наглядная модель, аналоговая или цифровая ЭВМ, эксперимент в реальной ситуации или опыт инженера. Когда инженер отбирает нужные ему сведения из всей этой информации, он также создает информацию. Очень важной частью работы инженера является определение его требований к содержанию

Рис. 4-18. Роль модели в предсказании результата. Этот процесс начинается с формулировки задачи. Затем, после выбора модели на выходе ее получают информацию.
\065\
информации и способам её получения. Получение необходимый данных часто связано с измерениями, взятием проб, экспериментированием и статистическим анализом (рис. 4-18).
Использование модели для управления. При разработке модели стремятся обеспечить предсказание, возможно более близкое к реальности. Однако в некоторых случаях возможно и обратное: сначала создают модель, а затем пытаются заставить реальный объект вести себя так же, как модель. Так, например, инженерный проект какого-либо сооружения представляет собой модель, и, конечно, это сооружение должно полностью соответствовать модели. Орбита, рассчитанная для космического корабля, — это модель, а весь комплекс аппаратуры, установленной на космическом корабле и в наземном пункте управления, служит для того, чтобы космический корабль летел по орбите, возможно более близкой к расчетной.
На рис. 4-19 приведен другой пример. Для производства высококачественного цемента скорость вращения печи и температура обжига внутри ее должны быть вполне определенными. Их значения должны изменяться по мере того, как меняется химический состав сырья, поступающего в печь. Для того чтобы поддерживать скорость вращения и температуру на необходимом уровне, датчик определяет химические характеристики сырья и передает эту информацию в ЭВМ, в блок памяти которой заложена математическая модель. ЭВМ определяет скорость и температуру при определенном составе сырья, поступившего в печь, и передает эту информацию в приборы управления, регулирующие скорость вращения печи и температуру. Это пример системы управления, некоторые параметры которой контролируются с помощью модели.
Модель — в помощь обучению. Большинство таких моделей, как, например, схемы, чертежи, графики, широко используется для обучения. Более того, моделирование с участием человека очень полезно в тех практических случаях, когда последствия возможной ошибки слишком опасны, как, например, в диспетчерской службе регулирования воздушного движения на аэродроме, в работе пилота и космонавта. Космонавт и весь персонал, участвующий при запуске космического корабля, много раз повторяют программу своих действий на тренировках, до того как космический корабль будет
\066\

Рис. 4-19. Упрощенное представление части цементного завода, иллюстрирующее применение математической модели для управления производством. Для данного производственного процесса существуют наилучшая скорость вращения печи и наилучшая температура внутри нее. ЭВМ вычисляет наилучшие скорость и температуру, получая от датчика информацию о содержании компонентов в сырье. Приборы управления поддерживают наилучшие скорость и температуру, диктуемые им ЭВМ.
запущен на орбиту. Точно так же персонал, обслуживающий ракетные установки, и персонал системы противовоздушной обороны тренируются на моделях без применения своего грозного оружия.
Упрощения, предположения, идеализация
Модель, представленная на стр. 48, предназначена для предсказания объема, занимаемого газом, и называется уравнением состояния идеального газа. При выводе этого уравнения были приняты некоторые предположения о поведении молекул, не соответствующие реальному газу. Однако пользуясь этой моделью» можно предсказать
\067\
поведение почти всех газов, за Исключением газов высокой плотности.
Применяя математическую модель (стр. 64), чтобы определить среднее время простоя автомобиля под погрузкой, необходимо учитывать, что грузовики разгружаются в порядке очереди прибытия на склад я что разгрузка не ускорится, если очередь ждущих разгрузки грузовиков станет длиннее.
В этих примерах и во многих других введение упрощений и предположений позволяет упростить решение задачи. В тех случаях, когда задачи не удается упростить, отбросив некоторые усложняющие факторы, оказывается невозможным применять математику или другие типы моделирования. Более того, во многих практических случаях, если принятые упрощающие предположения не соответствуют реальному положению вещей, они тем не менее не увеличивают ошибки предсказания и не исключают применение модели. Существуют также некоторые упрощения, которые можно принять с небольшим или даже без всякого влияния на применение модели. Так, например, отсутствие сидений в модели самолета, предназначенной для испытания в аэродинамической трубе, никак не влияет на его аэродинамические характеристики. Литая модель также вполне удовлетворит требованиям. Те свойства моделей, от которых мало или вообще не зависят получаемые результаты, вообще не рассматриваются.
Таким образом, для упрощения процесса разработки модели необходимо применять упрощающие предположения. Очень важным свойством квалифицированного инженера является его умение вводить такие упрощающие предположения. Способность упростить задачу без риска значительно увеличить возможность ошибки — большое искусство, которое приходит к инженеру вместе с опытом.
Разработка предсказывающих моделей
При разработке предсказывающих моделей, являющейся основной деятельностью ученого и инженера, обычно придерживаются следующей последовательности:
1. На основании некоторых званий реальной ситуации, которую нужно представить, выбирается модель.
\068\
Например, для определения величины изгиба прямоугольной балки, заделанной в стену (рис. 4-20), можно применить математическую модель вида:

Полный вывод этого уравнения в данном случае не так важен. Важно другое: эта модель позволит вполне удовлетворительно определить степень деформации балки при следующих упрощениях:
груз F действует в одной точке;
материал балки однороден;
груз F воздействует постепенно, а не толчком;
балка жестко заделана в стену.
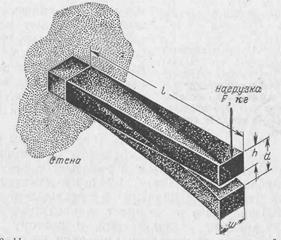
Рис. 4-20. Нагрузка, приложенная на конце прямоугольной заделанной балки, имеющей модуль упругости Е, длину l, ширину w и высоту А, вызывает прогиб балки на величину d.
Насколько возрастет ошибка, если одно из этих упрощений не соответствует реальным условиям? В этом случае способность модели предсказывать неизвестна, и нам понадобится определить и оценить эту способность, прежде чем решиться применить эту модель. Кроме того, нужно установить, даст ли она требуемую точность определения прогиба. В этом частном случае описанную модель применяют на основании некоторых знаний сопротивления материалов под нагрузкой и несложного
\069\
математического аппарата. В других случаях модель создают на основании предварительных экспериментов,, накопленного опыта или на основании дополнительных сведений. Так или иначе, экспериментально выбирают модель, для того чтобы оценить ситуацию *.
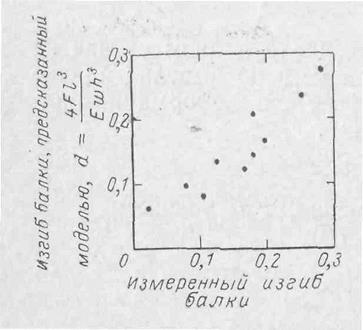
Рис. 4-21. Информационный способ сравнения предсказанного и наблюдаемого результатов. Чем больше рассеяние точек на графике, тем слабее связь между тем, что предсказала модель, и тем, что есть на самом деле,
2. Следующий шаг состоит в сравнении того, что предсказала модель, с тем, что есть в действительности. Для этого проводят серию экспериментов с различными нагрузками консольной балки с различными значениями I, E, w и h и измеряют изгиб балки. Затем, применяя те же значения /, Е, w и h, вычисляют изгиб по нашей математической модели. Для каждого случая мы имеем предсказанный изгиб и полученный на практике. Результаты всей этой работы нанесены на график •на рис. 4-21.
3. Теперь оценим результаты этого сравнения. Оно сделано на рис. 4-22, который показывает результаты двух экспериментов. На рис. 4-22,а предсказанные результаты хорошо совпадают с реальными, а на рис. 4-22,6 предсказание не имеет никакой практической связи с реальными результатами, и поэтому модель в данном случае никакого предсказания не совершает. На основании проведенной оценки должно быть принято решение, может ли применяться наша модель или нет. Соответствует ли разработанная нами модель ре-
* Выбирать модель нужно так, чтобы она была по возможности проклюй и. позволила ввести дополнительные упрощающие предположения. Более того, простая модель необходима по двум причинам: 1) если упрощенная модель достаточно точна, то не потребуется оценивать несуществующие предположения; 2) по опыту известно, что если не удастся разработать модель, свободную от усложнений, то желательный результат получить не удастся. Очень важно сначала разработать сравнительно простую модель, а уж если этот результат достигнут, то можно постепенно исключить нереальные упрощающие предположения.
\070\
реальной ситуации, в которой она будет работать, или нет. Если точность предсказания критическая, если финансовые затраты по отношению к получаемой ошибке высоки, то, видимо, оправданы дальнейшие уточнение и улучшение нашей модели. При этих обстоятельствах мы должны вернуться к п. 1, попытаться уточнить модель и затем повторить весь процесс, как показано на рис. 4-23, до тех пор, пока не придется прекратить эту работу по экономическим соображениям. Если же модель дает точность предсказания, необходимую для применения ее, то мы можем принять модель в представленном виде.
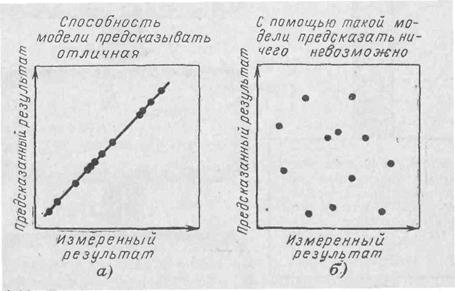
Рис. 4-22. Превосходная связь между предсказанным и реальным результатами (а) и отсутствие такой связи (б), показывающее, что никакой пользы от модели в смысле предсказаний нет.
Результат, подобный показанному на рис. 4-21, вовсе не необычен. Точки не лежат на прямой линии, потому что некоторые предположения, на которых основывается эта модель (см. стр. 69), нарушены. Эта не поддающаяся оценке ситуация, а также ошибки в измерениях d, F и некоторых других величин, неизбежно приводят к тому, что идеальный результат, показанный на рис. 4-22,а, обычно недостижим на практике. Заметьте, что мы сравнивали предсказанный изгиб с измеренным, а не с действительным.
Для того чтобы понять разницу между тем, что предсказывает нам модель, и тем, что мы наблюдаем, необходимо высказать несколько предостережений. Помните, что некоторое различие между предсказываемым и реальным результатами неизбежно.
\071\

Рис. 4-23. Схематическая модель основного процесса, применяемого при разработке предсказывающих моделей.
\072\
Предсказать результат безошибочно невозможно. Собственно говоря, такое предсказание и неэкономично. Оценивая полезность модели, нужно заботиться не о том, отражает или не отражает эта модель реальную ситуацию. На основе такого критерия можно отвергнуть любую модель. Что же является основным при оценке модели? Стоимость. В любом случае существует определенная степень точности, превышение которой экономически невыгодно. Подробнее об этом мы расскажем в следующих главах.
Выводы
Инженер использует наглядные, графические, схематические, словесные, математические и другие модели. Одни из них статически изображают структуру или природу какого-либо предмета, другие — динамически, а некоторые — и то, и другое. Моделирование (приобретение опыта искусственным путем) выполняется с помощью наглядных моделей, аналогов, цифровых вычислений. Все модели несовершенны, и поэтому инженер всегда должен ожидать и принимать во внимание определенную степень несоответствия между моделью и тем, что эта модель представляет. Очень важными понятиями в моделировании являются полезность и унификация модели. Логически эти понятия связаны со многими предметами в инженерном образовании и должны помочь студенту понять важность читаемых ему курсов для его практической деятельности. Способность инженера выгодно использовать технику моделирования для обдумывания решений, передачи информации, предсказаний, тренировок, управления и других целей чрезвычайно важна, так как она дает ему возможность приобрести опыт и мастерство в разработке и оценке моделей.
Упражнения
1. Просмотрите любой учебник и найдите там три примера на каждый из следующих типов моделирования: наглядное, графическое, схематическое и математическое. Снабдите каждый рисунок небольшим словесным комментарием.
2. На каких предположениях основывается уравнение состояния идеального газа, приведенное на стр. 48? Так как реальный газ не удовлетворяет некоторым из этих предположений, не отразится ли это на предсказанном поведении газа? Если Вы не знаете, как бы Вы выловили это?
3. Разработайте модель для предсказания количества времени, необходимого Вам для того, чтобы прочесть различные типы заданий по чтению.
\073\
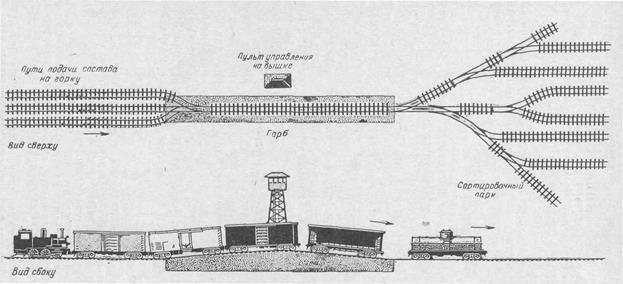
Рис. 4-24. Упрощенное изображение сортировочной системы, показывающей пути подачи состава, где прибывающие поезда дожидаются сортировки, одноколейная горка, через которую должны пройти все вагоны, а также Многоколейный сортировочный парк, на котором формируются новые составы.
\074\
Точность предсказания времени должна быть ±20% Объясните, почему действительное время и предсказанное не совпадают.
4. Крупная железнодорожная станция планирует объединение нескольких сортировочных горок для формирования товарных поездов. Обычно прибывающие товарные поезда формируются с помощью специальных горок, одна из которых показана на рис. 4-24. Расписание прибывающих поездов, подлежащих переформированию, показано в табл. 1. Проектируя новую сортировочную горку и новые пути, инженер, прежде всего, должен определить, может ли эта горка удовлетворительно обслужить поезда при существующем расписании, средний простой прибывающих поездов и число подъездных путей, необходимое для того, чтобы разместить составы, ожидающие переформировки. Для того чтобы определить, какими будут результаты, принимая во внимание имеющееся расписание, инженер должен смоделировать операцию составления поездов. А для этого он должен запастись определенной информацией, на основе которой он и составит модель (см. рис. 4-18).
Таблица 1 Расписание прибытия поездов
| 12.17 | 14.48 | 4.34 | 9.15 |
| 12.49 | 15.19 | 5.00 | 9.55 |
| 13.28 | 15.49 | 5.49 | 10.24 |
| 13.36 | 16.30 | 6.38 | 10.49 |
| 13.51 | 17.57 | 7.10 | 11.03 |
| 14.20 | 21.11 | 7.59 | 11.42 |
| 14.35 | 1.20 | 8.22 | 11.51 |
Инженер знает, что поезда не прибывают точно по расписанию. Результаты исследования опозданий или опережении графика движения поездов сведены в табл. 2.