Дана система двух линейных уравнений: 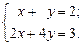
Решением системы является нахождение корней: kx и ky, т.е. таких значений x и y, которые после подстановки в систему обращают уравнения в тождества.
Рассмотрим три варианта решения задачи
Вариант 1
Для решения системы линейных уравнений используем формулы Крамера.
Представим систему в общем виде: 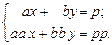
Определители системы вычисляются по формулам:
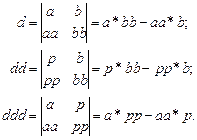
Тогда решением системы по формулам Крамера являются корни: 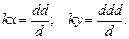
В первом варианте покажем, как можно задавать имена одновременно группе ячеек.
1. В ячейки диапазона A38:A43 введите последовательно наименования коэффициентов системы: a, b, p, aa, bb, pp.
2. В ячейки диапазона B38:B43 введите последовательно соответствующие значения коэффициентов: 1, 1, 2, 2, 4, 3.
3. Выделите диапазон A38:B43 с введенными данными.
4. Выберите команду: Вставка®Имя®Создать…
5. В диалоговом окне в области По тексту установите флажок в столбце слева. Щелкните на кнопке ОК.
6. Щелкая последовательно на ячейках диапазона B38:B43, просмотрите в поле Имя адреса этих ячеек. Теперь ячейки диапазона B38:B43 с числовыми значениями коэффициентов имеют имена, соответствующие именам коэффициентов.
7. В ячейки диапазона C38:C40 введите последовательно наименования определителей: d, dd, ddd.
8. В ячейку D38 введите формулу для вычисления определителя d: =a*bb–aa*b.
9. Выделите ячейку D38 и скопируйте с помощью маркера формулу в ячейки D39 и D40.
10. Выделите ячейку D39 и в строке формул отредактируйте формулу таким образом, чтобы вычислялся определитель dd: =p*bb–pp*b.
11. Выделите ячейку D40 и в строке формул отредактируйте формулу таким образом, чтобы вычислялся определитель ddd: =a*pp–aa*p.
12. Прочтите результат вычисления определителей:
d=2; dd=5; ddd= -1.
Присвоим имена ячейкам диапазона D38:D40 в соответствии с именами определителей.
13. Выделите диапазон C38:D40.
14. Выберите команду: Вставка®Имя®Создать…
15. В диалоговом окне в области По тексту установите флажок в столбце слева. Щелкните на кнопке ОК.
16. Щелкая последовательно на ячейках диапазона D38:D40, просмотрите в поле Имя адреса этих ячеек. Ячейки диапазона D38:D40 с числовыми значениями определителей имеют имена, соответствующие именам этих определителей.
17. В ячейки E38 и E39 введите наименования корней: kx и ky.
18. В ячейку F38 введите формулу для вычисления корня kx: =dd/d.
19. В ячейку F39 введите формулу для вычисления корня ky: =ddd/d.
20. Прочтите результат решения системы уравнений:
kx = 2,5; ky = -0,5
21. Щелкните на кнопке Сохранить на панели инструментов Стандартная.
Вариант 2
Решение системы линейных уравнений по-прежнему проведем по формулам Крамера с той лишь разницей, что определители вычислим, используя функцию матричного исчисления: МОПРЕД. После ввода функции надо нажать не просто клавишу [Enter], а комбинацию клавиш [Shift]+[Ctrl]+[Enter], причем нажимать клавиши надо следующим образом: при нажатых клавишах [Shift]+[Ctrl] нажать клавишу [Enter].
1. Объедините ячейки С45:D45 и поместите в центре заголовок Матрица1.
2. В диапазон ячеек С46:D47 введите коэффициенты системы:
3. Объедините ячейки С49:D49 и поместите в центре заголовок Матрица2.
4. В диапазон ячеек С50:D51 введите коэффициенты:
5. Объедините ячейки С53:D53 и поместите в центре заголовок Матрица3.
6. В диапазон ячеек С54:D55 введите коэффициенты:
7. Выделите ячейку E45 и введите имя d.
8. Выделите ячейку F45 и вызовите мастер функций fx.
9. В диалоговом окне Мастер функций – шаг 1 из 2 из списка Категория: выберите элемент Полный алфавитный перечень, а затем в области Выберите функцию: выберите функцию МОПРЕД.
10. В открывшемся диалоговом окне Аргументы функции щелкните в поле Массив, после чего выделите диапазон ячеек С46:D47 с элементами Матрицы1.
11. Нажмите клавиши [Shift]+[Ctrl]+[Enter]. Прочтите результат (d =2).
12. Выделите ячейку E49 и введите имя dd.
13. Выделите ячейку F49 и вычислите в ней определитель Матрицы2 (dd =5).
14. Выделите ячейку E53 и введите имя ddd.
15. Выделите ячейку F53 и вычислите в ней определитель Матрицы3 (ddd = -1).
16. Выделите ячейку G49 и введите имя kx.
17. Выделите ячейку H49 и введите формулу: = F49/F45.
18. Выделите ячейку G53 и введите имя ky.
19. Выделите ячейку H53 и введите формулу: = F53/F45.
20. Прочтите результат решения системы уравнений:
kx = 2,5; ky = -0,5
21. Щелкните на кнопке Сохранить на панели инструментов Стандартная.
Вариант 3
Решим систему линейных уравнений с использованием обратной матрицы. Решение заключается в умножении обратной матрицы коэффициентов при неизвестных на матрицу (вектор-столбец) свободных членов. Для этого потребуются функции: вычисление обратной матрицы МОБР и умножение матриц МУМНОЖ. Необходимо помнить, что после ввода функций надо нажать клавиши [Shift]+[Ctrl]+[Enter].
1. Выделите ячейку C57 и введите заголовок Матрица свободных членов.
2. В диапазон ячеек C58:C59 введите вектор-столбец свободных членов системы:
3. Выделите ячейку G57 и введите заголовок Решение.
4. В ячейку F58 введите имя kx.
5. В ячейку F59 введите имя ky.
6. Выделите мышью диапазон ячеек G58:G59, в который должен поместиться результат.
7. Вызовите мастер функций fx и выберите функцию МУМНОЖ.
8. В открывшемся диалоговом окне Аргументы функции в поле Массив1 введите название функции для вычисления обратной матрицы: МОБР, а затем в круглых скобках в качестве аргумента укажите диапазон матрицы коэффициентов системы С46:D47 (Матрица1). Для указания диапазона можно просто выделить его мышью.
9. Щелкните в поле Массив2 и выделите диапазон матрицы свободных членов C58:C59.
10. Нажмите клавиши [Shift]+[Ctrl]+[Enter]. Прочтите результат:
kx = 2,5; ky = -0,5
11. Щелкните на кнопке Сохранить на панели инструментов Стандартная.
Контрольные задания
1. Откройте файл Учебный.xls и покажите содержимое Листа2.
2. Щелкая поочередно на ячейках диапазонов J5:J7 и K5:K7, покажите формулы, записанные в этих ячейках.

3. Откройте Лист1 и покажите его содержимое.
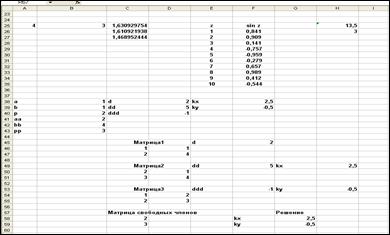
4. Покажите формулы в ячейках H25 и H26 (СУММ и СЧЕТ).
5. Покажите адреса в ячейках A25 и B25 (x и y).
6. Покажите формулы в ячейках C25, C26 и С27.
7. Покажите формулу в ячейке F35 (=SIN(z)).
8. Покажите адреса в ячейках диапазонов B38:B43 и D38:D40.
9. Покажите адреса в ячейках F38 и F39. Адреса не изменились.
10. Покажите формулы в ячейках F45, F49, F53 (вычисление определителей) и H49 и H53 (решение системы).
11. Выделите диапазон G58:G59 и покажите формулу решения системы (функции МУМНОЖ и МОБР).
12. Закройте Excel с сохранением изменений, а затем закройте папку Excel 251.
.
Лабораторная работа № 6
Диаграммы
Понятие диаграммы
Диаграмма – это графическое представление данных. Программа Excel позволяет создавать различные типы диаграмм. Тип диаграммы следует выбирать в зависимости от вида данных. Наиболее распространены следующие типы диаграмм:
· гистограмма и линейчатая диаграмма используются, когда необходимо сравнивать отдельные значения элементов;
· круговая диаграмма используется, когда необходимо показать отношение отдельных элементов к их сумме;
· график используется, когда необходимо отследить изменения отдельных элементов с течением времени.