Первообразная и неопределенный интеграл: основные
Определения и теоремы
В первом семестре мы подробно изучали операцию дифференцирования, которая играет важную роль, как в самом математическом анализе, так и в его приложениях. Не менее значительную роль играет и обратная операция – восстановление функции по ее производной. Эту операцию называют интегрированием.
Определение 1. Функция  называется первообразной для функции
называется первообразной для функции 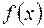 на данном промежутке, если на этом промежутке выполняется равенство:
на данном промежутке, если на этом промежутке выполняется равенство:
 .
.
Например, для  первообразная
первообразная  , ибо
, ибо  .
.
Всякий раз, когда математики вводят в рассмотрение операцию, обратную некоторой известной операции, возникают два вопроса:
1) всегда ли осуществима эта обратная операция?
2) однозначен ли результат этой операции?
Ответ на первый вопрос дает теорема существования первообразной, доказательство которой будет дано в теме «Определенный интеграл».
Теорема 1. Всякая непрерывная функция имеет первообразную.
Что касается второго вопроса, то ответ на него отрицательный: если у функции 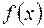 есть первообразная
есть первообразная  , то любая сумма
, то любая сумма  , где
, где  const будет первообразной для
const будет первообразной для 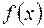 , ибо
, ибо  , а
, а 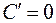 . Интересен и такой пример: для функции
. Интересен и такой пример: для функции  первообразными являются функции
первообразными являются функции 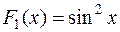 ,
,  и
и  . Но в бесконечном множестве всех первообразных для любой функции существует определенный «порядок», устанавливаемый следующей теоремой.
. Но в бесконечном множестве всех первообразных для любой функции существует определенный «порядок», устанавливаемый следующей теоремой.
Теорема 2. Пусть  – некоторая первообразная для функции
– некоторая первообразная для функции 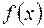 на промежутке
на промежутке  . Тогда любая другая первообразная
. Тогда любая другая первообразная  имеет вид
имеет вид  , где C – некоторая постоянная.
, где C – некоторая постоянная.
Доказательство. Вспомогательную функцию  рассмотрим на промежутке
рассмотрим на промежутке  и применим к ней теорему Лагранжа:
и применим к ней теорему Лагранжа:
 .
.
Но 
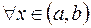 . Поэтому
. Поэтому  , т.е.
, т.е. 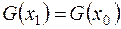 . Считая точку
. Считая точку  фиксированной, а точку
фиксированной, а точку  – произвольной, получим
– произвольной, получим 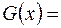 const. Отсюда и следует, что
const. Отсюда и следует, что  , где
, где  – некоторая постоянная.
– некоторая постоянная.
Определение 2. Совокупность всех первообразных для функции 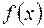 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 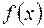 и обозначается символом
и обозначается символом  . В этом обозначении: символ
. В этом обозначении: символ  – знак интеграла,
– знак интеграла, 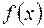 – подынтегральная функция,
– подынтегральная функция,  – подынтегральное выражение, x – переменная интегрирования.
– подынтегральное выражение, x – переменная интегрирования.
Итак,
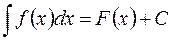 ,
,
где  , а
, а  – некоторая постоянная.
– некоторая постоянная.
Отметим два свойства, непосредственно вытекающие из определения неопределенного интеграла:
 ,
,  .
.
Неопределенный интеграл – это множество функций, и последнее равенство надо понимать так: производная каждой функции из этого множества совпадает с подынтегральной функцией.
С геометрической точки зрения неопределенный интеграл – это семейство кривых, каждая из которых получается путем сдвига одной из кривых вдоль оси  .
.
Примем (пока без доказательства) два полезных свойства первообразных: 1) каждая первообразная нечетной функции – четна; 2) одна из первообразных четной функции – нечетна.
Таблица основных интегралов
Равенство 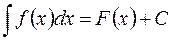 , равносильно равенству
, равносильно равенству  . Поэтому таблица интегралов – это таблица производных, прочитанная справа налево с некоторыми упрощениями и дополнениями.
. Поэтому таблица интегралов – это таблица производных, прочитанная справа налево с некоторыми упрощениями и дополнениями.
1.  ,
,  ;
;  ;
;  .
.
2.  .
.
3. 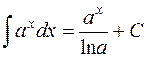 ;
;  .
.
4.  .
.
5. 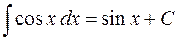 .
.
6. 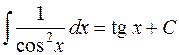 .
.
7.  .
.
8.  .
.
9.  .
.
10. 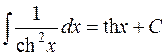 .
.
11.  .
.
12.  ,
,  .
.
13.  ,
,  .
.
14.  ,
,  , – “высокий” логарифм.
, – “высокий” логарифм.
15.  ,
,  , – “длинный” логарифм.
, – “длинный” логарифм.
Всякую формулу интегрирования легко доказать дифференцированием. Например, формула 13:
 .
.
Для простоты пишут  вместо
вместо 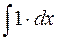 и
и  вместо
вместо  .
.
Замечание. Учитывая свойства аркфункций в формуле 12 вместо  можно писать
можно писать 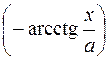 , а в формуле 13 вместо
, а в формуле 13 вместо  писать
писать  .
.
Основные правила интегрирования
I.  .
.
II.  .
.
III. Если 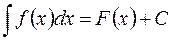 , то
, то  .
.
Неопределенный интеграл – это множество функций и равенства I и II надо понимать как совпадение множеств. Например, равенство I означает следующее: чтобы получить элементы множества  , надо каждый элемент множества
, надо каждый элемент множества  умножить на число
умножить на число  . Правило III можно доказать так:
. Правило III можно доказать так:  . Тогда
. Тогда
 ,
,
т.е. 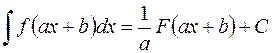 .
.
Отметим, что правило III “работает” только тогда, когда вместо переменной интегрирования  фигурирует линейная функция
фигурирует линейная функция  :
:
 ,
,
но  . Для этогоинтеграла правильный ответ имеет вид:
. Для этогоинтеграла правильный ответ имеет вид: 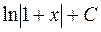 .
.
Замечание. Правило III есть весьма частный случай замены переменной (см. следующий параграф).