Основные методы интегрирования

I Непосредственное интегрирование

Так принято называть вычисление интегралов с помощью таблицы основных интегралов, правил интегрирования и тождественных преобразований подынтегральной функции.

Примеры.

Можно предложить и другой способ:

Ответы по форме различны, но формулы тригонометрии позволяют доказать их тождественность.

3. .

4.Частный случай формулы 14 из §2:

5.Один полезный прием:

II Метод замены переменной

Существуют две реализации этого метода: 1) в качестве новой переменной интегрирования рассматриваем некоторую функцию , которая фигурирует в подынтегральном выражении; 2) переменную интегрирования заменяем специально подобранной функцией .

II.1 Подведение под знак дифференциала

Теорема 1. Пусть известно, что . Тогда, если функция – непрерывно-дифференцируема, то

. (1)

Доказательство. Первое условие теоремы означает, что .

Применяя правило дифференцирования сложной функции, получим

что и доказывает (1).

Чтобы воспользоваться этой теоремой на практике, необходимо вычленить в подынтегральной функции производную некоторой функции, объединить эту производную с дифференциалом переменной интегрирования и сделать замену. После вычисления интеграла вернуться к исходной переменной интегрирования.

Примеры.

Замечание 1. Замену такого типа можно производить и без подведения под знак дифференциала.

Сразу отметим здесь, что такой простой заменой не всегда удается избавить-

ся от иррациональности (попробуйте сами, заменив в числителе на ).

Замечание 2. Приведем две формулы, которые часто встречаются и их

лучше запомнить как табличные.

II.2 Метод подстановки

Теорема 2. Пусть требуется вычислить интеграл и пусть – непрерывно-дифференцируемая функция, имеющая обратную . Тогда, если

, (2)

то

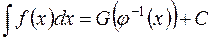. (3)

Доказательство. Равенство (2) означает, что . Тогда

Сравнение начала и конца этой цепочки равенств и доказывает равенство (3).

Пример.

Ответ можно упростить, если учесть формулу синуса двойного угла:

III Интегрирование по частям

Теорема 3. Если и – непрерывно-дифференци-руемые функции, то справедлива формула

(4)

Доказательство вытекает из правила дифференцирования произведения: . Проинтегрируем обе части этого равенства и учтем одно из свойств неопределенного интеграла:

отсюда и следует формула интегрирования по частям (3).

При практическом применении этого метода подынтегральное выражение надо разбить в произведение таким образом, чтобы функция вычислялась просто, а интеграл в правой части (4) был бы проще исходного.

Примеры.

10.

Замечание 3. Если при вычислении интеграла 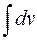взять другую первообразную, например , получим тот же результат:

Замечание 4. Область применения этого метода в основном исчерпывается интегралами вида , где – многочлен, а – это: 1) показательные, тригонометрические 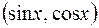и гипербо-лические функции; 2) логарифмические и обратные тригонометрические функции. При этом в качестве в случае 1) берем многочлен, а в случае 2)– логарифмы и аркфункции. Отметим, что в случае 2) «многочлен» может содержать степени переменной с ненатуральными показателями.