I Линейные и дробно-линейные иррациональности
Пусть  – линейная или дробно-линейная функция. Интеграл вида
– линейная или дробно-линейная функция. Интеграл вида  рационализируется подстановкой
рационализируется подстановкой  , где
, где  , так что числа
, так что числа  – целые. Например, если
– целые. Например, если  , то
, то 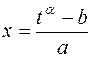 ,
, 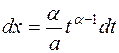 и
и  , где
, где  – некоторая ра-циональная функция.
– некоторая ра-циональная функция.
Аналогично нетрудно показать (рекомендуем сделать это!), что если  , то
, то  и
и 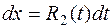 и интеграл
и интеграл  снова рационализируется.
снова рационализируется.
Пример 1.

 .
.
II Квадратичные иррациональности: частный случай
В этой части параграфа рассмотрим интегралы вида  и
и  . В этих интегралах удается избавиться от иррациональности с помощью тригонометрических или гиперболических подстановок, после чего рационализировать интеграл подстановками, рассмотренными в предыдущем параграфе.
. В этих интегралах удается избавиться от иррациональности с помощью тригонометрических или гиперболических подстановок, после чего рационализировать интеграл подстановками, рассмотренными в предыдущем параграфе.
II.1 
 .
.
С тем же успехом можно взять и  ,
,  .
.
II.2
a) 
 ;
;
b) 
 .
.
II.3
a) 
 ;
;
b) 
 .
.
Относительно интеграла 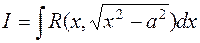 необходимо сделать следующее замечание. Область определения радикала
необходимо сделать следующее замечание. Область определения радикала  состоит из 2-х частей:
состоит из 2-х частей:  . Рассмотренные выше замены справедливы лишь для
. Рассмотренные выше замены справедливы лишь для  . Для
. Для  тригонометрическая замена та же, но
тригонометрическая замена та же, но  и
и  , а гиперболическая замена имеет вид
, а гиперболическая замена имеет вид  В случае четной или нечетной подынтегральной функции можно пользоваться соответствующими свойствами первообразных (см. §1) и не рассматривать отдельно случай
В случае четной или нечетной подынтегральной функции можно пользоваться соответствующими свойствами первообразных (см. §1) и не рассматривать отдельно случай  .
.
Примеры.
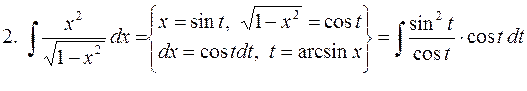

3. 


Если учесть, что 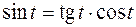 , то ответ можно упростить
, то ответ можно упростить
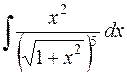
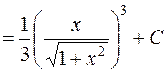 .
.
4.  . Здесь тригонометрическая замена приведет к сложно-му интегралу
. Здесь тригонометрическая замена приведет к сложно-му интегралу  , поэтому лучше применить гиперболическую подстановку:
, поэтому лучше применить гиперболическую подстановку: 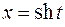 ,
,  ,
,  . Имеем
. Имеем

 .
.
Здесь на последнем шаге использована формула для  и выражение
и выражение  через логарифм.
через логарифм.
5. 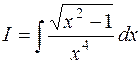 .
.
Для  сделаем замену
сделаем замену  ,
,  , тогда
, тогда  ,
, 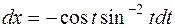 ,
,  и получим
и получим

 .
.
Подынтегральная функция – четная, а полученная первообразная нечетная, значит результат справедлив и для  .
.
III Квадратичные иррациональности: общий случай,
Подстановки Эйлера
Интеграл вида  выделением полного квадрата в подкоренном выражении и соответствующей заменой переменной можно свести к одному из интегралов, рассмотренных ранее.
выделением полного квадрата в подкоренном выражении и соответствующей заменой переменной можно свести к одному из интегралов, рассмотренных ранее.
Однако, существуют и прямые способы рационализации интеграла – это так называемые подстановки Эйлера. Новая переменная интегрирования  вводится такими соотношениями:
вводится такими соотношениями:
1) если  , то
, то  ;
;
2) если 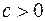 , то
, то  ;
;
3) если  , то
, то  , где
, где  – один из корней квадратного трехчлена.
– один из корней квадратного трехчлена.
Возводя эти соотношения в квадрат и упрощая, можно убедиться в том, что  ,
,  и радикал
и радикал  выражается через
выражается через  рациональным образом. Следовательно, данный интеграл рационализируется.
рациональным образом. Следовательно, данный интеграл рационализируется.
Предлагается студентам самостоятельно произвести все необходимые преобразования и применить эти подстановки к вычислению интегралов:
 ,
,  ,
,  .
.
IV Интегрирование биномиальных дифференциалов:
Подстановки Чебышева
Биномиальным дифференциалом называют выражение вида  , где
, где  ,
,  – действительные числа, а показатели степени
– действительные числа, а показатели степени  ,
,  ,
,  – рациональные числа.
– рациональные числа.
Выясним случаи, когда подобные выражения рационализируются.
IV.1  . Этот случай соответствует ситуации, рассмотренной в пункте I. Действительно,
. Этот случай соответствует ситуации, рассмотренной в пункте I. Действительно,

и интеграл рационализируется подстановкой  , где
, где  .
.
IV.2 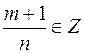 . Рассмотрим подстановку
. Рассмотрим подстановку  , где
, где  – знаменатель дроби
– знаменатель дроби  , так что
, так что  . Тогда
. Тогда  ,
,  и
и

 .
.
IV.3  . Предлагается подстановка
. Предлагается подстановка  , где
, где  – знаменатель дроби
– знаменатель дроби  . Докажите самостоятельно, что и в этом случае, интеграл рационализируется.
. Докажите самостоятельно, что и в этом случае, интеграл рационализируется.
Эти три случая интегрируемости биномиальных дифференциалов в элементарных функциях были известны еще в XVII веке. Однако, лишь в XIX веке Чебышев доказал, что других случаев нет.
Пример 6.  .
.
Здесь 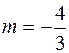 ,
,  и
и  ; так как
; так как 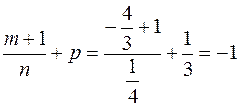 , то имеем случай третьей подстановки Чебышева. Итак,
, то имеем случай третьей подстановки Чебышева. Итак,
 или
или  .
.
Находим отсюда  и
и  :
:
 ,
,  ,
,  ,
,  .
.
Кроме того, 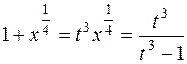 . Имеем для интеграла:
. Имеем для интеграла:
 .
.
Замечание к теме
В первом семестре мы рассмотрели многообразие функций, к которым в первую очередь применяются методы математического анализа – это элементарные функции. Нетрудно убедиться, что операция дифференцирования не выводит нас за пределы этого многообразия. Иначе обстоит дело с обратной операцией – интегрированием. Очень часто оказывается, что первообразная элементарной функции сама не является элементарной. К числу таких заведомо не выражающихся в конечном виде интегралов относятся, например,
 ,
,  ,
, 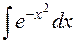
Важно подчеркнуть, что все эти интегралы не только реально существуют, но и играют большую роль как в самом математическом анализе, так и в его приложениях.