Выражений
В предыдущем параграфе мы определили рациональную функцию 
как отношение двух многочленов. Имеется и другое, равносильное, определение, пригодное для функций любого числа переменных.
Функция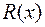 
, 
, 
и т.п. называется рациональной функцией своих аргументов, если над этими аргументами производятся, лишь арифметические операции.
Так запись 
означаем функцию, в которой над 
и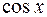 
проводятся только операции сложения, вычитания, умножения и деления.
Нетрудно заметить, что класс всех рациональных функций замкнут относительно арифметических операций, суперпозиции и операции дифференцирования.
I Интегралы вида 
Рационализируются так называемой универсальной тригонометрической подстановкой (УТП) 
. Тогда, как известно из тригонометрии,
;
аналогично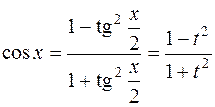 
;
кроме того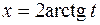 
и 
.
Таким образом, данный интеграл сводится к
,
где 
– некоторая рациональная функция переменной 
.
Пример 1.
.
Рассмотренная подстановка рационализирует всякий интеграл вида 
(потому она и называется универсальной). Однако на практике эта подстановка часто приводит к слишком сложным рациональным функциям. Поэтому полезно знать и другие подстановки, которые в некоторых случаях быстрее приводят к цели.
II Интегралы вида 
Рационализируется так называемой полууниверсальной тригоно-метрической подстановкой 
. Действительно, 
(для аргумента синуса 
аргумент тангенса является половинным);
, 
,
, 
.
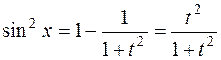Пример 2. 
.
III Интегралы вида 
и 
Подведение под знак дифференциала и соответствующая замена рационализирует эти интегралы.
Пример 3.
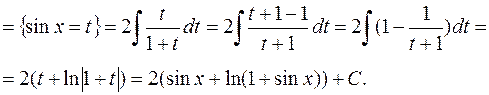
IV Интегралы вида 
Способ преобразования подынтегрального выражения зависит от четности показателей степени.
|
|
IV.1 Хотя бы одно из чисел m, n – нечетное
подстановка 
рационализирует интеграл. Аналогично и для случая 
.
Примеры. 4. 
.
= 
5. 
= 
.
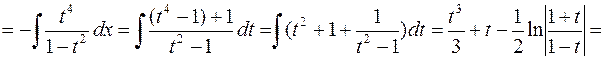
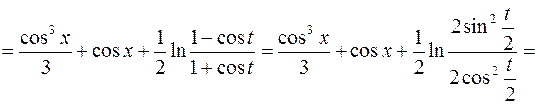
IV.2 Оба числа m и n – четные положительные
В этом случае для преобразования подынтегральной функции используют формулы понижения степени:
, 
.
При этом выражения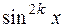 
, 
сводится к сумме членов вида 
. Члены, у которых показатель степени p – нечетный, интегрируются по способу, рассмотренному в пункте IV.1. К остальным членам снова применяют формулу понижения степени, переходя к 
и так далее.
Пример 6. 
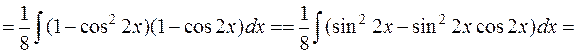
IV.3 Оба числа m и n – четные, хотя бы одно отрицательное
В этом случае применима полу универсальная подстановка, хотя возможны и более простые преобразования с использованием основного тригонометрического тождества. Покажем на примерах
Примеры.
7. 
.
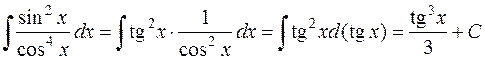8. 
.
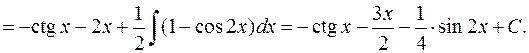9. 
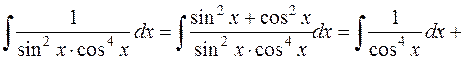
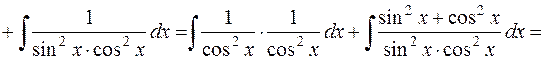
Замечание 1. Для интегралов вида 
можно получать рекуррентные формулы. Например,
= 
.
Здесь первый интеграл – это 
, а ко второму применим интегри-рование по частям, положив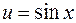 
, 
. Тогда
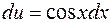и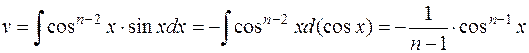 
.
Итак, имеем:
,
.
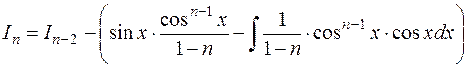Отсюда и получаем рекуррентную формулу
, 
.
Эта формула позволит любой интеграл вида 
, , свести к табличному:
к 
, если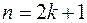 
, или же к 
, если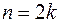 
.
Рекомендуем студентам самим получить рекуррентные формулы для интегралов
, 
, 
.
В двух последних не забудьте, что 
.
Замечание 2. Интегралы вида 
и т.п., вычисляются с использованием формул преобразования произведений тригономет-рических функций в суммы (разности). Например,
.
V Интегралы вида 
Для гиперболических функций имеются разнообразные формулы, аналогичные формулам тригонометрии. Приведем некоторые из них:
|
|
1) основное тождество – 
;
2) формулы двойных углов –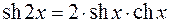 
; 
;
3) формулы понижения степени – 
, 
.
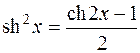Пользуясь этими формулами нетрудно рационализировать любой интеграл вида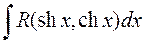 
. Однако, на практике иногда проще выразить гиперболические функции через показательную функцию
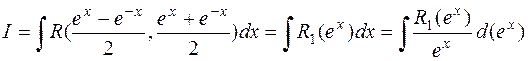
и рационализировать интеграл подстановкой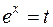 
:
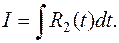
Примеры.
10. 
.
11. 
.