Сформулируем (без доказательств) две теоремы алгебры, которые позволяют свести интегрирование правильных дробей к интегрированию простейших.
Теорема 1. Всякий многочлен с действительными коэффициентами можно разложить единственным образом на множители двух типов: а) ли-нейные 
, б) квадратичные 
, где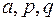 
– действи-тельные числа. Эти множители могут быть простыми, если 
, и крат-ными, если 
.
Отметим, что линейные множители соответствуют действительным корням многочлена, а квадратичные – парам комплексных сопряженных корней.
Теорема 2. Всякую правильную рациональную дробь можно разложить на сумму простейших дробей; при этом:
a) линейному простому множителю в разложении знаменателя дроби на множители соответствует дробь 1го типа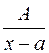 
;
b) линейному кратному множителю 
соответствует сумма дробей 1го и 2го типов вида
;
c) квадратичному простому множителю 
соответствует дробь 3го типа 
;
d) квадратичному кратному множителю 
соот-ветствует сумма дробей 3го и 4го типа вида
.
Здесь 
, 
, 
– некоторые действительные числа, часть из которых может быть равна 0. Указанное разложение единственное (с точностью до порядка слагаемых).
Можно предложить следующий алгоритм разложения правильной дроби на простейшие слагаемые:
1) в соответствии с разложением знаменателя дроби на множители выписываем формальное разложение дроби на простейшие слагаемые с неизвестными коэффициентами;
2) приводим выписанную сумму дробей к общему знаменателю;
3) приравниваем числитель дроби, полученной в пункте 2), числителю исходной дроби;
4) равенство (тождественное!) многочленов, полученное в пункте 3) позволит нам найти неизвестные коэффициенты либо методом неопределенных коэффициентов (т.е. приравнивая коэффициенты, стоящие при равных степенях х) либо методом частных значений (т.е. придавая переменной х конкретные – “ удобные ” – значения).
Замечание. Метод частных значений особенно удобен в случае прос-тых действительных корней знаменателя разлагаемой дроби. Можно ком-бинировать оба метода определения неизвестных коэффициентов.
Примеры. 1. Разложить на простейшие слагаемые дробь
1й шаг: пишем формальное разложение
2й шаг: приводим сумму дробей к общему знаменателю
3й шаг: приравниваем числители
4й шаг: метод неопределенных коэффициентов дает систему уравнений
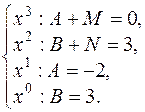
Отсюда: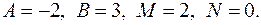 
Искомое разложение имеет вид
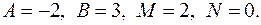
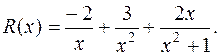
Теперь, если понадобится, легко найти интеграл 
2. Вычислить 
.
Имеем 
Отсюда следует тождество
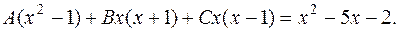
Для определения коэффициентов положим в этом тождестве последовательно 
. Сразу получим: 
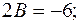
, т.е. 
, 
, 
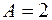. Окончательно имеем:
3. 
Разложение на простейшие дроби здесь достигается путем незамысловатых преобразований:
Искомый интеграл равен 
В заключение сформулируем основной результат данного параграфа: интегралы от рациональный функций выражаются в конечном виде с помощью рациональных функций, логарифмов и артангенсов. Иными словами, всякая рациональная функция интегрируется в элементарных функциях.
В связи с этим интегралы от иррациональных и трансцендентных выражений стараются специально подобранными подстановками рационализировать, т.е. свести к интегралам от рациональных функций. Этим подстановкам и будут посвящены следующие параграфы.