Абсолютной (относительно земной поверхности) скоростью судна при плавании с учетом течения является результат геометрического сложения скорости перемещения судна относительно водной среды и вектора скорости течения.
При плавании с учетом постоянного течения решаются прямая и обратная задачи на прокладку пути судна.
Прямая задача. Найти линию пути ПУb, если известны ИК (КК), V л, направление течения (Кт) и его скорость (V т).
Решение:
От начальной точки (рис. 4.1) по линии ИК отложим в масштабе карты вектор скорости судна V л.
От конца этого отрезка отложим в том же масштабе вектор скорости течения V т.
Прямая, проведенная между начальной и конечной точками вектора течения, называется линией пути ПУb.
Угол между направлением истинного меридиана и линией пути называется путевым углом на течении ПУb, а угол между линией ИК и линией пути – углом сноса течением b (поправка на течение):
ПУb = ИК + b.

Рис. 4.1
Обратная задача. Найти КК (ИК), когда задан ПУb и известны V л, Кт, V т (рис. 4.2).
Решение:
От начальной точки проведем линию пути ПУb.
От этой же точки отложим вектор скорости течения V т.
От конечной точки вектора скорости течения раствором измерителя, равным скорости судна V л, сделаем засечку на линии пути ПУb
Проведем из начальной точки 0 прямую, параллельную прямой АВ, и получим линию ИК.
Рассчитаем КК = ИК – DK.
Угол сноса течением (поправка на течение) определим по формуле
b = ПУb – ИК.
Формулы алгебраические, поэтому знак угла b определяется следующим образом: если течение направлено в левый борт, то величина угла записывается со знаком "+", если в правый – со знаком "–".

Рис. 4.2
При оценке точности счислимого места судна при плавании на постоянном течении погрешности в элементах течения будут такими же, как погрешности счисления на отдельном курсе. Применяем следующую формулу:
 ,
,
где М т – погрешность счисления из-за погрешностей в элементах течения.
Величина погрешности счисления М т из-за погрешностей в элементах течения будет легко определена, если мы условно сделаем замену: Кт = К, V т = V 0. Тогда
 .
.
Таким образом, погрешность счисления прямо пропорциональна времени плавания, она увеличивается также и при увеличении скорости течения.
Если плавание на постоянном течении осуществляется по одному курсу, то погрешность счисления определяется по формуле
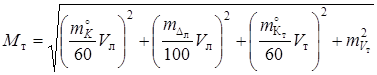 .
.
Можно указать ориентировочные максимальные значения погрешностей для течений в открытом море: скорости – до 0,5 уз, направления – до 30°.
Пример решения задачи
Исходные данные указаны в таблице.
| Номер п/п | Судно по счислению прошло | Расстояние |
| за 2 ч 07 мин по ИК1 = 305,0° | S 1 = 27 миль | |
| за 3 ч 48 мин по ИК2 = 253,0º | S 2 = 54 мили | |
| за 1 ч 55 мин по ИК3 = 90,0º | S 3 = 18 миль |
При переходе учитывалось действие постоянного течения на SE, V т = 2,2 уз.
Вычислить радиус круга погрешностей конечной счислимой точки, если m к = ±1,5°, m Dл = ±1,8 %, mКт = ±18º, mVт = ±0,3 уз.
Решение:
Используя табл. 4.1, по аргументам m к и m Dл определяем Мn '= 0,308 мили на каждые 10 миль плавания, а затем рассчитываем радиусы погрешности:
М 1 = 0,308 · 2,7 = 0,833 мили,
М 2 = 0,308 · 5,4 = 1,663 мили,
М 3 = 0,308 · 1,8 = 0,555 мили.
Рассчитываем М т:
 (02h07m + 03h48m + 01h55m) ×
(02h07m + 03h48m + 01h55m) ×
×  миль.
миль.
Определяем М с

 миль.
миль.
Это и будет радиус круга погрешностей счислимой точки. Внутри такого круга с вероятностью 63 ¸ 68 % находится судно. Образец заполнения расчетной таблицы и оформления прокладки графического счисления пути судна с учетом течения приведен в приложении 10.