При вычерчивании деталей, построении разверток поверхностей вам приходится выполнять различные геометрические построения, например делить на равные части отрезки и окружности, строить углы, выполнять сопряжения и др.
Многие из этих построений вам уже известны из уроков геометрии и других предметов, поэтому здесь они не рассматриваются. Рациональные приемы построения углов с помощью чертежных инструментов приведены на форзаце в конце книги.
15.1. Анализ графического состава изображений. Прежде чем приступить к выполнению чертежа, надо определить, какие геометрические построения потребуется применить в данном случае. Рассмотрим пример.
На рисунке 123, а приведены три проекции опоры, наглядное изображение которой дано на рисунке 74, а. Чтобы начертить этот предмет, надо выполнить ряд графических построений:
1) провести параллельные прямые;
2) построить сопряжение (скругление) двух параллельных прямых дугой заданного радиуса (рис. 123, б);
3) провести три концентрические окружности (рис. 123, в);
4) вычертить трапецию (рис. 123, г).
Рис. 123.Анализ графического состава изображений
|
Расчленение процесса выполнения чертежа на отдельные графические операции называется анализом графического состава изображений.
| © |
Определение графических операций, из которых слагается построение чертежа, облегчает его выполнение.
1. Какие геометрические построения вам известны?
2. Как называется расчленение процесса выполнения чертежа на отдельные графические операции?
3. Для чего нужен анализ графического состава изображений?
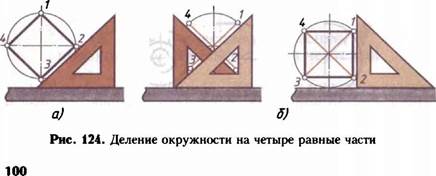
15.2. Деление окружности на равные части. Многие детали имеют равномерно расположенные по окружности элементы, например отверстия, спицы и т. д. Поэтому возникает необходимость делить окружности на равные части.
Деление окружности на четыре равные части. Чтобы разделить окружность на четыре равные части, нужно провести два взаимно перпендикулярных диаметра.
Два случая таких построений показаны на рисунке 124. На рисунке 124, а диаметры проведены по линейке и катету равнобедренного угольника, а стороны вписанного квадрата — по его гипотенузе. На рисунке 124, 6, наоборот, диаметры проведены по гипотенузе угольника, а стороны квадрата — по линейке и катету угольника.
Деление окружности на восемь равных частей. Чтобы разделить окружность на восемь равных частей, достаточно провести две пары диаметров, т. е. объединить оба случая построения квадрата (см. рис. 124). Одну пару взаим-
|
но перпендикулярных диаметров строят по линейке и катету, другую — по гипотенузе угольника (рис. 125).
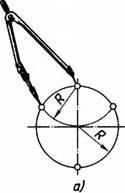
Деление окружности на три равные части. Поставив опорную ножку циркуля в конце диаметра (рис. 126, а), описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деление. Третье деление находится на противоположном конце диаметра.
Ту же задачу можно решить с помощью линейки и угольника с углами 30, 60 и 90°. Для этого устанавливают угольник большим катетом параллельно вертикальному диаметру. Вдоль гипотенузы из точки 1 (конца диаметра) проводят хорду, получают второе деление (рис. 126, б). Повернув угольник и проведя вторую хорду, получают третье деление (рис. 12(1, в)
Соединив точки 2 и 3 отрезком прямой, получают раштетп ронний треугольник.
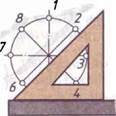Рис. 125. Деление окружности на восемь равных частей
|
Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности, так как сторона шестиугольника равна радиусу описанной окружности. Из противоположных концов одного из диаметров окружности (например, точек / и 4, рис. 127, а) описывают дуги. Точки 1, 2, 3, 4, 5, 6 делят окружность на равные части. Соединив их отрезками прямых, получают правильный шестиугольник (рис. 127, б).
|
Рис. 126. Деление окружности на тр! равные части: с помощью циркуля; б, в— с помощью угольника и линейки
|
| б) |
| б) |
a) '<5 ~Т~"5' б)
Рис. 127. Деление окружности на шесть равных частей с помощью циркуля
|
|
I I
а) б) 6)
Рис. 128. Деление окружности на шесть равных частей с помощью угольника и линейки
Ту же задачу можно выполнить при помощи линейки и угольника с углами 30 и 60° (рис. 128).
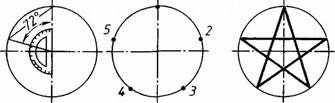
Деление окружности на пять равных частей. Пятой части окружности соответствует центральный угол в 72° (360°: 5 = 72°). Этот угол можно построить при помощи транспортира (рис. 129, а).
На рисунке 129, б показано вычерчивание пятиконечной звезды.
а) б)
Рис. 129. Деление окружности на пять равных частей
|
40. Постройте с помощью линейки и угольника правильный шестиугольник, две вершины которого лежат на горизонтальной центровой линии. Выполните то же построение с помощью циркуля.
15.3. Сопряжения. У шаблона на рисунке 130 углы скруглены. Прямые линии плавно переходят в кривые. Такой же плавный переход может быть между прямыми или между двумя окружностями.
Плавный переход одной линии в другую называют сопряжением.
Для построения сопряжений надо найти центры, из которых проводят душ, т. е. центры сопряжений. Надо найти также точки, в которых одна линия переходит в другую, т. е. точки сопряжений.
Таким образом, для построения любого сопряжения надо найти центр сопряжения, точки сопряжений, знать радиус сопряжения.
При построении сопряжений следует иметь в виду, что переход от прямой к окружности будет плавным в том случае, если прямая касается окружности (рис. 131, а). Точка сопряжения лежит на радиусе, перпендикулярном данной прямой.
Переход от одной окружности к другой будет плавным, если окружности касаются. Точка сопряжения находится на прямой, соединяющей их центры (рис. 131, б).
Сопряжение двух прямых дугой заданного радиуса. Даны прямые, составляющие прямой, острый и тупой углы (рис. 132, а) и величина R радиуса дуги сопряжения. Требуется построить сопряжение этих прямых дугой заданного радиуса.
Для всех трех случаев применяют общий способ построения.
1. Находят точку О — центр сопряжения (рис. 132, б). Он должен лежать на расстоянии R от заданных прямых. Очевидно, такому условию удовлетворяет точка пересечения двух прямых, расположенных параллельно заданным на расстоянии R от них. Что-
Рис. 131. Построение сопряжений а) б)
|
| 1 | 0 |
| Т * | |
Рнс. 132. Общий способ построения сопряжений двух пересекающихся прямых
|
| А |
т
бы построить эти прямые, из произвольно выбранных точек каждой заданной прямой проводят перпендикуляры. Откладывают на них длину радиуса R. Через полученные точки проводят прямые, параллельные заданным.
В точке пересечения этих прямых находится центр О сопряжения.
2. Находят точки сопряжения (рис. 132, в). Для этого проводят перпендикуляры из центра сопряжения к заданным прямым. Полученные точки являются точками сопряжений.
3 Поставив опорную ножку циркуля в точку О, проводят дугу заданного радиуса R между точками сопряжении (рис. 132, в).
Сопряжение окружности и прямой дугой заданного радиуса. Даны окружность радиуса R, отрезок АВ и радиус дуги сопряжения Rt (рис. 133).
Построение выполняют так:
1. Для нахождения центра сопряжения из точки О окружности проводят дугу вспомогательной окружности радиуса R +
На расстоянии Z?j от прямой АВ проводят парал лельную ей прямую до пересечения с дугой /? + /?! Точка О) будет центром сопряжения.
2 Соединив прямой точки О и О), т. е. центры окружности и сопрягающей дуги, получают точку со пряжения М. Проведя из точки 0( перпендикуляр к прямой АВ, определяют вторую точку сопряжения N.
3. Соединив дугой точки М и N сопряжения, получают плавный переход от окружности к прямой.
15.4. Применение геометрических построений на практике. Чтобы изготовить из металлического листа деталь, например шаблон, изображенный на рисунке 130, надо прежде очертить на металле его контур, т. е. сделать разметку. Между выполнением чертежа и разметкой много общего
При выполнении чертежа или разметки надо определить, какие геометрические построения следует при этом применить, т. е. провести анализ графического состава изображений (см. 15.1). Слева на рисунке 134 показаны эти построения.
Рис. 133. Построение сопряжения дуги окружности и прямой
|
В результате анализа устанавливаем, что вычерчивание контура шаблона слагается в основном из построения угла 60° и сопряжений острого и тупого углов дугами заданных радиусов.
Рис. 134. Анализ контура изображения детали
|
|
| / d | |
| /т | |
| 4 \ | |
| ч | V |
| { | } \ |
| о RU —ч | |
| k | \ сэ £ А /к |
| 100 |
| Рис. 135.Последовательность построения чертежа шаблона |
| б) |
| д) |
и
Какова последовательность разметки шаблона? Можно ли ее начинать с построения сопряжений? Очевидно, нет.
Правильная последовательность построения чертежа показана на рисунке 135. Сначала проводят те линии чертежа, положение которых определяется заданными размерами и не требует дополнительных построений, а затем строят сопряжения.
| 1. Какие углы можно построить с помощью угольников? 2. Чему равен раствор циркуля при делении окружности на шесть равных частей, на три равные части? 3. Что называется сопряжением? 4. Назовите элементы, обязательные в любом сопряжении. 5. Какие построения встретятся вам при выполнении чертежа детали, представленной на рисунке 136? 41. По аксонометрической проекции (рис. 137) выполните чертеж детали. |
Таким образом, построение ведут в такой последовательности. Вначале проводят осевую линию и прямую, на которой лежит основание шаблона (рис. 135, а). На этой прямой вправо и влево от осевой линии откладывают половину длины основания, т. е. по 50 мм. Затем строят углы 60° и проводят прямую параллельно основанию на расстоянии 50 мм от него (рис. 135, б). После этого находят центры и точки сопряжений (рис. 135, в и г). В заключение проводят дуги сопряжений. Обводят видимый контур и наносят размеры (рис. 135, д).
Ф20
Рис. 136. Задание для Рис. 137. Задание для упражнений
упражнений
|
|
| © |
ГРАФИЧЕСКАЯ РАБОТА № 6
|