Проекции вершин, ребер и граней предмета

12.1. Как изображают элементы предметов. Любая точка или отрезок на изображении предмета является проекцией того или иного элемента: вершины, ребра, грани, кривой поверхно­сти и т. п. (рис. 85). Поэтому изображение любого предмета сво­дится к изображению его вершины, ребер, граней и кривых по­верхностей.

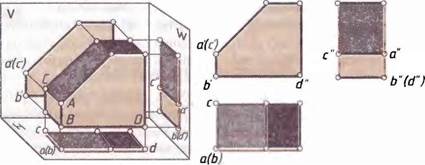
Рассмотрим этот процесс на примере построения прямо­угольных проекций предмета (рис. 86).

Расположим предмет в пространстве так, чтобы каждая из двух параллельных между собой граней была параллельна од­ной из плоскостей проекций. Тогда эти грани изобразятся на соответствующих плоскостях проекций без искажения.

Проведем через вершины предмета проецирующие лучи, перпендикулярные плоскостям проекций, и отметим точки пе­ресечения их с плоскостями V, Н и W.

б)

Предмет так расположен относительно плоскостей проекций, что на одном проецирующем луче оказалось по две вершины, по­этому их проекции слились в одну точку. Так, вершины А и В
лежат на одном луче, перпендику лярном горизонтальной плоскости проекций Н. Их горизонтальные проекции а и b совпали. Вершины А и С лежат на одном луче, прое­цирующем эти точки на фронталь­ную плоскость проекций. Их фрон­тальные проекции а! и с' также со­впали. На профильной плоскости проекций W в одну точку (Ь" и d") спр(х>цировались вершины В и D.

Из двух совпадающих на изо­бражении точек одна является изо­бражением видимой вершины, дру­гая — закрытой (невидимой). На горизонтальной проекции будет ви­дима та вершина, которая расположена в пространстве выше. Так, вершина А видима, вершина В невидима. На фронтальной проек­ции видимой будет та вершина, которая находится ближе к нам. Отсюда а' — изображение видимой вершины А, с' —изображение невидимой вершины С, она закрывается при проецировании вер­шиной Л. На изображении обозначение проекций невидимых точек берут иногда в скобки.

Соединив попарно точки на фронтальной, горизонтальной и профильной проекциях, получим изображения ребер предмета. Например, ас — горизонтальная проекция ребра АС, а'Ь' — фрон­тальная проекция ребра АВ,

Ребра

Вершины

поверхность

Рис. 85.Элементы поверхности предмета

На рисунке 86 видно, что если ребро параллельно плоскости

 

проекций, то оно на этой плоскости изображается без искажения, или, как говорят, в истинную (натуральную) величину. В этом случае проекция ребра и само ребро равны между собой. Напри­мер, проекция а'Ь' — истинная величина ребра АВ на фронталь­ной, а проекция а"Ь" — на профильной плоскости проекций.

Если ребро перпендикулярно плоскости проекций, оно проецируется на нее в точку. Так, на фронтальную плоскость проекций в точку спроецировалось ребро АС, на горизонталь­ную плоскость — ребро АВ, на профильную — ребро BD и т. д.

Построив проекции ребер, видим, что на изображении они ограничивают проекции граней. Как и ребро, грань, параллель­ная плоскости проекций, проецируется на нее без искажения. Например, на профильную плоскость проекций без искажения спроецировалась грань, в которой лежат точки А, В и С. На горизонтальную плоскость проекций спроецировались без ис­кажения нижняя и верхняя грани и т. д. Найдите эти грани на чертеже предмета в системе прямоугольных проекций.

Если грань перпендикулярна плоскости проекций, она прое­цируется на нее в отрезок прямой.

Таким образом, каждый отрезок прямой на изображении — это проекция ребра или проекция плоскости, перпендикуляр­ной плоскости проекций. Ребра и грани предмета, наклоненные к плоскости проекций, проецируются на нее с искажением. Най­дите такие ребра и грань на рисунке 86.

Строя чертеж, надо четко представлять, как изобразится на нем каждая вершина, ребро и грань предмета. Читая чертеж, надо представить, изображение какой части предмета скрыто за каждой точкой, отрезком или фигурой.

©

Следует помнить, что каждый вид — это изображение всего предмета, а не одной его стороны. Разница заключается лишь в том, что одни грани спроецируются в истинную фигуру, дру­гие — в отрезки прямых.

 

 

5)

а)

 

Рис. 87. Задания для упражнений

21. На рисунке 87, а даны наглядное изображение и три проекции детали. На чертеже показаны проекции точки А, яв­ляющейся одной из вершин детали.

1) Как называются заданные проекции детали?

2) Перечертите в рабочую тетрадь или перенесите на каль­ку проекции детали^[4]. Нанесите на них проекции точек В и С.

3) Выделите одним цветом на проекциях ребро ВС. Укажи­те, на какие плоскости проекций это ребро спроецировалось в истинную величину.

4) Выделите (раскрасьте) одним цветом на всех проекциях ту грань детали, которая не параллельна ни одной из плоскос­тей проекций.

22. На рисунке 87, б дано изображение детали.

1) Сосчитайте, сколько вершин имеет изображенный пред­мет. Если вы затрудняетесь сделать подсчет, обозначьте вер­шины буквами.

2) Сосчитайте, сколько ребер и граней у предмета.

4»

3) Сколько у предмета ребер и граней, параллельных гори­зонтальной плоскости проекций? Покажите их на проекциях.

4) Сколько ребер и граней, перпендикулярных горизон­тальной плоскости проекций? Покажите их на изображении Если вы затрудняетесь решить задачу, сделайте предмет из какого-либо материала и поставьте его, как на рисунке 87. Пусть плоскость стола — это горизонтальная плоскость проек­ций. Попробуйте теперь, сравнивая изображение и предмет, правильно ответить на вопросы.

Рис. 88.Изображение элементов поверхности детали

 

23. Нэ рисунке 88 грани предмета выделены цветом. Обо­значьте вершины буквами или цифрами. Проанализируйте, как расположены грани предмета относительно плоскостей проекций. Ответ запишите в рабочей тетради.

24. Перечертите или перенесите на кальку рисунок 89 и вы­делите на всех проекциях соответствующие грани тем же цве­том, что и на наглядных изображениях.

25. На рисунке 90 даны изображения трех предметов. Про­екции их граней обозначены буквами. Напишите, как располо­жены в каждом случае относительно фронтальной плоскости проекций эти грани. Пример записи: А — параллельно, Б — перпендикулярно, В — наклонно.

 

		л	и				г
	—i—

А

 

a)

L

 

jO

IQ Ш

ВД

S)

 

 

 

12.2. Построение проекций точек на поверхности предмета.

Теперь рассмотрим способы построения проекций точек, ле­жащих на поверхностях предметов.

На рисунке 91 изображена шестиугольная пирамида. На линии, являющейся проекцией ребра, задана фронтальная проекция а' точки А, Как найти ее остальные проекции?

Рассуждают так. Точка находится на ребре предмета. Про­екции точки должны лежать на проекциях этого ребра. Сле­довательно, нужно сначала найти проекции ребра, а затем при помощи линий связи отыскать проекции точки.

Чтобы построить профильную проекцию предмета и, в ча­стности, профильную проекцию ребра, на котором находится точка Л, удобно воспользоваться постоянной прямой. Так на­зывают линию, которую проводят справа от вида сверху под углом 45° к рамке чертежа (рис. 91). Линии связи, идущие от вида сверху, доводят до постоянной прямой. Из точек их пе­ресечения проводят перпендикуляры к горизонтальной пря­мой и строят профильную проекцию.

Расположение постоянной прямой определяет место строя­щегося вида (рис. 91). Но если три вида уже построены, как на рисунке 92, а, нужно найти точку, через которую пройдет посто­янная прямая. Для этого достаточно продолжить до взаимного пе-

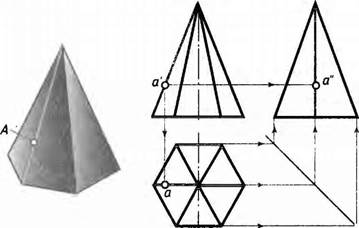Рис. 91. Построение проекции точки, лежащей на ребре пирамиды

Ч

у—	—ч.

	ч
	I
«1
	[К

<33

а) 5)

Рис. 92. Построение постоянной прямой

ресечения горизонтальную и профильную проекции оси симмет­рии. Через полученную точку К (рис. 92, б) проводят прямую под углом 45° к осям. Это и будет постоянная прямая.

Если осей симметрии на чертеже нет, то продолжают до пе­ресечения в точке /С, (рис. 92,6) горизонтальную и профильную проекции граней, проецирующихся в виде отрезков прямых. Через точку К\ проводят постоянную прямую.

А теперь вернемся к рисунку 91. Проекции ребра, на кото­ром лежит точка А, выделены коричневым цветом. Горизон­тальная проекция точки А должна лежать на горизонтальной проекции ребра, поэтому проводим из точки а' вертикальную линию связи. В месте ее пересечения с проекцией ребра нахо­дится точка а — горизонтальная проекция точки А.

Профильная проекция а" точки А лежит на профильной проекции ребра. Ее можно определить и как точку пересечения линий связи.

Мы рассмотрели, как находят на чертеже проекции точек, лежащих на ребрах предметов. Однако часто приходится стро­ить проекции точек, лежащих не на ребрах, а на гранях. На­пример, чтобы просверлить в детали отверстие, надо опреде­лить, где находится его центр.

Чтобы по одной проекции точки, лежащей на грани предме­та, найти остальные, нужно прежде всего найти проекции этой грани. Такие упражнения вы уже выполняли (см. рис. 89). За­тем при помощи линий связи надо отыскать проекции точки, которые должны лежать на проекциях грани.

Линию связи сначала проводят к той проекции, на которой грань изображается в виде отрезка прямой.

	С	1'
ьУ				Ь" •
Мм
ь
		о 1		---- X

 

Рис. 93. Построение проекций точки, лежащей на поверхности предмета

На рисунке 93 проекции грани, содержащие проекции точки А, выделены цветом. Точка А задана фронтальной проекцией а'. Горизонтальная проекция а этой точки должна лежать на гори­зонтальной проекции грани. Для ее нахождения проводят вер­тикальную линию связи из точки а'.

Чтобы найти профильную проекцию, нужно из точки а' про­вести горизонтальную линию связи. В месте ее пересечения с

W U _ / /

отрезком прямой — проекцией грани — лежит точка а.

йьа

Чвши

а) 5)

LS.

a b

Рис. 94. Задания для упражнений

Построение проекций точки В, заданной горизонтальной проекцией Ь, также показано линиями связи со стрелками.

26. На рисунке 94, а, б даны чертежи в системе прямоуголь­ных проекций и наглядные изображения предметов. На видах буквами обозначены проекции вершин. Перечертите или пе­ренесите на кальку заданные изображения. Обозначьте бук­вами остальные проекции вершин. Найдите эти вершины на наглядных изображениях и обозначьте их буквами.

27. Перечертите или перенесите на кальку заданные изобра­жения (рис. 95) и постройте недостающие проекции точек, задан­ных на ребрах предмета. Выделите цветом проекции ребер (для каждого ребра свой цвет), содержащих точки. Нанесите точки на аксонометрической проекции и выделите теми же цветами ребра, на которых лежат точки.

j		а;	L

/	\
ч J	/ •ч

Рис. 95. Задание для упражнений Рис. 96. Задание для упражнений

28. Перечертите или пе­ренесите на кальку рисунок 96. Постройте недостаю­щие проекции точек, задан­ных на видимых поверхно­стях предмета. Выделите цветом проекции поверх­ностей, на которых лежат точки (для каждой поверх­ности свой цвет). Выделите поверхности предмета на наглядном изображении теми же цветами, что и на чертеже, и нанесите точки.

29. Перечертите или перенесите на кальку рисунок 97. Постройте недостающие проекции точек и обозначьте их бук­вами. Выделите цветом, как и в предыдущем задании, проек­ции поверхностей, на которых лежат эти точки.

о