Код высшей классификационной 3 глава

Через полученную точку М и центр О окружности проводят прямую до встре­чи с противоположной стороной окружно сти в точке Л'. Точку М соединяют прямой с точкой ^л4. <

Деление отрезка прямой на любое число равных частей. Из любого конца отрезка, например из точки И, проводят под острым углом к нему прямую линию. На ней цир­кулем-измерителем откладывают нужное число равных отрезков произвольной вели чины (рис. 47). Последнюю точку соеди­няют со вторым концом заданного отрезка (с точкой В). Из всех точек деления с по­мощью линейки и угольника проводят пря­мые, параллельные прямой 96, которые и разделят отрезок л4Я на заданное число равных частей.

На рис. 48 показано, как применить это построение для разметки центров отвер­стий, равномерно расположенных на пря мой.

 

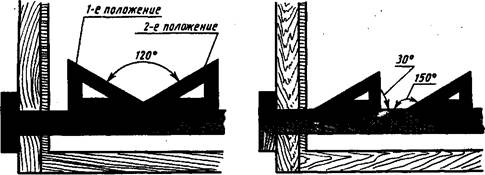
Построение угла 120*

Построение углоб 60 и 120•

Построение углов л /у /У#*

 

Построение углов 15 и 165•

 

/?ОС/7?/7СМлС00 7У</ /УУ

/7СГЯ7/7РМЫ?-»^ А7У*

Рис. 4). Построение острых и тупых углов с помощью рейсшины и угольников

 

В х

Рис. 43. Деление прямого углана три равные части с помощью циркуля

Рис. 47. Деление отрезка на любое число равных частей

Рис. 44. Построение углов, равных дан- Л ному

Рис. 48. Пример применения построений, приведенных на рис. 47

$)2. ДЕЛЕНИЕ ОКРУЖНОСТИ

НА РАВНЫЕ ЧАСТИ

Деление окружности на три равные час­ти. Устанавливают угольник с углами 30 и 60° большим катетом параллельно одной из центровых линий. Вдоль гипоте­нузы из точки / (первое деление) прово­дят хорду (рис. 49, а), получая второе деление — точку 2. Перевернув угольник и проведя вторую хорду, получают третье деление — точку 3 (рис. 49, б). Соединив точки.2 и <? и 3 и / прямыми, получают равносторонний треугольник.

Ту же задачу можно решить с помощью циркуля. Поставив опорную ножку цирку­ля в нижний или верхний конец диаметра (рис. 49, а), описывают дугу, радиус кото­рой равен радиусу окружности. Получают первое и второе деления. Третье деление находится на противоположном конце ди­аметра.

Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу Д окружности. Из концов одного из диаметров окружности (из точек /, описывают дуги (рис. 50, а, б). Точ­ки /2, 3, 4, 5, 6 делят окружность на шесть равных частей. Соединив их прямы­ми, получают правильный шестиугольник (рис. 50, б).

Ту же задачу можно выполнить с по­мощью линейки и угольника с углами 30 и 60° (рис. 51). Гипотенуза угольника при этом должна проходить через центр окружности.

Деление окружности на восемь равных частей. Точки /, 3, 5, 7 лежат на пересече­нии центровых линий с окружностью (рис. 52). Еще четыре точки находят с по­мощью угольника с углами 45°. При полу­чении точек 2, 4, 6, й гипотенуза уголь­ника проходит через центр окружности.

Деление окружности на любое число равных частей. Для деления окружности на любое число равных частей пользуются коэффициентами, приведенными в табл. 3.

Длину? хорды, которую откладывают на заданной окружности, определяют по фор­муле / =-^£де? — длина хорды, <% — диаметр заданной окружности, % — коэф­фициент, определяемый по табл. 3.

Чтобы разделить окружность заданного диаметра 90 мм, например, на)4 частей, поступают следующим образом.

Риг. 49. Деление окружности на три равные части: а. б - с помощью угольника, 6 — с по- мощыоииркуля

 

 

3. Коэффициенты для деления окружностей Число   Число   деле­ Коэффициент А деле- Коэффициент А ний я   ний п     0,86603   0,34202   0,7074 Ю 0,30902   0,58779 Н 0,28)73   0,50000 [2 0,25882   0,43388 [3 0,23932   0,38268 )4 0,22252

 

В первой графе табл. 3 находят число делений я, т. е. 14. Из второй графьлвыпи- сывают коэффициент &, соответствующий числу делений я. В данном случае он ра­вен 0,22252. Диаметр заданной окружно-. сти умножают на коэффициент и получают длину хорды / = а!&=90-0,22252яз ж0,22 мм. Полученную длину хорды от­кладывают циркулем-измерителем [4 раз на заданной окружности.

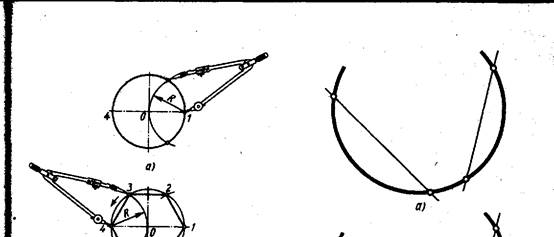
Нахождение центра дуги и определение величины радиуса. Задана дуга окружно­сти, центр и радиус которой неизвестны.

Для их определения нужно провести две непараллельные хорды (рис. 53, а) и вос-

 

Рис. 53. Определение центра дуги

 

ставить перпендикуляры к серединам хорд (рис. 53,6). Центр О дуги находится на пересечении этих перпендикуляров.

Контрольные вопросы

). Что называют анализом графического со­става изображений?

2. Для чего нужен анализ графического со­става изображения?

3. Какими линиями выполняют вспомога­тельные построения?

Задания к §)0 и П

Упражнение 5. С помощью линейки и уголь­ника постройте углы 30, 60,)20, 75, [5 и Ю5°.

Упражнение 6. Разделите отрезок прямой на четыре равные части; на восемь равных частей; на [2 равных частей.

Упражнение 7. Разделите тупой угол на четы­ре равные части.

Упражнение Д. Разделите прямой угол на три равные части с помощью циркуля и линейки. Постройте угол 30°. Разделите окружность на три равные части.

Рис. 50. Деление окружности на шесть равных частей с помощью циркуля

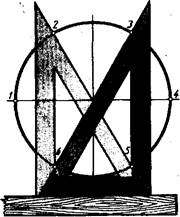Рис. 5!. Деление окружности на шесть равных частей с помощью угольника

Рис. 52. Деление окружности на во­семь равных частей с помощью угольника

— 33 —

2 Техническое черчение

Упражнение У. С помощью угольника и ли­нейки разделите окружность на шесть равных частей (на)2). То же самое сделайте с по­мощью ииркуля.

Рис. 54. Заданно для упражнений

 

УяряжАмяие /0. Разделите окружность на восемь ' равных частей наиболее рациональным способом.

Уяряамюмиб //. Подсчитайте, чему равна длина хорды при делении окружности диаметра)00 мм на пять равных частей: окружности диаметра)20 мм на)4 равных частей: окруж­ности диаметра 200 мм на П равных частей.

Уяряжяммм /2. Вычертите чертеж угольника (рис. 54).

Уяражяемиб /3. Выполните один из чертежей прокладок, приведенных- на рис. 55, а — а.

Ф80

 

а)

 

Рис. 55. Задания для упражнений — 34 —

Рис. 55. Продолжение

 

$)3. СОПРЯЖЕНИЯ

При выполнении машиностроительных чертежей, а также при разметке заготовок деталей на производстве часто приходится плавно соединять прямые линии с дугами окружностей или дугу окружности с дуга­ми других, окружностей, т. е. выполнять сопряжение.

Сопряжением называют плавный переход прямой в дугу окружности или одной дуги в другую.

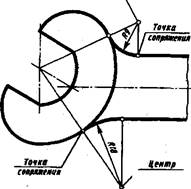
Рис. 56. Элементы сопряжений

'сопрлтшя

Для построения сопряжений надо знать величину радиуса сопряжений, найти цен­тры, из которых проводят дуги, т. е. ц е н- тры сопряжений (рис. 56). Затем нужно найти точки, в которых одна линия переходит в другую, т. е. точки со­пряжений. При построении чертежа сопрягающиеся линии нужно доводить Дняяр гмрмжмми точно до этих точек. Точка сопряжения дуги окружности и прямой лежит на пер­пендикуляре, опущенном из центра дуги на сопрягаемую прямую (рис. 57, а), или на линии, соединяющей центры сопрягае­мых дуг (рис. 57,6). Следовательно, для построения любого сопряжения дугой за­данного радиуса нужно найти центр сопряжения и точку (точки) сопряжения.

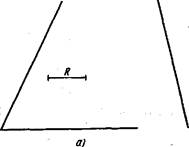
Сопряжение двух, пересекающихся пря­мых дугой заданного радиуса. Даны пе - ресекающиеся под прямым, острым и ту­пым углами прямые линии (рис. - 58, а). Нужно построить сопряжения этих " пря­мых дугой заданного радиуса й.

Для всех трех случаев можно применять следующее построение.

Ь Находят точку О — центр сопряже­ния, который должен лежать на расстоя­нии 7? от сторон угла, т. е. в точке пересе­чения прямых, проходящих параллельно

а). 6) Рис. 57. Определение точки сопряжения

 

[p* / )

Я

6)

t

 

 

B)

Ptfc. 58. Построение сопряжения двух пересекающихся прямых

 

сторонам угла на, расстоянии Я от них (рис. 58, б).

Для проведения прямых, параллельных сторонам угла, из произвольных точек, взятых на прямых, раствором циркуля, рацнрм /?. делают засечки и к ним прово­дят касательные (рис. 58, б).

2. Находят точки сопряжений (рис. 58, а). Для этого из точки О опускают перпендикуляры на заданные прямые.

,3. - Из точки О, как из центра, описыва­ют дугу заданного радиуса /? между точ­ками сопряжений (рис. 58, а).

Сопряжение двух параллельных пря­мых. Заданы две параллельные прямые и на одной из них точка сопряжения М ' (рис. 59, а). Требуется построить со­пряжение.

Построение выполняют следующим об­разом:

)) находят центр сопряжения и радиус дуги (рис. 59, б). Для этого из точки М восставляют перпендикуляр до пересе­чения с прямой в точке М Отрезок ММ де­лит пополам (см. рис. 45);

2) из точки О — центра сопряжения ра­диусом ОМ = ОМ описывают дугу от точек сопряжения М и М (рис. 59, е).

Упражнение /4. Выполните чертеж шаблона, (рис. 60), применив правила построения сопря-

 

м^i

В)

Л?<Ь"

Рис. 6). Проведение касательной к окруж­ности

Л?о—

а)

Рис. 59. Построение сопряжения двух па­раллельных прямых

Рис. 60. Задание для упражнений.

 

жений. Линии построений не стирайте. Нанесите размеры и обозначения шероховатости поверх­ностей, имея в виду, что внутренние поверхности шаблона должны иметь шероховатости Да 0,80, а остальные Дз 12,5 Масштаб 1:1. Заполните основную надпись (материал — сталь 45 по ГОСТ 1050—88).

Проведение касательной к окружности. Даны окружность с центром О и точка 4. Требуется провести из точки /4 каса­тельную к окружности.

1. Точку /4 соединяют прямой с задан­ным центром О окружности.

Строят вспомогательную окружность диаметром, равным 04 (рис. 61, а). Что­бы найти центр О), делят отрезок СМ по­полам (см. рис. 45).

2. Точки М и М пересечения вспомога­тельной окружности с заданной — иско­мые точки касания. Точку /4 соединяют прямыми с точками М или Л/ (рис. 61,6). Прямая 4М будет перпендикулярна пря­мой ОМ, так как угол 4М0 опирается на диаметр.

Проведение прямой, касательной к двум окружностям. Даны две окружности ради­усов Д и #). Требуется построить прямую, касательную к ним.

Различают два случая касания: внеш­нее (рис. 62,6) и внутреннее (рис. 62, я).

При внешнем к а с а н и и построе­ние выполняют следующим образом:

1) из центра О проводят вспомогатель­ную окружность радиусом, равным разно­сти радиусов заданных окружностей, т. е.

R— #) (рис. 62, а). К этой окружности из центра О1 проводят касательную прямую 0]Л/. Построение касательной. показано на рис. 61;

2) радиус, проведенный из - точки О в точку М, продолжают до пересечения в точке М с заданной окружностью радиу­са 7?. Параллельно радиусу ОМ проводят радиус 0)Р меньшей окружности. Прямая, соединяющая точки сопряжений М и Р,— касательная к заданным окружностям (рис. 62, 6).

Рис. $2. Проведение касательной к двум ок­ружностям

 

При, внутреннем касании по­строение проводят аналогично, но вспомо­гательную окружность проводят радиусом, равным сумме радиусов Д + Д] (рис. 62, е). Затем из центра О) проводят касательную к: вспомогательной окружно­сти (см. рис. 6!). Точку М соединяют ра­диусом с центром О. Параллельно радиусу (М проводят радиус 0]Р меньшей окруж­ности. Искомая касательная проходит че­рез точки сопряжений М и Р.

Сопряжение дуги и прямой дугой задан­ного радиуса. Даны дуга окружности ра-

Рнс. 63. Построение сопряжения окружности и прямой

 

диуса Д и прямая. Требуется соединить их дугой радиуса Д).

!. Находят центр сопряжения (рис. 63, а), который должен находиться на расстоянии Д) от дуги и от прямой. Поэтому проводят вспомогательную пря­мую, параллельную заданной прямой, на расстояний, равном радиусу сопрягающей дуги Д) (рис. 63. а). Раствором циркуля, равным сумме заданных радиусов Д+Д), описывают из центра О дугу до пересече­ния с вспомогательной прямой. Получен­ная точка О) — центр сопряжения.

2. По общему правилу находят точки сопряжения (рис. 63, б): соединяют пря­мой центры сопрягаемых дуг О) и О и опускают из центра сопряжения О) перпендикуляр на заданную прямую.

3. Из центра сопряжения О] между точ­ками сопряжения А! и N проводят дугу, радиус которой Д) (рис. 63,6).

Сопряжение двух дуг дугой заданного радиуса. Даны две дуги, радиусы которых Д) и Д:. Требуется построить сопряжение дугой, радиус которой задан.

Различают три случая касания: внешнее (рис. 64, а, 6), внутреннее (рис. 64, а) и смешанное (см. рис. 66). Во всех случа­ях центры сопряжений должны быть рас­положены от заданных дуг на расстоянии радиуса дуги сопряжения.

Построение выполняют следующим об­разом:

Для внешнего касания:

)) из центров О] и Оз раствором цирку­ля, равным сумме радиусов заданной н со­прягающей дуг, проводят вспомогатель­ные дуги (рис.: 64, а); радиус дуги, прове­денной из: центра О], равен Д)+Дз; а радиус дуги, проведенной из центра О;, равен #!+йз.На пересечении вспомога­тельных дуг расположен центр сопряже­ния — точка Оз;

2) соединив прямыми точку О) с точкой Оз и точку Од с точкой Од, находят точки сопряжения М и (рис. 64,6);

3) из точки Оз раствором, циркуля, рав­ным Яз, между точками М и N описывают сопрягающую дугу.

Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов за­данной и сопрягающей дуг, т. е. #4—й) и #4—йж Точки сопряжения Р и К лежат на продолжении линий, соединяющих точ­ку О* с точками О] и О; (рис. 64, а).

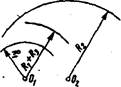
Для смешанного (внешнего и внутреннего) касания Л (]-й случай):

!) раствором циркуля, равным сумме радиусов и Яз. из точки О*, как из цент­ра, проводят дугу (рис. 65, а);

'2) раствором циркуля, равным разно­сти радиусов и Дз, из точки Од проводят

вторую дугу, пересекающуюся с первой вточкеОз (рис. 65,6);

3) из точки О) проводят прямую линию до точки Оз, из второго центра (точка Ой) проводят прямую через точку Оз до пе­ресечения ■ с дугой в, точке М (рис. 65, а).

Точка Оз является центром сопряжения, точки М и М — точками сопряжения:

4) поставив ножку циркуля в точку Оз, радиусом Дз проводят дугу между точками сопряжения М и М (рис. 65, а).

Для смешанного касания (2-й случай):

 

 

 

Рис. 65. Построение сопряжения двух дуг окружностей при сочетании внешнего и вну­треннего касании

'. дуг окружностей при смешанном ка­ саний

 

дано:

)) две сопрягаемые дуги окружностей радиусов Д] и Дэ (рис. 66);

2) расстояние между центрами О] и Оэ этих двух дуг;

3) радиус Дз сопрягающей дуги;

требуется:

]) определить положение центра Оз со­прягающей дуги;

2) найти на сопрягаемых дугах точки сопряжения;

3) провести дугу сопряжения.

Последовательность построения. Откла­дывают заданные расстояния между цен-

I трами О) и^лОй. Из центра О1 проводят

вспомогательную дугу радиусом, равным сумме радиусов сопрягаемой дуги радиуса j Д) и сопрягающей дуги радиуса Дз, а из

центра О: проводят вторую вспомогатель­ную дугу радиусом, равным разности ра­диусов Дз и Д:, до пересечения с первой вспомогательной дугой в точке Оз, которая | будет искомым Центром сопрягающей дуги

(рис. 66).

t I

Точки сопряжения находят по общему правилу, соединяя прямыми центры дуг Оз и 0<; Оз и Од. На пересечении этих прямых с дугами соответствующих окружностей находят точки М и М.

§ <4. ЛЕКАЛЬНЫЕ КРИВЫЕ

В технике встречаются детали, повер­хности которых ограничены плоскими кри­выми: эллипсом, эвольвентной окружно­стью, спиралью Архимеда и др. Такие кривые линии нельзя вычертить циркулем. Их строят по точкам, которые соединяют плавными линиями с помощью лекал. От­сюда название — лекальные к р и - в ы е.

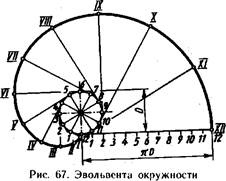
Эвольвента окруж но с т и при­ведена на рис. 67. Каждая точка прямой, если ее катить без скольжения по окруж­ности, описывает эвольвенту.

Рабочие поверхности зубьев большинст­ва зубчатых колес имеют эвольвентное зацепление (рис. 68).

Спираль Архимеда изображена на рис. 69. Это плоская кривая, которую описывает точка, равномерно движущаяся от центра О по вращающемуся радиусу.

По спирали Архимеда нарезают канав­ку, в которую входят выступы кулачков самоцентрирующего трехкулачкового пат­рона токарного станка (рис. 70). При вра­щении конической шестерни, на обратной стороне которой нарезана спиральная ка­навка, кулачки сжимаются.

Збольвенты

При выполнении этих (и других) ле­кальных кривых на чертеже можно для

облегчения работы воспользоваться спра­вочником.

Построение эллипса. Размеры эллипса определяются величиной его большой т4Я и малой СО осей (рис. 7)). Описывают две концентрические окружности. Диа­метр большей равен длине эллипса (боль­шой оси /!Я), диаметр меньшей — ширине эллипса (малой оси СС). Делят большую окружность на равные части, например на)2. Точки деления соединяют прямыми, проходящими через центр окружностей. Из точек пересечения прямых с окружно­стями проводят линии, параллельные осям эллипса, как показано на рисунке. При взаимном пересечении этих линий получа­ют точки, принадлежащие эллипсу, кото­рые, соединив предварительно от руки тон­кой плавной кривой, обводят с помощью лекала.

§!5. ПРАКТИЧЕСКОЕ

ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ

ПОСТРОЕНИЯ

Дано задание: выполнить чертеж клю­ча, показанного на рис. 72. Как это сде­лать?

Рис. 69. Спираль Архимеда

Рис. 70. Детали токарного пат­рона. имеющие форму спирали Архимеда

Рис. 7]. Построение эллипса

Прежде чем начинать чертить, проводят анализ графического состава. изображе­ния, чтобы установить, какие случаи гео­метрических построений необходимо при­менить. На рис. 72 показаны эти построе­ния.

Рис. 72. Анализ контура изображения ключа

 

Чтобы вычертить ключ, нужно провести взаимно перпендикулярные прямые, опи­сать окружности, построить шестиуголь­ники, соединив верхние и нижние их вер­шины прямыми, выполнить сопряжение дуг и прямых дугами заданного радиуса.

Какова последовательность этой рабо­ты?

Вначале проводят те линии, положение которых определено заданными размера­ми и не требует дополнительных построе­ний (рис. 73, а), т. е. проводят осевые и центровые линии, описывают по задан­ным размерам четыре окружности и соеди­няют концы вертикальных диаметров меньших окружностей прямыми линиями.

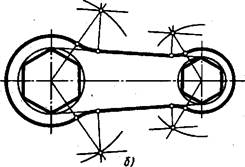Рис. 73. Последовательность выполнения гео­метрических построений при вычерчивании

Рис. 74. Задания для упражнений

Державка

/7/ммьййля М Rts

Дальнейшая работа по выполнению чер­тежа требует применения изложенных в § П и)2 геометрических построений. В данном случае нужно построить шестиу-

гольники и выполнить сопряжение дуг с прямыми (рис. 73,6). Это и будет вто­рой этап работы.

Контрольные вопросы

). Чему должен быть равен раствор циркуля при делении окружности на шесть равных час­тей?

2. Как определить построением центр и ради­ус данной дуги?

3. В каком месте должна находиться точка сопряжения дуги с дугой?

Уярюкжемме Я. По заданию ■ преподавателя выполните чертежи деталей, изображенных на рис. 74, о — е, применив правила ■ построения сопряжений. Линии построений не ■ стирайте. Нанесите габаритные размеры.

 

ГЛАВА II!

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

 

; 46, ОБЩИЕ СВЕДЕНИЯ

С помощью параллельного проецирова­ния, о котором говорилось в гл.!, получа­ют и один из видов наглядных изображе­ний предметов — аксонометриче­ские проекции.

Аксонометрические проекции получают­ся, если изображаемый предмет вместе с осями координат, к которым он отнесен, с помощью параллельных лучей проециру­ют на одну плоскость, называемую аксо­нометрической (см. рис. 77).

Слово *аксонометрия* — греческое. ' Оно состоит из двух слов: *ахсоп* — ось и *те(го* — измеряю. Перевод этого ело-

 

а) а)

Рис. 75 Сравнение чертежа в трех видах и аксонометрической проек­ции

ва означает измерение по осям, или изме­рение параллельно осям, так как размеры изображаемого предмета на чертеже от­кладывают только параллельно осям л, у, 2, называемым аксонометрическими осями координат.

Аксонометрические проекции применя­ют для пояснения чертежей машин, меха­низмов и их деталей. Это видно из сравне­ния чертежа, содержащего три вида па­раллелепипеда со срезами (рис. 75. а), с его аксонометрической проекцией (рис. 75,6). Без аксонометрической про-. екции представить форму изображенного предмета труднее.