Код высшей классификационной 7 глава

Построение на чертеже начинают с го­ризонтальной проекции (рис.)28, б). Из точки а, как из центра, радиусом, рав­ным аЬ, описывают дугу окружности М] до пересечения с прямой, проведенной из точки а параллельно оси л. Таким обра­зом, получают новую горизонтальную про­екцию точки В — точку 6]. Фронтальную проекцию 6] точки 6). получают, опустив из нее перпендикуляр на ось л. Соединив прямой точку а' с точкой А{ (проекцией точки В после поворота), получают нату­ральную длину отрезка АВ прямой.

На рис.)28, е показано, как определить натуральную длину ребра треугольной пи­рамиды.

йо/лурс/мляя длина

я) Рис.!28. Определение натуральной длины отрезка прямой способом вращения

Способ перемены плоскостей проекций. Способ перемены плоскостей проекций от-

/7/ММЦИЯ //С л/70/7//л/77ма -

С7

_{а (} ную плоскость

а о-'

 

 

А

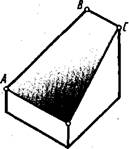
Рис. 129. Определение натуральной величины фигуры способом перемены плоскостей

Проекция на Заполнитель ную плоскость

проекций

 

личается от способа вращения тем, что проецируемый отрезок или грань остается неподвижной, а одна из плоскостей проек­ции ■ —■ Я2 или Л[ заменяется дополни­тельной плоскостью, на которую и проеци­руют изображаемый элемент. Заменим плоскость Л] новой плоскостью Л4. Пере­сечение НОВОЙ ПЛОСКОСТИ Я4 с плоско­стью Я2 (рис. 129, а) дает новую ось про­екций, которая обозначается Л). Новую систему плоскостей на чертеже будем обозначать Я4/Л2. Дополнительную плос­кость проекций Я4 располагают так, что­бы она была перпендикулярна фронталь­ной плоскости проекций Я2 (рис. 129, я) и параллельна отрезку или плоскости гра­ни, натуральную величину которой нужно определить. Тогда этот отрезок или грань спроецируется на дополнительную плос­кость без искажений. Новая ось проек­ции 2) будет параллельна фронтальной проекции наклонной грани (рис. 129,6).

Рассматривая наглядное изображение точки /1 на рис. 129, а, б, можно устано­вить, что при замене горизонтальной плос­кости Я плоскостью Я) расстояние новой проекции любой точки до оси проекций л< будет равно расстоянию горизонтальной проекции этой точки до прежней оси про­екций, т. е. расстояние точки 4 от плоско­сти ль остается неизменным. Этим и поль­зуются при построении проекций фигур на дополнительную плоскость, которую затем совмещают с плоскостью Чертежа.

На рис.!29, а точкЬ спроецирована сначала на плоскости Д2 и Л]. Получены ее, проекции а' и а. Взята дополнительная плоскость Л4, перпендикулярная плоско­сти Яд- Точка,4 проецировалась на допол­нительную плоскость. Для этого чз фрон­тальной проекции а' точки /4 проведена линия связи, перпендикулярная ли, перс сечение ее с осью Л! дало точку а,,. Затем от 1*очки а.,, отложено расстояние, рав­ное аа^л и получена искомая проекция а[ точки 4 на плоскость проекции 7л.

Наклонная линия Л1 на чертеже обозна - част ось проекций. Важно отметить, что фронтальная и новая проекции точки 4 на дополнительную плоскость лежат на од ном перпендикуляре к оси Л[.

На рис.)29. б представлено наглядное изображение четырехугольной призмы, верхняя грань которой наклонна. Чтобы определить натуральную величину этой наклонной грани, ее спроецировали на дополнительную плоскость. Построение проведано в следующем порядке. Вычерче­ны фронтальная и горизонтальная проек­ция призмы. На произвольном ра-стоянии проведена новая ось проекции Л1 парал­лельно фронтальной проекции изображае­мой грани. Из фронтальных проекций вер­шин наклонной грани —точек а'. 6'. с', - опущены перпендикуляры на ноную ось *[. На них отложены от новой оси Л; расстояния, равные расстояниям горизон­тальных проекций этих точек от оси л. Со­единив последовательно полученные точки й), й), С4 i прямыми, получаем натураль­ную величину грани.

Изображение детали на дополнительной плоскости называют в машиностроитель­ном черчении дополнительным видом (о дополнительных видах см. в § 47).

; 34. ПОСТРОЕНИЕ РАЗВЕРТОК ПОВЕРХНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ТЕЛ

Для изготовления кожухов машин, ог­раждений станков, вентиляционных ус­тройств. трубопроводов и других изделий необходимо из листового материала выре­зать их развертки.

Разверткой поверхности многогранника называют плоскую фигуру, полученную в результате последовательного совмеще­ния с плоскостью чертежа всех граней многогранника.

Построение разверток поверхности мно­гогранников состоит из определения нату­ральной величины граней и построения на плоскости в последовательном порядке всех граней. Размеры граней, если они спроецированы не в натуральную величи­ну. находят способами вращения или пе­ремены плоскостей проекций, приведенны­ми в предыдущем параграфе.

Рассмотрим построение разверток неко­торых простейших тел.

Рис.)30. Построение разверток поверхностей призмы и цилиндра

Развертка поверхности прямой призмы представляет собой плоскую фигуру, со­ставленную из боковых граней — прямо­угольников и двух равных между со<№л многоугольников оснований. Для примера взята правильная шестиугольная призма (рис.)30, а). Боковые грани призмы представляют собой равные между собой прямоугольники шириной а и высотой
а основания — правильные шестиугольни­ки со стороной, равной и. Так как разме­ры граней известны, построение развертки нетрудно выполнить. Для этого на гори­зонтальной прямой последовательно от­кладывают шесть отрезков, равных сторо­не основания а шестиугольника, т. е. 6а. Из полученных точек восставляют перпен­дикуляры длиной, равной высоте при­змы Я. Соединяя полученные отрезки, проводят вторую горизонтальную прямую. Полученный прямоугольник (//Хба) яв­ляется разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуру оснований — два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сги­ба — штрихпунктирной тонкой с двумя точками.

С помощью подобного построения ' мож- ' но вычертить развертки прямых призм с любой фигурой в основании. Разница будет лишь в количестве и ширине граней боковой поверхности.

Аналогично строится и развертка повер­хности цилиндра (рис.)30, б). Только ши­рина ее равняется лй (длине окружности основания).

Развертка поверхности правильной пи­рамиды представляет собой плоскую фигу­ру, составленную из боковых граней — равнобедренных или равносторонних треу­гольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида (рис.)3!,я). Решение задачи осложняется тем, что не­известна величина боковых граней пира- миды,,так как их ребра не параллельны ни одной из плоскостей проекций. Поэтому начинают построение с определения вели­чины ребра 54 способом вращения (см.' рис.)28, е). Определив длину на­клонного ребра 54, равную з'аТ, проводят из произвольной точки 5, как из центра, дугу окружности радиусом 5'а1. По этой дуге откладывают четыре отрезка, равных стороне основания пирамиды, которое на чертеже спроеиировалось в истинную ве­личину. Найденные точки соединяют пря­мыми с точкой $. Получив таким образом развертку боковой поверхности, пристраи­вают к основанию одного из треугольников квадрат, равный основанию пирамиды.

к

7 9-

Развертка поверхности прямого круго­вого конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. Ш, б).

Построение выполняют следующим об­разом. Проводят осевую линию и из точки, взятой на ней, как из центра, очерчивают радиусом Д;, равным обра­зующей конуса з'а', дугу окружности. Затем подсчитывают угол сектора по формуле а = '360° - /?/^Л, где й — радиус окружности основания конуса; А. — длина образующей боковой поверхности конуса. В примере а = 360° -15/38 * <з!42,2°.

Этот угол строят симметрично относи­тельно осевой линии с вершиной в точке 5. К полученному сектору пристраивают круг с центром на осевой линии и диа­метром, равным диаметру основания конуса.

$35. ВЗАИМНОЕ

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

ГЕОМЕТРИЧЕСКИХ ТЕЛ

о*

Рис. 131. Построение разверток поверхно­стей пирамиды и конуса

На чертежах деталей машин часто встречаются линии пересечения поверхно­стей. Поэтому необходимо изучить приемы построения этих линий.

Взаимное пересечение многогранников. На рис.!32, а приведены три изображе­ния двух пересекающихся призм: четырех­угольной и треугольной. Построение фронтальной проекции не закончено: про­екция линии пересечения на ней не показа­на. Требуется ее построить.

Рассматривая горизонтальную и про­фильную проекции, можно установить, что боковые грани вертикально расположен­ной призмы перпендикулярны горизон­тальной плоскости проекций, следователь­но, проекция линии пересечения на эту плоскость совпадает с проекциями боко­вых граней, т. е. с отрезками прямых. По той же причине профильная проекция ли­нии пересечения совпадает с профильной проекцией граней треугольной призмы. Никаких дополнительных линий на этих проекциях не будет (рис. 132, б). Следо­вательно, решение задачи сведется к по­строению фронтальной проекции линии пе­ресечения. Для этого нужно найти точки пересечения ребер первой призмы с граня­ми второй и ребер второй с гранями пер­вой.

Для облегчения рассуждений вначале определяют ребра каждой из призм, кото­рые. Ме пересекают граней другой. Эти ребра на рис. 132,6 не.помечены цифра­ми. Затем, рассматривая профильную и горизонтальную проекции, можно ви­деть, что ребра /—2 и Л—4 пересекают наклонные грани треугольной призмы. Места пересечения — точки встречи ребер /—2 и Л—4 с профильной проекцией треу­гольной призмы, т. е. а", 6", аК" видны на чертеже. Проекции точек, находящихся сзади, заключены в скобки. Горизонталь­ные проекции а, Ь. с, % точек Л, В, С, О лежат на горизонтальных проекциях ребер 7—2 и <!—4, которые сами изобра­жаются в виде точек. Фронтальные проек­ции —■ точки а', 6', с', d'— определяют с помощью линии связи. Далее устанавли­вают, что ребра 5—6, 7—<9 треугольной призмы пересекают грани четырехуголь­ной. Горизонтальные проекции этих то­чек — точки е, й — видны на черте­же. Фронтальные проекции точек Е,, С, Я находят, проводя линии связи на проек­ции соответствующих ребер.

Чтобы получить проекцию линии пересе­чения, нужно соединить полученные точки прямыми. Соединяют те точки, которые

-)?!? э I

Рис. 132. Построение линии пересечения двух призм -

' э

.??

\

лежат на одних и тех же гранях каждой призмы. Следовательно, нужно последова­тельно соединить точки а', А', ^А', <%', с', f, е'. Отрезки е'?' и^— линии пересе­чения на фронтальной проекции — неви­димы, так как закрыты наклонными граня­ми треугольной призмы. Поэтому их обво­дят штриховой линией.

Наглядное изображение пересекающих­ся призм дано на рис. 432.. а.

На рис. 133 показано построение линии пересечения четырехугольной усеченной пирамиды и четырехугольной призмы с ос­нованиями в виде ромбов. Построение вы­полнено аналогично приведенному на рис. 132. На фронтальной проекции линия пе­ресечения совпадает с проекцией боковых граней призмы, так как они перпендику­лярны фронтальной плоскости проекции. Верхнее и нижнее ребра призмы пересека­ются с передним и задним ребрами пира­миды в точках Д, <3, 4, проекции кото­рых V", 2", У, 4" находятся в точках пересечения проекции соответствующих ребер. Имея фронтальные и профильные проекции точек /. 2, 3, 4, находят гори­зонтальные их проекции с помощью линий связи, как показано стрелками на черте­же. Точки пересечения других двух ребер призмы с гранями пирамиды без дополни­тельного построения получить нельзя. Что­бы определить эти точки, призму и пира­миду пересекают горизонтальной секущей плоскостью Р, как показано на рис. 133. В результате пересечения плоско­сти Р с пирамидой образуется ромб, сто­роны которого будут параллельны сторо­нам оснований пирамиды. Его легко по­строить, перенеся точку а' на горизон­тальную плоскость проекций и проведя прямые, параллельные сторонам основа­ния. В результате пересечения плоско­стью Р призмы образуется прямоуголь­ник, равный размеру горизонтальной про­екции призмы. Точки 5, б, 7, & пересечения контуров ромба и прямоугольника и будут искомыми точками линии пересечения обо­их тел. Как получить профильные проек­ции Д", 6", 7", Й" этих точек,.показано на чертеже линиями связи со стрелками. В скобках проставлены проекции точек, находящихся сзади. Соединив прямыми проекции точек, лежащих на одних и тех же гранях пирамиды и призмы, т. е. точки /, 5, 2, 5, точки Л, <$, 4, 7, точки 7", У, 2" и точки 3", 7", 4", получают проекции линии пересечения. Подробнее об этом способе см. ниже.

L

Взаимное пересечение тел вращения. На рис. 134 показано построение линии пе­ресечения двух цилиндров разных диамет­ров. Оси цилиндров взаимно перпендику­лярны и пересекаются.

Рис.!33. Построение линии пересечения, четы­рехугольной призмы и усеченной пирамиды

 

На рис. 134, а изображена деталь (трой­ник, служащий для соединения труб, и его модель), представляющая собой два пе­ресекающихся цилиндра. Пересекаясь, ци­линдрические поверхности образуют про­странственную кривую линию. Горизон­тальная проекция линии пересечения совпадает с горизонтальной проекцией вертикально расположенного цилиндра, т. е. с окружностью (рис. 134,6). Про­фильная проекция линии пересечения со­впадает с окружностью, являющейся про­фильной проекцией горизонтально распо­ложенного цилиндра. Отмечают на гори­зонтальной и профильной проекциях ха­рактерные точки 7, 2, 3. По горизонталь­ной и профильной проекциям точек /, 2,.3 находят их фронтальные проекции 7', 2', Таким образом найдены проекции то­чек, определяющих линию перехода.

В ряде случаев такого количества точек недостаточно. Чтобы получить дополни­тельные точки, можно применить способ вспомогательных секущих плоскостей.

Способ вспомогательных секущих плос­костей. Этот способ заключается в том, что поверхности тел пересекают вспомога­тельной плоскостью, образующей фигуры сечений, контуры которых пересекаются. Точки, полученные в результате пересече­ния контуров сечений, находятся на линии пересечения.

В данном случае оба цилиндра пересе­кают вспомогательной секущей плоско­стью Р (рис. [34,а,8). При пересечении вертикально расположенного цилиндра образуется окружность, а горизонтально расположенного цилиндра — прямоуголь­ник.

Точки пересечения 4 и 5 окружности и прямоугольника принадлежат обоим ци­линдрам и, следовательно, находятся на линии пересечения обоих тел (рис. [34, а).

Отметив профильные, а затем горизон­тальные проекции точек 4 и 5, которые лежат на окружностях, находят с по­мощью линий связи их фронтальные про­екции, как это показано стрелками на рис. [34, а.

Полученные пять точек соединяют плав­ной кривой

При необходимости увеличить количест­во точек, определяющих линию пересече­ния, проводят еще несколько параллель­ных секущих плоскостей.

Если оба цилиндра имеют одинаковые диаметры, то одна из проекций их линий пересечения представляет собой пересека­ющиеся прямые (рис. 134, л, <3), а в про­странстве линии пересечения — эллипсы.

Линия пересечения шара и прямого кру­гового цилиндра, ось которого проходит через центр шара, показана на рис. [35. Как видно из чертежа, на одной проекции линия пересечения изображается окруж-, ностью, а на другой проецируется в пря­мую линию.

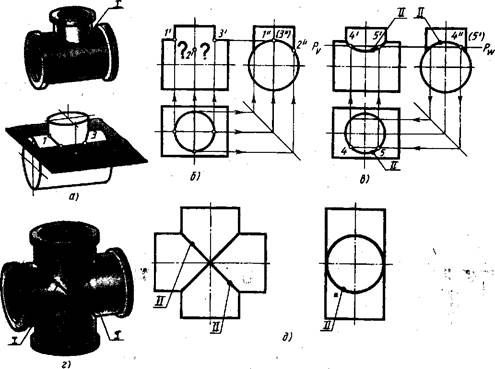Рис.!34. Построение линии пересечения цилиндров: линия пересечения; // — проекция линии пересечения

Проецирование тел ч: отверстиями. В технике встречается много деталей, име­ющих отверстия цилиндрической, прямоу­гольной, треугольной или смешанной фор­мы (рис. [36). При пересечении отверстий с поверхностями деталей образуются ли­нии пересечения, которые необходимо по­строить на чертеже. Задача эта решается
в общем врде темн же методами, что и по­строение линий пересечения геометриче­ских тел. В каждом случае отверстие мож­но рассматривать как тело, проходящее через данную деталь.

На рис. 137, а показан цилиндр, имею­щий отверстие цилиндрической формы. Оси цилиндра и отверстия пересекаются под прямым углом. Линия пересечения изображается кривой. Построение такой линии было показано на рис. 134. На рис. 137, а показано, как получить характерные точки данной кривой.

Рис. 135. Построение линии пересечения шара и ыилиндра: /- линия пресечения; Д- проекций линии пересечения

Линия пересечения цилиндра с отверг стием прямоугольной формы в случае пе­ресечения их осей под прямым углом пока­зана на рис. 137, б. Для ее построения на горизонтальной проекции выбраны харак­терные точки 2, Л, 4, 5, 6. Профильные их проекции 2", У, 4", 5", 6" лежат на окружности, являющейся проекцией ци­линдра. Фронтальные проекции /',2', У. 4', 5', 6' находят по полученным гори­зонтальным и профильным. Соединив точ­ки 2/,' Л\ 4', 5', 6' прямыми, получают

Рис. [36. Детали с отверстиями

 

проекцию линии пересечения в виде пря­моугольной впадины. Проекция линии пе­ресечения с другой стороны отверстия имеет ту же форму.

49.

На рис. 137, а показана линия ' пересече­ния цилиндра с отверстием, являющимся комбинацией первых двух. Отверстие об­разовано четырехугольной призмой и дву­мя полуцилиндрами. Т.акую форму имеет шпоночная канавка.

Выполните задание

Упражнение (рис. 138).

По двум данным проекциям начертите третью. Постройте недостающие проекции то­чек <4 и Д, заданных своими видимыми проекци­ями а и М. Выполните аксонометрическое изо­бражение, проставьте на нем размеры и нанеси­те точки /4 и В.

Ответьте на вопросы (к рис. 138)

1. Какие виды представлены на чертеже?

2. Чему равны габаритные размеры детали?

3. Каковы размеры прямоугольного паза на детали?

4. Какова шероховатость поверхности, изо­браженной штриховой линией на главном виде?

5. Нужно ли обрабатывать ' основания детали и ее боковые грани?

6. Нужно ли обрабатывать верхнюю наклон­ную плоскость детали?

Упражнение ДА Выполните задание (рис. [39).

По заданным проекциям детали начертите третью (М 1:2). Постройте две недостающие проекции точки И, лежащей на видимой повер­хности детали и заданной своей фронтальной проекцией а'.

Ответьте на вопросы (к рис [39)

[. Какими видами задан чертеж?

2. Какова исходная форма детали?

3. Что обозначают штриховые линии на фрон­тальной проекции?

4. Что обозначают две вертикальные штрихо­вые линии на профильной проекции? две гори­зонтальные?

5. Чем вызвано появление на фронтальной проекции двух кривых линий?

6 Можно ли без дополнительных построений обозначить на виде слева фронтальную проек­цию точки В?

7. Каковы габаритные размеры детали?

8. Как определить, где сверлить отверстие диаметром 40 мм?

9. Допустимо ли обточить деталь под размер 49,98 мм?

[0. Допустимо ли обтсмить деталь под размер

 

 

Н9,8 мм? Если нет, то будет ли такой брак исправимым?

1). Допустимо ли паз шириной 60 мм обрабо­тать под размер 60-о.)? Если нет, то можно ли такой брак исправить?

)2. Нужно ли наносить размер между линия­ми, - обозначенными цифрой / на полке? В ре­зультате чего образовались эти линии?

)3. Какова должна быть шероховатость большей части поверхностей детали?

!4. Какова шероховатость двух параллель­ных плоскостей в каждом из пазов?

Упражнение 5/. По наглядным изображени­ям деталей, представленным на рис.!40, а —

выполните их чертежи в системе прямоуголь­ных проекций.

Контрольные вопросы

). Как располагаются виды на комплексном чертеже?

2. Как обозначают на чертежах дополнитель­ные виды?

3. В виде каких фигур проецируются гео­метрические тела: цилиндр, шар, куб, призма?

4. Какова последовательность построения чертежа детали?

5. Как строится вспомогательная прямая комплексного чертежа?

6. Чем отличается способ вращения от спосо­ба перемены плоскостей проекций? Для чего эти способы применяются?

7. В чем состоит способ вспомогательных секущих плоскостей? Когда его применяют?

 

ГЛАВ А V

СЕЧЕНИЯ И РАЗРЕЗЫ

; 36. СЕЧЕНИЯ

 

. В гл.! указывалось, что. изображения на чертежах в зависимости от их содержа­ния делятся на виды, разрезы и сечения. С помощью видов' форма некоторых дета-, лей не выявляется с достаточной полнотой и удобочитаемостью. Например, форма та­кого распространенного несложного изде­лия, как гаечный ключ, остается невы­ясненной с помощью двух видов, данных на рис. 141, а. По этим видам нельзя уста­новить. какова поперечная форма ручки, которая может быть и прямоугольной, и овальной, и закругленной на углах. То же самое можно сказать и о плоскогубцах (рис.)4], б), поперечная форма губки ко­торых не выявится и третьим видом, так как она изогнута и изменяется по длине. Третий вид, если его выполнить, окажется пересеченным множеством линий, малопо­нятным и не разъяснит форму детали.

Чтобы показать поперечную форму де­талей, пользуются изображениями, назы­ваемыми сечениями (рис.!42). Для того чтобы получить сечение, деталь мысленно

 

с; я;

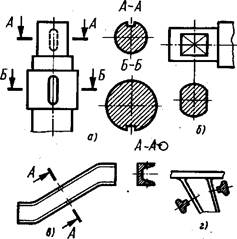
Рис. 14!. Детали, для выявления формы которых требуются сечения

Секущие мосшти Рис.)42. Образование сечений

 

рассекают воображаемой секущей плоско­стью в том месте, где нужно выявить ее форму.

Фигура, полученная в результате рассе­чения детали секущей плоскостью, изобра­жается на чертеже.

Следовательно, сечением называется изображение фигуры, получающейся при мысленном рассечении предмета плоско­стью (или несколькими плоскостями). На сечении показывается только то, что полу­чается непосредственно в секущей плоско­сти.

бразив на чертеже образовавшиеся плос­кие фигуры (т. е. только то, что находится в секущей плоскости), получают сечения. Для ясности чертежа сечения выделяют штриховкой. Наклонные параллельные прямые линии

Ш//А
	\

а)

	—1		-------

6)

Рис. [43. Расположение сечений

Построение сечений. На рис.)42, а изо - бражен ступенчатый вал, имеющий две лыски (плоские срезы с двух сторон) и шпоночную канавку (прямоугольное уг­лубление с полукруглыми концами, пред­назначенное для шпонки). По чертежу этого вала (рис. 142, е) в. случае отсутст­вия сечений было бы трудно определить форму и глубину шпоночной канавки, ко­личество лысок (одна или две) и их форму (плоская или нет). Вид слева поможет ответить на эти вопросы, но будет неяс­ным, так как часть линий на нем совпадет, а шпоночная канавка будет показана штриховой линией, что вызовет затрудне­ния в простановке ее размеров, которые не рекомендуется наносить у невидимого кон­тура. Чтобы сделать чертеж более ясным, строят сечения. Для этого мысленно рас­секают вал двумя секущими плоскостями /4 и Б, перпендикулярными оси вала (рис. 142, б).Плоскость /4 проходит попе­рек лыски и показывает поперечную фор­му детали в этом месте. Плоскость Б, рассекающая вал поперек шпоночной ка­навки, выявляет ее глубину и форму. Изо­— 87 —

штриховки проводят под углом 45° к лини­ям рамки чертежа (рис. [42, [43), а если они совпадают по направлению с линиями контура или осевыми линиями, то под уг­лом 30 или 60° (см. рис. [42).

Расположение сечений. ' В зависимости от расположения сечения подразделяются на вынесенные и наложенные.

Вынесенными сечениями на­зываются такие, которые располагаются - вне контуров изображений, приведенных на чертеже (см. рис.)4[,б).

Наложенными сечениями на­зываются такие, которые располагаются непосредственно на видах чертежа (см. рис. [4[, а).

Вьшесенным сечениям следует отдавать ' предпочтение перед наложенными, так как последние затемняют чертеж и неудобны для нанесения размеров.

Контур вынесенного сечения обводится сплошной основной линией такой же тол­щины (^Л), как видимый контур изображе­ния.

Контур наложенного сечения обводят сплошной тонкой линией (от $/3 до ж/2). Если при этом сечение закрывает контур-' ные линии вида, то они не прерываются в месте расположения наложенного сече­ния.. Наложенное сечение располагают в том месте, где проходила секущая плос­кость, и непосредственно на самом виде, к которому оно относится (рис. [43, а), т. е. как бы накладывают на изображение, откуда и произошло название жналожен- ное сечение*.

Вынесенное сечение можно располагать на любом месте поля чертежа. Оно может быть помещено непосредственно на про­должении линии сечения (рис. [43, б) или в стороне от этой линии. Вынесенное сече­ние может быть размещено на месте, пред­назначенном для одного из видов (рис. [43, а)Л а также в разрыве между частями одного и того же вида (рис. [43, а).

Обозначение сечений. Положение секу - щей плоскости указывают на чертеже ли­нией сечения.

Ось симметрии наложенного или вы­несенного сечения указывают штрих- пунктирной тонкой линией без обозначения буквами и стрелками и линию сечения не проводят (рис. [43, а, б; [44,6). Во всех остальных случаях для линии сече-