Код высшей классификационной 5 глава

метрии (рис. 98, (?) можно нарисовать, если на оси, расположенной под уг­лом 30°, отложить четыре равных отрезка (4а), а на вертикальной оси — примерно 3,5 таких же отрезка. Это позволит наме­тить вершины шестиугольника, сторона которого будет равна 2а. Следовательно, отрезок а, с помощью которого проведено построение, берется равным половине сто­роны изображаемого шестиугольника. Чтобы построить эллипс (рис. 98, е, эк), нужно длину большой оси разделить на пять примерно равных отрезков. Тогда малая ось составит три таких отрезка.

Если технический рисунок выполняется на бумаге, разлинованной в клетку, то аксонометрические оси удобно строить по соотношению клеток, как показано на рис. 99.

На рис. 99, а проведены оси для фрон­тальной диметрической проекции. Угол 45° получается в результате проведения диагонали квадрата.

На рис. 99, б приведен способ построе­ния осей изометрической проекции. Со­отношение катетов прямоугольного тре­угольника 7:4 дает угол, близкий к 30°.

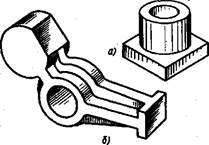
Технические рисунки становятся более наглядными, если на них нанести штри­ховку. Выполняя штриховку, предполага­ют, что свет падает на предмет слева и сверху. Освещенные поверхности остав­ляют светлыми, а теневые покрывают бо­лее частой штриховкой (рис. Юо, а). Можно для выявления рельефности форм предмета накладывать штриховку не по всей поверхности детали, а только в мес­тах, подчеркивающих образование цилин-

 

Рис. ЮО. Способы выявления объема на техническом рисуике

дрических и других элементов (рис.)оо,б).

Для выявления внутренних очертаний предметов при построении аксонометриче [ - ских проекций и технических рисунков л применяют вырезы (рис. Ю!.а). При этом рассеченное место заштриховывают так, как показано на рис. Ю),б. Вырезы выполняют плоскостями, параллельными плоскостям проекций.

} Упражнение 29. Проведите от руки прямые

. линии под углами 30. 45 и 60° к горизонтали.

' Упражнение 30. Нарисуйте чо три эллипса,

изображающих в изометрии окружности, плос­кости которых расположены соответственно перпендикулярно осям х, у,?.

Упражнение 3/. Выполните технический рису­нок куба со стороной, равной 40 мм.

Упражнение 32. Выполните технический рису­нок детали, которую вам укажет преподаватель на рис. 86 или 94.

 

Для изометрической Для фронтальной проекции диметрической проекции

ю

Ко

Рис. НМ. Вырезы в аксонометрических проек­циях

нтрольные вопросы

1. Под какими углами располагаются оси фронтальной диметрической проекции? Чо ка­кой оси сокращаются размеры?

2. Какова последовательность построения фронтальной диметрической проекции?

3. Как располагаются оси изометрической проекции? Производится ли сокращение разме­ров но ее осям?

4. Как строят овалы, заменяющие эллипсы в изометрии?

5. Что называют техническим рисучком?

ГЛАВА, IV

ЧЕРТЕЖИ В СИСТЕМЕ ПРЯМОУГОЛЬНЫХ ПРОЕКЦИЙ

 

§ 24. ПРЯМОУГОЛЬНОЕ

ПРОЕЦИРОВАНИЕ

В гл.! указывалось, что когда проеци­рующие лучи составляют с плоскостью проекций прямой угол, то такие парал­лельные проекции называются прямоу - гольными [4].

Чертежи в системе прямоугольных про­екций дают полные сведения о предмете, так как он изображается с нескольких сторон. Чертежи, выполняемые методом прямоугольного проецирования, легче строить, чем аксонометрические изобра­жения. Прямоугольные проекции дают, как правило, ясное представление о форме и размерах предмета. Поэтому в производ­ственной практике пользуются чертежами, содержащими два, три или более изобра­жений, полученными в результате прямо­угольного проецирования.

Предмет, имеющий плоские поверхно­сти, ограничивается вершинами, ребрами, гранями (рис. Ю2).

Следовательно, для того чтобы научить­ся изображать на чертежах различные предметы, необходимо знать, как в прямо­угольных проекциях изображаются вер­шины - (точки), ребра (Ьтрезки прямых), грани (отсеки плоскости).

Чтобы понять, как получается прямо­угольная проекция предмета, поместим лист плотной бумаги параллельно стене, против окна. Эту стену примем за плос­кость проекций. Параллельные лучи све­та из окна падают на стену и предмет перпендикулярно.

Лучи показаны на рис. ]03 тонкими линиями со стрелками. От листа бумаги на стене образуется тень, которую можно принять за его проекцию (рис. ЮЗ, а). ' Нетрудно заметить, что проекция в этом случае по контуру и размерам соответ­ствует объекту проецирования—листу бумаги. Если лист поворачивать вокруг его стороны /№, то можно заметить, как тень будет все более сокращаться по ши­рине (линии а'М и с'%' на рис. ЮЗ. б). Когда лист бумаги займет положение, пер­пендикулярное стене, его изображение превратится в линию (рис. ЮЗ, а).

При этом можно заметить, что высота предмета все время изображалась в нату­ральную величину, т. е. не изменялась длина отрезков а'бГ и 6'с'.

Из подобного опыта можно сделать сле­дующие важные выводы. При прямоуголь­ном проецировании:

плоская фигура, параллельная плоско­сти проекций, изображается на ней в нату­ральную величину (рис.)03, а);

плоская фигура, наклонная к плоскости проекций, изображается на ней с искаже­нием размеров (рис. ЮЗ, б);

плоская фигура, перпендикулярная плоскости проекции, изображается на ней в виде отрезка прямой (рис. ЮЗ, а).

Эти выводы относятся к изображению плоских фигур (граней предметов).

А как в прямоугольных проекциях изо­бражаются ребра предметов, т. е. отрезки?

Отрезок прямой, параллельной плоско­сти проекций, изображается на ней в нату­ральную величину (см. отрезки 40 и ВС

Вершины

Грани

Рис. НИ. Предмет как совокупность граней, ребер, вершин

 

на рис. ЮЗ, а — ей отрезки /1В и СО на рис. ЮЗ. а);

отрезок примой, наклонной к плоскости проекций, изображается на ней искажен­ным (см!, отрезки /!В и СО на рис. ЮЗ, б);

отрезок прямой, перпендикулярный плоскости проекций, изображается на ней точкой (см. отрезки,4В и СО, расположен­ные перпендикулярно плоскости проекций, на рис. ЮЗ, а);

чтобы получить проекцию точки, необхо­димо опустить из нее на плоскость проек­ции перпендикуляр, т. е. точки а', М, с', являются проекциями точек И, В, С, О. При проецировании точки в пространст­ве обозначают заглавными (прописными) латинскими буквами,4, В, С, О и т. д., а проекции точек — соответствующими малыми (строчными) буквами а, &, с, <% и т. д.

Из двух совпадающих на чертеже точек (рис. ЮЗ, я) одна является изображением видимой вершины, другая невидимой (за­крытой). Обозначение проекций невиди­мых вершин условно заключают в скобки.

§25. ПЛОСКОСТИ ПРОЕКЦИЙ

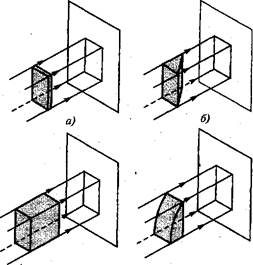
По изображению предмета л на одной плоскости проекций во многих случаях нельзя судить о его форме и размерах. Предметы,показанные на рис.)04,— пря­моугольная пластинка, треугольная приз­ма, прямоугольный параллелепипед и па­раллелепипед с частью цилиндра,— дают в этом случае одинаковые проекции в виде прямоугольника.

По одной проекции можно судить лишь о двух измерениях предмета.

Но и две проекции предмета часто недо­статочно полно отображают его форму. Так, например, две проекции прямоуголь­ного параллелепипеда (рис. Ю4, а. б) не­однозначно отображают его форму. Такие две проекции могут иметь и треугольная призма (рис. Ю4. б), и призма с закругле­нием (рис. Ю4, <?), и т. д.

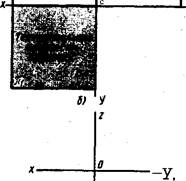
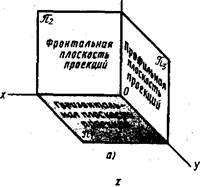
Чтобы получить полное представление о форме и размерах предмета, его нужнб спроецировать на две, три или более плос­костей. Для простоты проецирования эти плоскости располагают взаимно перпенди­кулярно. Таким образом, три плоскости образуют прямой трехгранный угол (рис. Ю5, а). Каждой плоскости дано на­звание и обозначение (рис.!05, а, б).

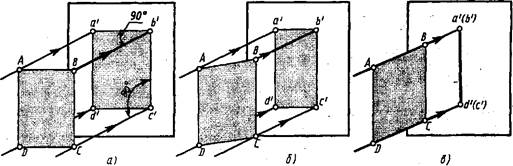Рис. 103. Проецирование плоской фигуры

— 5 7 г -

Вертикальная плоскость, расположен­ная прямо перед нами, называется фрон-

в) г) Рис.)04. Проекции разных нм форме предме­тов на одну плоскость

 

*' у

Рис.!05. Плоскости проекций

z

_____________ I____________ лг Tt3

Фронтальная Профильная /МЙГЯЙГЯМ /ММ7МСЯМ проекции проекций

тальной плоскостью проекций. Она обоз­начается латинской буквой Л2- Под пря­мым углом к ней горизонтально распола­гается плоскость проекций, называемая горизонтальной плоскостью. Она обозна­чается латинской буквой Л]. Перпендику­лярно этим, плоскостям располагается еще одна вертикальная плоскость, обозначен­ная буквой Лз называемая профильной плоскостью проекций. Попарное пересече­ние плоскостей трехгранного угла образу­ет прямые линии — оси проекций, исходя­щие из точки О. Пересечение фронтальной и горизонтальной плоскостей проекций об­разует ось д, фронтальной и профиль­ной — ось 2!. профильной и горизочталь- ной—ось у (рис.!05, б).

На рис. 105. а изображен трехгранный угол. Его грани взаимно перпендикулярны и не лежат в одной плоскости. Однако чертеж выполняется на плоскости. Для того чтобы изображения, полученные на сторонах трехгранного угла, оказались в одной плоскости, две грани этого угла развертывают до совмещения их с третьей гранью, т. е. до такого положения, когда все три плоскости трехгранного угла ока­жутся в одной плоскости. Для этого гори­зонтальную плоскость поворачивают во круг оси % вниз на 90°. Профильную плос­кость поворачивают вокруг оси 2 на 90° вправо, как показано стрелками. Тогда обе эти плоскости совмещаются с непо­движной фронтальной. При этом горизон­тальная плоскость располагается под фронтальной, а профильная — справа от фронтальной (рис.)05, б).

Ось у как бы распадается на две: - у и у).

Линии, ограничивающие плоскости про­екций квадратами, взяты условно и значе­ния не имеют, поэтому их обычно не про водят. Тогда плоскости проекций изобра­зятся, как показано на рис.)05, а.

§ 26. КОМПЛЕКСНЫЙ

ЧЕРТЕЖ ПРЕДМЕТА

Изучив, как строят проекции точек, от резков прямых и плоских фигур, т. е. эле­ментов, которые ограничивают различные предметы (изделия или их составные час­ти), можно перейти к рассмотрению спосо­бов получения прямоугольных изображе­ний самих предметов.

На рис.)06,а представлен прямой трехгранный угол. Перед его плоскостями помещен изображаемый предмет — упор. Он расположен так, чтобы возможно боль­шее число его граней было параллельно или перпендикулярно плоскостям проек- * ций. Это значительно облегчает процесс проецирования.

Чтобы получить прямоугольные проек­ции изображаемого предмета, необходимо провести проецирующие лучи перпендику­лярно плоскостям проекций.

Спроецируем упор на фронтальную плоскость проекций Л2- Точки пересечения проецирующих лучей с этой плоскостью дадут проекции вершин упора. Соединив

ч) а' Ь'

оа"

О

У

6)

,а(Ь)

Рис. 106. Образование комплексного чертежа

Фронтальная

проекция

Горизонтальная/ проекция

Яг	а'	Яз
	/					,4*
				Ь'
					О
а(Ь) Jit

 

б)

 

соответствующим образом эти точки, по­лучим фронтальную проекцию, или вид спереди. Вид спереди называют также главнымвидом.

Построим проекцию упора на горизон­тальной плоскости проекции п, — вид сверху. Для этого опустим на горизонталь­ную плоскость перпендикуляры, проходя­щие через вершины упора, и полученные точки их пересечения с плоскостью соеди­ним отрезками прямых.

Проведя проецирующие лучи на про­фильную плоскость проекций лГ и вьшол-. нив построения, аналогичные предыду­щим. получим профильную проекцию изо­бражаемого предмета — вид слева.

Сравнивая наглядное изображение упо­ра с его проекциями (рис. 106, а) и вспо­миная изученное, можно установить сле­дующее.

Во-первых, проекции упора на каждой из плоскостей проекций Я2, Дь Пз представ- _: ляют собой изображения не только одной стороны детали, но всего предмета, всех его вершин, ребер и граней, если на гори­зонтальной и профильной проекциях штриховыми линиями показать невидимый сверху и слева контур детали. На фрон­тальной плоскости проекций видна лишь передняя грань упора. Это происходит по­тому, что боковые грани, перпендикуляр­ные плоскости проекций, изобразились на
ней в виде отрезков прямых. Грани, па­раллельные ' соответствующим плоскостям проекций, ' изображаются без искажения размеров.

Во-вторых, ребра, перпендикулярные плоскости проекций, изобразились на ней в виде точек (например, ребр^А на горизонтальной плоскости проекций), а ребра, параллельные плоскости нроек ций, изобразились на ней в натуральную величину (например, ребро-4Ана фрон­тальной и профильной плоскостях проек­ций).

В третьих, наклонная грань упора ни на одной плоскости проекций не изобрази­лась в натуральную величину, хотя размер одной стороны этой грани можно измерить по проекции ее ребра, параллельного фронтальной плоскости проекций, а раз мер другой — по проекции ребра, парал­лельного горизонтальной й профильной плоскостям проекций, на одной из них.

Развернем плоскости проекций так, как это было показано на рис.)05. чтобы сов­местить их в плоскости чертежа (рис. Ю6. б). Фронтальная плоскость П2 при этом остается неподвижной, гори­зонтальная Л] поворачивается вокруг оси х вниз на 90°, профильная лз повора­чивается вокруг оси 2 на 90° вправо. Тог - да виды расположатся так: вид сверху — под главным видом, а вид слева справа от главного вида и на уровне его.

Фронтальные и горизонтальные проек­ции одноименных точек находятся при этом на одних перпендикулярах к оси % (например, фронтальная а' и гори­зонтальная а проекции точки /4[5]. а их фронтальные и профильные проекции рас­полагаются на одних перпендикулярах к оси 2 (например, фронтальная а' и про­фильная а" проекции точки <4). Эти пер­пендикуляры называют линиями с в я з и. Таким образом, все три проекции упора оказываются связанными между со­бой. Положение любых двух проекций оп ределяет положение третьей.

На чертежах не проводят рамки, огра­ничивающие плоскости проекций, и линии связи (см. рис.)05, я). Удалив их, мы получим чертеж, представленный на рис. Ю6, а.

Иногда изображения предмета на сов­мещенных плоскостях проекций называ­ют комплексным чертежом.

Так строят чертежи в системе прямо угольных проекций. Однако нас интересу - ет не только построение чертежей, но и чтение их, т. е. процесс представления пространственной формы предмета по его плоским изображениям.

Л - А Рис.)07. Задание к упражнению

Для того чтобы прочитать чертеж, нуж­но представить себе, в результате чего получилось на нем то или иное изображе­ние. подумать, какое тело могло дать рас­сматриваемую проекцию. При этом нельзя рассматривать проекции изолированно од­ну от другой. Необходимо мысленно

объединить в единое целое представлении о всех проекциях, данных на чертеже.

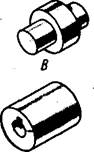
Упражнение 33. По рисункам предметов най­дите их чертежи я прямоугольных проекциях (рис. Ю7). Запишите в рабочей тетради, како­му рисунку, обозначенному буквой, соответству­ет чертеж, обозначенный цифрой.

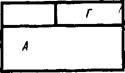
Упряжмемме34. Определите и запишите в ра - бочей тетради, какой поверхности детали, обоз­наченной буквой на наглядном изображении, соответствуют ребра и грани, обозначенные цифрами на чертеже (рис.)08).

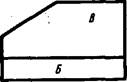
Упражнение 35. Найдите на каждой из про - екций и запишите в рабочей тетради, какие поверхности, обозначенные буквами, перисиди кулярны фронтальной или горизонтальной плос­кости проекций (рис.)09).

Пример записи:

поверхность N перпендикулярна фронтальной и горизонтальной плоскостям проекций;

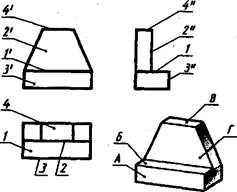Рис.)08. Задание к упражнению

поверхность /И перпендикулярна только фронтальной плоскости.

Упражнение 36. Перечертите рис. ПО и обоз- ■ начьте на всех проекциях плоскости, выделенные цифрами на наглядном изображении.

Контрольные вопросы

 

]. Как направлены проецирующие лучи при прямоугольном проецировании?

2. Что называется комплексным чертежом?

3. Как называются и как располагаются плоскости проекций?

4. Как располагаются три вида (проекции) на чертеже?

5. При каком условии ребро предмета проеци­руется в точку и при каком условии — в нату­ральную величину?

Рис.)09. Задание к упражнению

6. При каком условии грань предмета проеци­руется в линию и когда — в натуральную.вели чину?

 

§ 27. ПРОЕКЦИИ

ГЕОМЕТРИИ ЕСКИХ ТЕЛ

Формы деталей, встречающихся в тех­нике, представляют собой сочетание раз­личных геометрических тел или их частей.

Для выполнения и чтения чертежей де­талей нужно знать, как изображаются геометрические тела.

ГТ—г

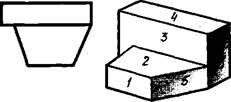Рис. НО. Задание к упражнению

Построение проекций прямого цилинд­ра с вертикальной осью (рис.)П,а) начинают с изображения основания ци­линдра, представляющего собой круг. По­скольку круг расположен параллельно плоскости проекций Я) и, следовательно,

изображается на ней без искажений, его горизонтальная проекция - круг, а фрон­тальная и профильная — горизонтальные отрезки прямых, равные диаметру круга. Фронтальная и профильная проекции ци­линдра очерчиваются отрезками прямых, представляющими проекции его основания и крайних образующих. На всех проекци­ях проводят оси симметрии. Размеры ци­линдра определяются диаметром его осно­вания и высотой.

Фронтальная и профильные проекции цилиндра одинаковы, поэтому в данном случае профильная проекция лишняя. На рис. ] 1) чертежи всех геометрических тел выполнены в трех проекциях лишь с той целью, чтобы показать, какие проекции эти тела имеют.

Одно изображение конуса вращения (рис. И), б) сходно с изображением цилиндра. Так, на горизонтальной про­екции конус изображен кругом. На нем наносят центровые линии. Диаметр круга равеА диаметру основания конуса. Два других изображения конуса — равнобед­ренные треугольники. На этих проекциях также наносят оси симметрии. Для ко­нуса указывают диаметр его основания и высоту.

На рис. П1,е представлены чертеж и наглядное изображение шара. Все про екции шара — окружности. Диаметр их равен диаметру шара. На каждом изобра­жении проводят центровые линии.

Так же как и шар, куб имеет три одина­ковые проекции (рис. [)),<?). Все грани его — квадраты. Размеры куба опреде­ляют три измерения: длину, ширину и высоту, равные между собой.

Построение изображений правильной треугольной призмы (рис. п).а) следует начинать с основания — равностороннего треугольника. На фронтальной плоскости проекций задняя грань призмы изобража­ется в натуральную величину, две перед­ние — с искажением ширины. На про­фильной проекции ширина прямоугольни­ка равна высоте фигуры основания призмы. На горизонтальной и фронталь­ной проекциях проводят осевые линии, на профильной проекции ось симметрии от­сутствует. Для правильной треугольной призмы указывают ее высоту, длину сторо­ны основания и угол.

Построение прямоугольных проекций правильной шестиугольной призмы (рис. И!, г) также начинают с вычерчи­вания вида сверху, который представляет собой правильный шестиугольник. На главном виде средняя грань изображает­ся в натуральную величину, а ширииа боковых граней искажена. На профильной проекции грани изображаются искажен­ными по ширине. Размеры правильной шестиугольной призмы определяют ее вы­сотой и шириной, равной удвоенной длине стороны основания.

На рис. Ш.эк приведены три проекции и наглядное изображение правильной че­тырехугольной пирамиды. Основание ее, параллельное горизонтальной плоскости проекций проецируется на нее в натураль­ную величину, т. е. изображается квадра­том. Боковые ребра, идущие из вершин основания к вершине пирамиды, изобра­жаются диагоналями. Фронтальная и про­фильная проекции представляют собой равнобедренные треугольники, высота коА торых равна высоте пирамиды. На всех проекциях должны быть. нанесены оси симметрии. Для правильной четырехуголь­ной пирамиды указывают длины двух сто­рон основания и высоту.

Аналогичны изображения правильной шестиугольной пирамиды (рис.)Н,.э). Горизонтальной проекцией ее является правильный шестиугольник с диагоналя­ми, изображающими боковые ребра пира­миды. На фронтальной проекции видны три грани, а на профильной — две. На всех проекциях проводят оси симметрии. Размеры правильной шестиугольной пира­миды определяются ее высотой й шириной, равной удвоенной длине стороны основа­ния.

Упражнение 37. [. Рассмотрите • чертежи, представленные на рис. И2. а — о. и ответьте на следующие вопросы применительно к каждо­му чертежу: *

)) Какие виды (проекции) даны на чертеже?

2) Из каких геометрических тел состоит де таль?

3) Каковы размеры каждого геометрического тела?

4) Какова шероховатость поиерхностен де­тали?

2. По указанию преподаватели выполните чер­теж и технический рисунок одного-двух геомет­рических тел. которые образуют форму детали.

1 -с0	| z ><\<Ри	' У / " -ч.	•Z У >KJ ——	А\А | 1	Z
Ф ф £	>		iry б)	*а» <51 фу	<1 Z / уЛЧ. Я	г)
trrJ \1у у Л -	Z	Z ЧУ Я	Ц--И 1-- Л.< Л Ж Л Л	lift. X ^ „
АЛ! iik j л ><а ------------ j л / _ ь _ ^	Z J хГ Гх.	At	А-А, Jв 1 1 $ ж J	л

 

Рис. Ш. Проекции геометрических тел

Рнс,[Л2 Чертежи для чтении (к упражнению)

см «i

)

л

6)

M l

ф

5хЬ5°

_ЗУ „

 

УярааммяисЗА Выполните комплексный чер­теж детали по приведенному ниже ее описанию и нанесите размеры.

Верхняя часть детали имеет форму цилинд­ра диаметром 35 мм. Вдоль оси просверлено глухое отверстие диаметра 20 мм и длиной 30 мм. Другой конец детали представляет собой иризму. Размеры основания призмы 24X24 мм. высота ее 30 мм. Общая длина детали 90 мм. Шероховатость всех поверхностей со - ответствует параметру Да)2,5.

Упражнение 39. Выполните комплексные чер­тежи и аксонометрические проекции следующих геометрических тел:

]) цилиндра высотой 90 мм и диаметром 60 мм;

2) конуса высотой)00 мм и диаметром 50 мм;

3) куба со стороной ПО мм (М):2);

4) правильной треугольной призмы высотой 60 мм и стороной основания 45 мм;

5) правильной шестиугольной призмы высо­той)20мм и стороной основания 50 мм (М):2):

6) правильной четырехугольной пирамиды высотой 30 мм и стороной основания 20 мм (М 2:)). Нанесите размеры.

§ 28. ВСПОМОГАТЕЛЬНАЯ

ПРЯМАЯ КОМПЛЕКСНОГО

ЧЕРТЕЖА

. На чертеже, представленном на рис. ИЗ,' а, проведены оси проекций, а изобра­жений соединены между собой линиями связи. Горизонтальная и профильная про­екции соединены линиями связи с по­мощью дуг с центром в точке О пересече­ния осей. Однако в практике применяют и другое выполнение, комплексного черте­жа.

На безосных чертежах изображения располагают также в проекционной связи. Однако третья проекция может быть поме щена ближе или дальше. Например, про - фильная проекция может быть размещена правее (рис.! б. //)- или левее (рис.))3, б. /). Это важно для экономии места и удобства нанесения размеров.

Если на чертеже, выполненном по безос - ной системе, требуется провести между видом сверху и видом слева линии связи.

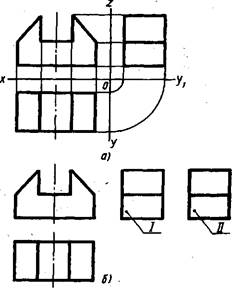Рис. ИЗ. Расположение проекций па чертеже

слш

я

8)

а)

ш

 

' 5)

ш й

 

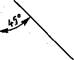
Рис. Н4. Использование вспомогательной прямой

& а)	^^^^ 6)
г)	д)	сквозное g)

Рис.)!5. Задания на построение прямоугольных проекций по наглядным изображениям

 

3 Техническое черчение 65

то применяют вспомогательную прямую комплексного чертежа. Для этого пример­но на уровне вида сверху и немного правее его проводят прямую под углом 45° к рам­ке чертежа (рис. 1)4, а). Она называется вспомогательной прямой комплексного чертежр. Порядок построения чертежа с помощью этой прямой показан на рис. 114, б, а.