Изучение двоично-кодированного параллельного счетчика

Цель работы: изучение двоично-кодированного параллельного счетчика, способов его проектирования, синтез двоично-кодированного параллельного счетчика как автомата Мура.

Краткие теоретические сведения. При каноническом методе синтеза счетчик представляется в виде автомата Мура без входных сигналов (рис. 6.1). Такой автомат состоит из комбинационной схемы (КС) и памяти. В качестве памяти выступают триггеры (). На информационные входы триггеров с выхода КС подаются функции возбуждения (ФВ) , которые переводят триггер в новое состояние 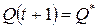. Выходы 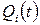триггеров определяют текущее состояние автомата. Выходы 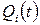через обратную связь подаются на входы КС. Выходы 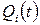определяют текущее значение двоично‑кодированного счетчика. Тактирование счетчика осуществляется при помощи импульсов синхронизации .

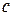Рис. 6.1. Представление счетчика в виде модификации автомата Мура

Исходные данные: приведены в табл. 6.1.

Подготовка к работе: перед выполнением работы изучить теоретический материал по литературе и лекциям, выполнить пункты 1 – 6 задания для получения допуска к выполнению лабораторной работы.

Задание:

1) построить совмещенную таблицу переходов и выходов двоично‑кодированного счетчика с заданным максимальным значением ;

2) найти СовДНФ или СовКНФ функций возбуждения триггеров счетчика;

3) с помощью карт Карно найти МДНФ или МКНФ функций возбуждения триггеров счетчика;

4) построить в универсальном базисе логическую схему двоично‑кодированного параллельного счетчика.

5) построить временные диаграммы работы двоично‑кодированного параллельного счетчика;

6) написать программу на языке VHDL, реализующую требуемый двоично‑кодированный параллельный счетчик в универсальном базисе;

7) провести моделирование счетчика в HDL Bencher;

8) получить конфигурационную последовательность проекта, реализующего двоично‑кодированный параллельный счетчик для конкретной микросхемы ПЛИС, и посмотреть ее в редакторе связей Floorplanner.

Таблица 6.1. Варианты заданий для построения двоично‑кодированного параллельного счетчика

№ варианта	Количество разрядов	Вид счета	Макс. значение	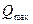Тип триггера	Вид миним. формы
		Прямой			ДНФ
		Прямой		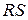	ДНФ
		Прямой		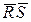	КНФ
		Обратный			ДНФ
		Обратный		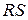	ДНФ
		Обратный		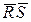	КНФ
		Прямой			КНФ
		Прямой		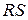	КНФ
		Прямой			ДНФ
		Обратный			КНФ
		Обратный		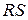	КНФ
		Обратный			ДНФ
		Прямой			ДНФ
		Прямой		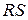	ДНФ
		Прямой			КНФ
		Прямой		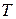	ДНФ
		Обратный		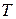	КНФ
		Обратный			КНФ
		Обратный			КНФ
		Обратный		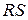	КНФ

Содержание отчета:

1) название, цель работы, задание;

2) проектирование схемы в соответствии с планом задания (п.п. 1 – 6 задания);

3) результаты моделирования схемы двоично‑кодированного параллельного счетчика в схемотехническом редакторе.

Пример выполнения работы.

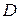Исходные данные: количество разрядов – 3, вид счета – прямой, =4, тип триггера – , вид минимальной формы – ДНФ.

1‑й этап. Построение совмещенной таблицы переходов и выходов двоично‑кодированного параллельного счетчика (табл. 6.2).

2‑й этап. Нахождение СовДНФ неполностью определенных ФВ (по табл. 6.2):

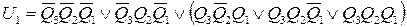, (6.1)

, (6.2)

. (6.3)

В выражениях (6.1) – (6.3) в скобках приведены наборы, соответствующие неопределенным выходным значениям.

Таблица 6.2. Совмещенная таблица переходов и выходов двоично‑кодированного параллельного счетчика, построенного на основе 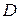‑триггеров (при )

Текущее состояние	Следующее состояние	Функции возбуждения
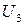
			X	X	X	X	X	X
			X	X	X	X	X	X
			X	X	X	X	X	X

3‑й этап. Нахождение МДНФ ФВ двоично‑кодированного параллельного счетчика с помощью карт Карно (рис. 6.2):

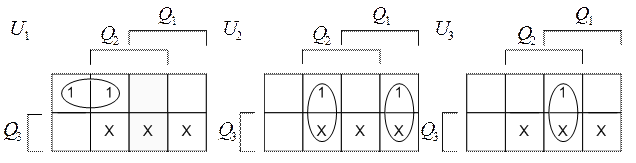
Рис. 6.2. Карты Карно для нахождения МДНФ ФВ (4.1) – (4.3)

Согласно рис. 6.2 ФВ 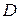‑триггеров счетчика в МДНФ примут вид:

, (6.4)

, (6.5)

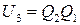. (6.6)

4‑й этап. Построение ЛС двоично‑кодированного счетчика (рис. 6.3) в универсальном базисе на основе полученных ФВ (6.4) – (6.6).

5‑й этап. Построение временных диаграмм (рис. 6.4) для синтезированного двоично‑кодированного параллельного счетчика.

6‑й этап. Написание программы на языке VHDL, реализующей двоично‑кодированный параллельный счетчик.

Следует отметить, что для вариантов заданий, в которых используются триггеры типов , , 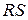и 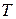, необходимо при реализации счетчика на языке VHDL запрограммировать заданный триггер на основе 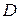‑триггера (как это делалось в лабораторной работе № 5). Вариант реализации 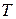‑триггера на основе 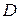‑триггера показан в примере выполнения лабораторной работы № 5.

Рис. 6.3. Двоично‑кодированный параллельный счетчик

Рис. 6.4. Временные диаграммы работы параллельного счетчика (см. рис. 6.3)

library IEEE;

use IEEE.STD_LOGIC_1164.ALL;

use IEEE.STD_LOGIC_ARITH.ALL;

use IEEE.STD_LOGIC_UNSIGNED.ALL;

 

entity lab6_vhdl_tbw is

Port (c: in std_logic;

Q: out std_logic_vector(3 downto 1));

end lab6_vhdl_tbw;

 

architecture Behavioral of lab6_vhdl_tbw is

 

SIGNAL U: STD_LOGIC_VECTOR(3 DOWNTO 1);

SIGNAL Q_IN: STD_LOGIC_VECTOR(3 DOWNTO 1);

 

begin

 

Q <= Q_IN;

 

U(1) <= (NOT Q_IN(3)) AND (NOT Q_IN(1));

U(2) <= (Q_IN(2) AND (NOT Q_IN(1))) OR (Q_IN(1) AND (NOT Q_IN(2)));

U(3) <= Q_IN(2) AND Q_IN(1);

 

PROCESS(c)

BEGIN

IF (c='1' AND c'EVENT) THEN

Q_IN <= U;

END IF;

END PROCESS;

 

end Behavioral;

7‑й этап. Моделирование работы параллельного счетчика в HDL Bencher (рис. 6.5).

 

Рис. 6.5. Результаты моделирования параллельного счетчика в HDL Bencher

8‑й этап. Получение конфигурационной последовательности T ‑триггера для конкретной микросхемы ПЛИС и просмотр размещения проекта внутри микросхемы в редакторе связей Floorplanner (рис. 6.6).

Рис. 6.6. Результаты размещения параллельного счетчика в микросхеме XC2V40-4-CS144 (фрагмент)

 

 

Контрольные вопросы:

1. Особенности минимизации неполностью определенных ПФ.

2. Построить совмещенную таблицу переходов и выходов заданного двоично‑кодированного счетчика с учетом заданного элемента памяти.

3. Найти МДНФ и МКНФ функций возбуждения заданного счетчика.

4. Построить схему заданного параллельного счетчика в универсальном базисе.

5. Преобразовать ФВ из универсального базиса в базисы Пирса и Шеффера.

6. Построить схему заданного параллельного счетчика в базисах Пирса и Шеффера.

 

Лабораторная работа № 7