Найти уравнение регрессии означает по эмпирическим данным математически описать изменения взаимно корреляционных величин, т.е. уравнение регрессии должно определить каким будет среднее значение результативного признака y при том или ином значении факторного признака x, если не учитывать остальные факторы, влияющие на y и не связанные с x. Рассчитанные по уравнению регрессии значения результативного признака наз-ся теоретическими и обозначаются 
или 
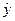. Читается: y выровненный по x. Для аналитической связи x и y могут использоваться следующие типы уравнений: 
(1)
Выбрав по эмпирическим данным тип функции, далее необходимо определить параметры а0, а1, а2 и т.д.
Парная регрессия представляет собой регрессию между двумя переменными– y и x, т. е. модель вида: ^y= f (x),
где y – зависимая переменная(результативный признак); x – независимая, или объясняющая, переменная (признак-фактор). Знак «^» означает, что между переменными x и y нет строгой функциональной зависимости, поэтому практически в каждом отдельном случае величина y складываетсяиз двух слагаемых: ^y= yх +ε, где y – фактическое значение результативного признака; ^ yх – теоретическое значение результативного признака, найденное исходя из уравнения регрессии; ε – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина ε называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками:
спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака ^y x, подходят к фактическим данным y.
Регрессия - величина, выражающая завис-ть среднего значения случ. величины у от значений случ.величины х.
Интерпретация моделей регрессии осущ-ся методами той отрасли знаний, к кот. относится исследуемое явление. Но всякая интерпретация начинается со статистической оценки уравн-ия регрессии в целом и оценки значимости входящих в модель факторных признаков.
Прежде всего необходимо рассмотреть коэффициенты регрессии. Чем больше величина коэфф-та регрессии, тем значительнее влияние данного признака на моделируемый. Знаки коэфф. регрессии говорят о характере влияния на результативный признак. Если факторный признак имеет знак +, то с увеличением данного фактора результативный признак возрастает; если факторный признак имеет знак -, то с его увеличением результативный признак уменьшается.
Парная регрессия.
Парной регрессией называется уравнение связи двух переменных у и х Вида y = f (x),где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических значений ŷx при тех же значениях фактора x минимальна