Дифференциальные уравнения первого порядка

И методы их решения

Математическое описание самых разнообразных процессов, происходящих в природе, часто приводит к уравнениям, связывающим:

1) независимую переменную;

2) искомую функцию;

3) производные этой функции.

Такого рода уравнения называются дифференциальными.

Пусть

В приложениях математики к техническим наукам дифференциальные уравнения занимают особо важное место. Многие прикладные процессы с их помощью описываются проще и полнее.

Дифференциальные уравнения дают возможность решать многие задачи физики, теоретической механики, сопротивления материалов, гидравлики, ТММ, химии, технологии производств, биологии, финансово-политических дисциплин и др. – и возникают при решении этих задач.

Поэтому вполне понятно то внимание, которое должно быть уделено курсу составления дифференциальных уравнений.

Вначале составляется дифференциальное уравнение задачи, которое затем решается тем или иным способом (в зависимости от типа уравнения).

В зависимости от условия задачи дифференциальное уравнение получается:

1) либо как соотношение между дифференциалами переменных величин;

2) либо как соотношение, содержащее производные неизвестной функции.

При составлении дифференциального уравнения задачи используется геометрический или механический смысл производной.

Кроме того, при составлении дифференциального уравнения задачи, в зависимости от ее условия, используются известные законы физики, механики и других наук и различные математические сведения.

Сначала рассмотрим задачи геометрического и физического характера, приводящие в процессе своего решения к дифференциальным уравнениям.

Задача 1. Найти уравнение кривой зная, что длина отрезка, отсекаемого касательной в произвольной точке кривой на оси ординат, равна удвоенной ординате точки касания, известно что искомая линия проходит через точку (1;2).

Решение.

В

М(х;у)

А

Возьмем на искомой кривой произвольную точку М (х; у). Уравнение касательной в точке М имеет вид:

где Х,У - текущие координаты точек касательной;

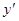- производная искомой функции в данной точке М.

Для нахождения длины отрезка ОВ, отсекаемого касательной на оси Оу, положим Х=0. Тогда . С другой стороны, по условию ОВ=2у. Сравнивая оба выражения для ОВ, получаем уравнение:

. (1)

Это и есть дифференциальное уравнение задачи. Заменим 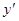на : , или - это и есть равенство дифференциалов двух следующих выражений:

Но из дифференциального исчисления известно, что если дифференциалы двух функций равны, то сами функции отличаются друг от друга лишь на постоянное слагаемое.

Поэтому имеем:

Можно так: , заменим . Левая часть представляет собой дифференциал произведения переменных , поэтому последний можно записать в виде , откуда , где С - произвольное постоянное.

Уравнение кривой можно записать в явном виде:

Это уравнение представляет собой, собственно, не одну кривую, а целое семейство кривых (линий – семейство гипербол, асимптотами которых служат координатные оси.).

Из полученного семейства выделим теперь искомую линию, проходящую через точку (1;2):

Ответ:

Задача 2. Материальная точка массой в 1 грамм движется прямолинейно под действием силы, прямо пропорциональной времени (время отсчитывается от момента t=0) и обратно пропорциональной скорости движения точки. Найти формулу для скорости движения материальной точки, если известно, что в момент времени t=10 сек скорость была равна 50см/сек, а сила равна 4 динам.

Решение. Величина действующей силы (1), где к - коэффициент пропорциональности. Известно, что при t=10cек, v=50см/сек, F=4динм. Из этих данных найдем к: к=20

По второму основному закону динамики (второй закон Ньютона) F=ma.

Известно, что ускорение движения есть производная от скорости по времени:

Подставим в (1): , или это и есть дифференциальное уравнение движения точки. Уравнение этом можно записать в виде

Это и есть равенство дифференциалов двух следующих выражений:

Но известно, что если дифференциалы двух функций равны, то сами функции отличаются друг от друга разве лишь на постоянное слагаемое

(произвольную постоянную взяли так для удобства записи)

- это и есть искомая формула.

Найдем С: при t=10,v=50 .

Ответ:

Задача 3. Материальная точка массы свободно падает под действием силы тяжести. Найти закон движения точки без учета сопротивления воздуха.

Решение. Возьмем вертикальную ось, направленную вниз, с выбранной на ней точкой отсчета О. Положение материальной точки определится координатой S=OM, изменяющейся в зависимости от времени t. На точку действует только сила тяжести P=mg, где g - ускорение силы тяжести. По второму основному закону динамикки .

Получаем 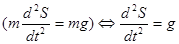- это и есть дифференциальное уравнение, содержащее вторую производную неизвестной функции S=S(t). Искомую функцию S(t) легко получить, произведя дважды интегрирование по t. Последовательно находим: . Равенство (2) дает искомый закон движения, однако, как и в предыдущих задачах, оно содержит постоянные интегрирования, в данной задаче - две. Их можно определить, зная начальное положение и начальную скорость точки.

Пусть в начальный момент t=0 скорость точки равна , а ее расстояние от точки отсчета О равно . Из (1) получаем: , а из (2): . И закон движения приобретает вид: .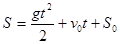

Основные понятия

Теперь можно перейти к определению основных понятий.

Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков.

Примерами дифференциальных уравнений являются уравнения, полученные в ходе решения задач 1-3. Во всех этих уравнениях неизвестная функция является функцией одного аргумента. Такие уравнения называют обыкновенными дифференциальными уравнениями в отличие от уравнений с частными производными, в которых рассматриваются неизвестные функции, зависящие от нескольких аргументов.

Мы будем рассматривать только обыкновенные дифференциальные уравнения.

Определение 2. Порядком дифференциального уравнения называется порядок входящей в уравнение старшей производной (или дифференциала).

Так, уравнения в задачах 1-2 являются уравнениями первого порядка, а уравнение в задаче 3 – второго порядка, так как содержит вторую производную.

Пример: уравнение - уравнение первого порядка;

Уравнение - уравнение второго порядка.

Порядком дифференциального уравнения неизвестной величиной является функция, входящая в уравнение вместе с некоторыми своими производными.

Определение 3. Любая функция , которая удовлетворяет данному дифференциальному уравнению, т.е. обращает его в тождество при замене y и его производных на и ее производные, называется решением дифференциального уравнения.

Если функция, удовлетворяющая уравнению, задана соотношением вида или параметрически, то говорят об интеграле уравнения.

Приведенные выше примеры показывают, что одному и тому же уравнению удовлетворяют, вообще говоря, многие функции, так что для выделения одной из них необходимо задание дополнительных условий.

Дифференциальные уравнения первого порядка