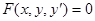(1)
Обычно уравнение (1) стараются представить в форме, разрешенной относительно производной:
(2)
Или в форме, содержащей дифференциалы:
(3)
Замечание. От формы (2) легко перейти к форме (3) и наоборот. Как уже было сказано, дифференциальному уравнению удовлетворяет, вообще говоря, целая система функций. Для выделения одной из них следует указать ее значение при каком-либо значении аргумента, т.е. задать условие вида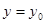 
при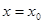 
, которое называется начальным условием. Часто его записывают в виде 
(4)
Определение 1. Решение 
(или интеграл 
) дифференциального уравнения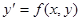 
, удовлетворяющее условию (4) (если это решение существует), называется частным решением (или частным интегралом) дифференциального уравнения, удовлетворяющим заданному начальному условию.
Например, решение 
есть частное решение дифференциального уравнения 
, удовлетворяющее начальному условию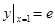 
.
Определение 2. Решение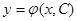 
(или интеграл 
) дифференциального уравнения (2), зависящего от произвольной постоянной С, называется общим решением (или общим интегралом) дифференциального уравнения (2), если путем подбора значений произвольной постоянной из него можно получить частное решение (частный интеграл), удовлетворяющее любому возможному начальному условию
Практически для определения С следует подставить в общее решение (общий интеграл) вместо х и у заданные значения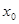 
и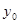 
разрешить уравнение 
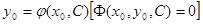относительно неизвестного С. Пусть 
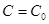, тогда частное решение будет 
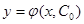(соответственно частный интеграл 
).
Геометрический смысл решений дифференциального уравнения первого порядка
При геометрическом истолковании дифференциального уравнения приходится рассматривать график его решения, который называют интегральной кривой уравнения.
Пусть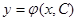 
- общее решение дифференциального уравнения .
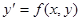Придавая С различные значения, будем получать из общего решения соответствующие частные решения 
, и т.д., которые будут изображаться на плоскости интегральными кривыми. Следовательно,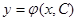 
- уравнение семейства интегральных кривых, зависящих от параметра С. Таким образом, геометрически общее решение представляет собой семейство интегральных кривых, зависящих от одного параметра С. Частное решение есть одна из интегральных кривых этого семейства, проходящая через точку 
.
Геометрический смысл дифференциального уравнения, разрешенного относительно производной
Дифференциальное уравнение 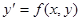(2) может быть истолковано геометрически следующим образом. Пусть 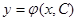есть общее решение этого уравнения, т.е. семейство интегральных кривых в некоторой области Д плоскости Оху, в которой определена функция 
. Уравнение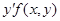 
(2) устанавливает связь между координатами любой точки М(х,у) 
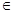Д и значением производной в этой точке.
Задавая координаты х и у точки М, можно из уравнения (2) найти значение производной, т.е. угловой коэффициент касательной касательной к интегральной кривой, проходящей через точку М.
Таким образом, дифференциальное уравнение (2) определяет совокупность направлений или, как говорят, поле направлений в области Д.
Изображая направление в каждой точке области Д маленькой стрелкой, выходящей из этой точки, можно построить поле направлений дифференциального уравнения (2).
у
0 х
Операцию отыскания решений дифференциального уравнения часто называют интегрированием уравнения, т.к. в ряде случаев решение дифференциальных уравнений сводится к интегрированию функций.
Геометрически задача интегрирования дифференциального уравнения (2) заключается в нахождении кривых, которые в каждой своей точке касаются направления задаваемого полем.
В каких случаях можно гарантировать, что решение, удовлетворяющее данным начальным условиям, действительно существует и когда можно быть уверенным, что такое решение только одно? Другими словами, возникает вопрос об условиях существования частного решения, удовлетворяющего данному начальному условию. Наиболее простые из них даются следующие теоремой теоретического существования и единственности решения дифференциального уравнения первого порядка.
Теорема Коши. Если функция определена и непрерывна в области Д плоскости Оху и имеет непрерывную частную производную 
во всех точках этой области, то, какова бы ни была точка 
, всегда существует, и притом единственная, функция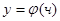 
, которая определена и непрерывна в некотором интервале, содержащем точку 
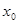, является решением уравнения 
и принимает при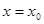 
значение 
.
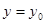Геометрически это означает, что через любую точку 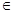Д проходит единственная интегральная кривая, т.е. кривая, в каждой своей точке касающаяся направления, задаваемого полем, которое определяется дифференциальным уравнением.